Минимизация логических функций. Метод диаграмм Вейча.

1. Переменная х_i является несущественной переменной, если при изменении ее значения на противоположное функция остается прежней:

_

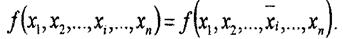
2. Склеивание: x_i V x_i = 1.

1). Для двух переменных

Склеиваются те клетки, которые имеют рядом стоящие единицы.

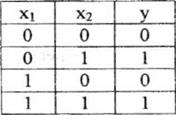
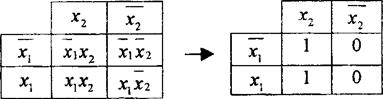
Диаграмма Вейча Результат склеивания

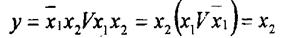
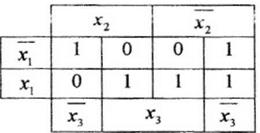
2). Для трех переменных

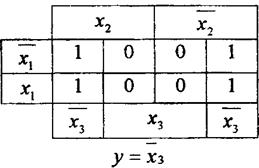
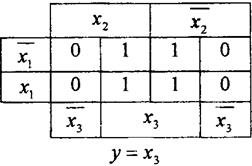
Если в диаграмме Вейча рядом стоит четыре единицы, то такое склеивание приводит к зависимости от одной переменной.

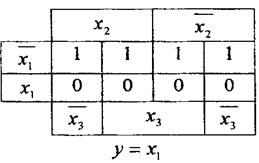
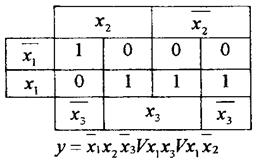
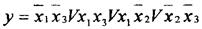
3). Для четырех переменных

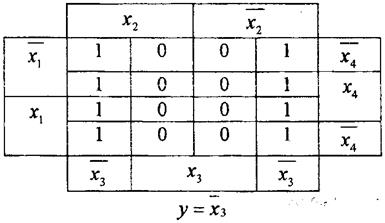
Если рядом стоят восемь единиц, то функция зависит от одной переменной, четыре - от двух, две - от трех.

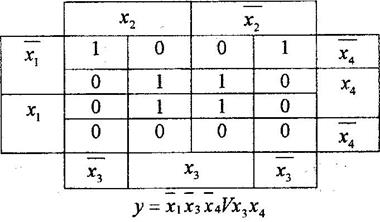
Диаграммы Вейча удобно использовать для не полностью определенных функций.

Пример

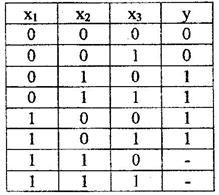
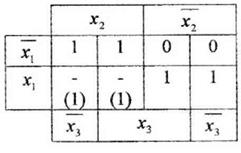
Вместо неопределенных значений функции поставим, где это удобно, единицы для того, чтобы склеить их как можно больше. Получим конечную функцию: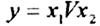

Примечание: в реальных схемах не полностью заданные функции получаются тогда, когда некоторые комбинации двоичных входов являются запрещенными, либо они не могут быть поданы на вход схемы в силу особенностей работы логического элемента.