Свойства определителей. 1.Определитель не меняется при транспонировании матрицы.

1.Определитель не меняется при транспонировании матрицы.

2.Если одна из строк (один из столбцов) определителя состоит из нулей, то определитель равен нулю.

3.Определитель, содержащий две одинаковые строки (столбца), равен нулю.

4.Определитель, содержащий две пропорциональные строки (столбца), равен нулю.

5.При перестановке двух строк (столбцов) определитель меняет знак на противоположный.

6.Общий множитель элементов любой строки (столбца) можно вынести за знак определителя.

7.Величина определителя не изменится, если к одной из его строк (столбцов) прибавить другую строку (столбец), умноженную на какое угодно число.

Пример 7. Вычислить определитель .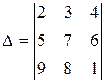

Решение.

Вычислим этот определитель, разложив его по элементам третьего столбца.

Для того чтобы упростить вычисления сделаем следующие преобразования: умножим третью строку на “-6” и прибавим ее ко второй строке ( 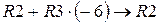); умножим третью строку на “-4” и прибавим ее к первой строке ( ):

.

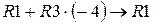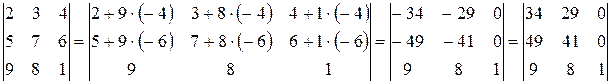Разложим определитель по элементам третьего столбца:

.

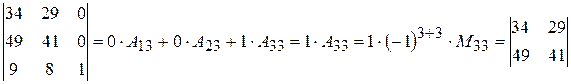Вычтем второй столбец из первого столбца ( ):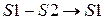

.

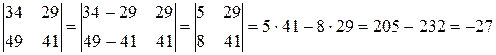Обратная матрица