Основные уравнения электростатики диэлектриков

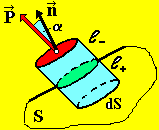Рис. 4

Пусть произвольная замкнутая поверхность S охватывает некоторую часть изотропного диэлектрика.

При внесении диэлектрика во внешне электростатическое поле он поляризуется. Найдем заряд, который проходит через малый элемент dS замкнутой поверхности S (рис. 4).

Есл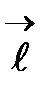и ₊ и 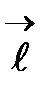_- - векторы, характеризующие смещение положительного и отрицательного связанных зарядов, то через элемент поверхности dS наружу поверхности S выйдет положительный заряд dq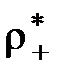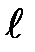₊^* = ₊dSсosa.

Согласно закону сохранения заряда одновременно через элемент dS внутрь поверхности S войдет отрицательный заряд dq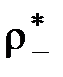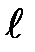_-^*= _-dSсosa. Тогда суммарный связанный заряд, выходящий наружу поверхности S через элемент dS,

dq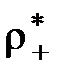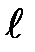^*= ₊dSсosa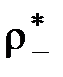+½ ½ 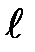_-dScosa.

С учетом того, что 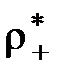=½ 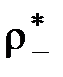½,для суммарного заряда получим

dq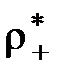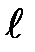^*= dScosa, (8)

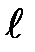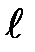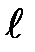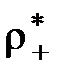
где = ₊ + _- - расстояние, на которое сместились положительные и отрицательные связанные заряды изотропного диэлектрика друг относительно друга при поляризации. Поскольку = 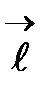- дипольный момент единицы объема диэлектрика, или Р =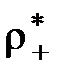 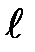и dq^* = PdSсosa, то суммарный связанный заряд

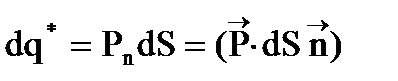. (9)

Скалярное произведение в формуле (6.9) является элементарным потоком вектора сквозь произвольную замкнутую поверхность.

Интегрируя выражение (9) по всей замкнутой поверхности S, найдем полный заряд, который вышел при поляризации из объема, охватываемого этой поверхностью, т. е.

q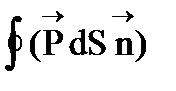^* = = -q^*. (10)

Внутри замкнутой поверхности S останется избыточный связанный заряд q^*. Таким образом, вышедший заряд равен оставшемуся внутри поверхности S избыточному связанному заряду с обратным знаком.

Вывод: Поток вектора сквозь произвольную замкнутую поверхность равен взятому с обратным знаком избыточному связанному заряду диэлектрика в объеме, охватываемом этой поверхностью, т. е.

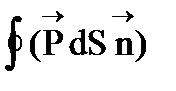= -q^*. (11)

Следовательно, формула (11) выражает теорему Гаусса для вектора поляризации .

В дифференциальной форме теорема Гаусса для вектора поляризации записывается в виде

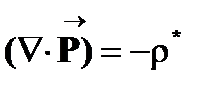, (12)

т. е. дивергенция поля вектора равна с обратным знаком объемной плотности избыточного связанного заряда.

Замечание: объемная плотность избыточных связанных зарядов внутри диэлектрика равна нулю при одновременном выполнении следующих условий:

1) внутри диэлектрика не должно быть сторонних зарядов (r = 0);

2) диэлектрик должен быть изотропным и однородным.