Производственная функция, ее основные свойства

Производством называется любая человеческая деятельность по преобразованию ограниченных ресурсов – материальных, трудовых, природных — в готовую продукцию. Производственная функция характеризует зависимость между количеством используемых ресурсов (факторов производства) и максимально возможным объемом выпуска, который может быть достигнут при условии, что все имеющиеся ресурсы используются наиболее рациональным образом.

Производственная функция обладает следующими свойствами:

1 Существует предел увеличения производства, который может быть достигнут при увеличении одного ресурса и постоянстве прочих ресурсов. Если, например, в сельском хозяйстве увеличивать количество труда при постоянных количествах капитала и земли, то рано или поздно наступает момент, когда выпуск перестает расти.

2 Ресурсы дополняют друг друга, но в определенных пределах возможна и их взаимозаменяемость без сокращения выпуска. Ручной труд, например, может заменяться использованием большего количества машин, и наоборот.

Производство не может создавать продукцию из ничего. Процесс производства связан с потреблением различных ресурсов. В число ресурсов входит все то, что необходимо для производственной деятельности, – и сырье, и энергия, и труд, и оборудование, и пространство.

Для того чтобы описать поведение фирмы, необходимо знать, какое количество продукта она может произвести, используя ресурсы в тех или иных объемах. Мы будет исходить из допущения, что фирма производит однородный продукт, количество которого измеряется в натуральных единицах - тоннах, штуках, метрах и т. д. Зависимость количества продукта, которое может произвести фирма, от объемов затрат ресурсов получила название производственной функции.

Но предприятие может по-разному осуществить производственный процесс, используя разные технологические способы, разные варианты организации производства, так что и количество продукта, получаемое при одних и тех же затратах ресурсов, может быть разным. Руководители фирмы должны отклонить варианты производства, дающие меньший выход продукта, если при тех же самых затратах каждого вида ресурса можно получить больший выход. Точно так же они должны отклонить варианты, требующие больших затрат хотя бы одного ресурса без увеличения выхода продукта и сокращения затрат других ресурсов. Варианты, отклоняемые по этим соображениям, носят название технически неэффективных.

Допустим, ваша фирма производит холодильники. Для изготовления корпуса нужно раскроить листовое железо. В зависимости от того, как будет размечен и раскроен стандартный лист железа, из него можно вырезать больше или меньше деталей; соответственно для изготовления определенного количества холодильников потребуется меньше или больше стандартных листов железа. При этом расход всех остальных материалов, труда, оборудования, электроэнергии останется без изменения. Такой вариант производства, который может быть улучшен путем более рационального раскроя железа, должен быть признан технически неэффективным и отклонен.

Технически эффективными называют варианты производства, которые нельзя улучшить ни увеличением производства продукта без увеличения расхода ресурсов, ни сокращением затрат какого-либо ресурса без снижения выпуска и без увеличения затрат других ресурсов. Производственная функция учитывает только технически эффективные варианты. Ее значение – это наибольшее количество продукта, которое может произвести предприятие при данных объемах потребления ресурсов.

Рассмотрим вначале простейший случай: предприятие производит единственный вид продукции и расходует единственный вид ресурса. Пример такого производства довольно трудно найти в действительности. Даже если рассмотреть предприятие, оказывающее услуги на дому у клиентов без применения какого-либо оборудования и материалов (массаж, репетиторство) и затрачивающее только труд работников, нам пришлось бы допустить, что работники обходят клиентов пешком (не используя услуг транспорта) и договариваются с клиентами без помощи почты и телефона.

Производственная функция – показывает зависимость количества продукта, которое может произвести фирма, от объемов затрат используемых факторов

Q = f (x1, x2…xn)

Q = f (K, L),

где Q - объем выпуска

x1, x2…xn – объемы применяемых факторов

K- объем капитального фактора

L - объем трудового фактора

Итак, предприятие, затрачивая ресурс в количестве х, может произвести продукт в количестве q. Производственная функция

устанавливает связь между этими величинами. Заметим, что здесь, как и в других лекциях, все объемные величины – это величины типа потока: объем затрат ресурса измеряется количеством единиц ресурса в единицу времени, а объем выпуска - количеством единиц продукта в единицу времени.

Производственная функция вида (30.1), устанавливающая зависимость объема производства от объема затрат единственного ресурса, может использоваться не только в иллюстративных целях. Она полезна и тогда, когда может изменяться расход лишь одного ресурса, а затраты всех остальных ресурсов по тем или иным причинам должны рассматриваться как фиксированные. В этих случаях интерес представляет зависимость объема производства от затрат единственного переменного фактора.

Значительно большее разнообразие появляется при рассмотрении производственной функции, зависящей от объемов двух потребляемых ресурсов:

Приведенная производственная функция говорит о том, что производитель может заменять труд капитаном и капитал трудом, оставляя выпуск неизменным. Например, в сельском хозяйстве развитых стран труд является высокомеханизированным, т.е. на одного работника приходится много машин (капитала). Напротив, в развивающихся странах тот же объем производства достигается за счет большого количества труда при незначительном капитале. Это позволяет построить изокванту (рис. 30.1).

Изокванта (линия равного продукта) отражает все комбинации двух факторов производства (труда и капитала), при которых выпуск остается неизменным. На рис. 30.1 рядом с изоквантой проставлен соответствующий ей выпуск. Так, выпуск 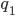, достижим при использовании 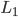труда и 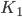капитала или с использованием 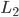труда и капитана. Производители также являются потребителями, используя ресурсы: капитал и работников. Для исследования их поведения в данном случае также используются кривые безразличия – изокванты (isoquant) или линии равного продукта и бюджетные линии – изокосты (isocost) или линии равных затрат рис. 30.2.

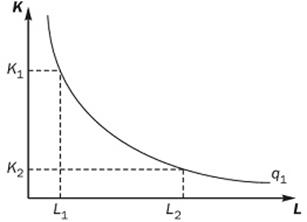
Рисунок. 30.1 – Изокванта

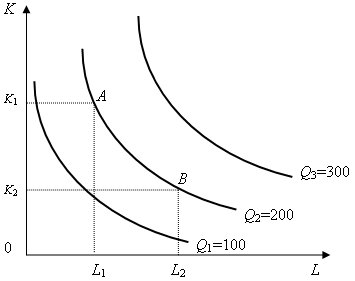
Рисунок 30.2 – Изокванты, представляющие разные уровни выпуска. К – производственный капитал (оборудование); L – число рабочих

Для фирмы изокванты – это кривые равных полезностей, но в отличие от кривых безразличия они показывают реальные объемы производства.

Совокупность изоквант, каждая из которых показывает максимальный выпуск продукции, достигаемый при использовании определенных комбинаций ресурсов, называется картой изоквант. Чем дальше от начала координат расположена изокванта, тем больший объем продукции она представляет.

Возможны и другие комбинации объемов труда и капитала, минимально необходимых для достижения данного выпуска.

Все комбинации ресурсов, соответствующих данной изокванте, отражаюттехнически эффективные способы производства. Способ производства A является технически эффективным в сравнении со способом В, если он требует использования хотя бы одного ресурса в меньшем количестве, а всех остальных не в больших количествах в сравнении со способом В. Соответственно способ В является технически неэффективным в сравнении сА. Технически неэффективные способы производства не используются рациональными предпринимателями и не относятся к производственной функции.

Из вышесказанного вытекает, что изокванта не может иметь положительный наклон, как это показано на рис. 30.3.

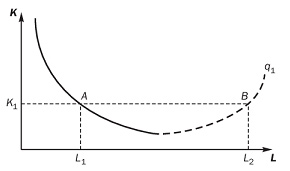
Рисунок. 30.3 – Технически эффективное и неэффективное производство

Отрезок, выделенный пунктиром, отражает все технически неэффективные способы производства. В частности, в сравнении со способомА способВ для обеспечения одинакового выпуска ( 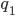) требует того же количества капитала, но большего количества труда. Очевидно, поэтому, что способ B не является рациональным и не может приниматься в расчет.

На основе изокванты можно определить предельную норму технической замены.

Предельная норма технической замены фактора Y фактором X (MRTS_XY) — это количество фактора 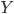(например, капитала), от которого можно отказаться при увеличении фактора 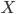(например, труда) на 1 ед., чтобы выпуск не изменился (остаемся на прежней изокванте).

На изокванте увеличение использования одного фактора (L) компенсируется уменьшением использования другого фактора (К). От скольких единиц одного фактора (К) можно отказаться для увеличения второго фактора (L) на единицу, показывает предельная норма технической замены – MRTS ф-ла 30.3:

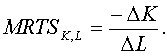(30.3)