Пример определения диапазона значений передаточного коэффициента управляющего устройства для устойчивой системы
Система автоматического управления представлена структурной схемой, приведенной на рисунке 63:
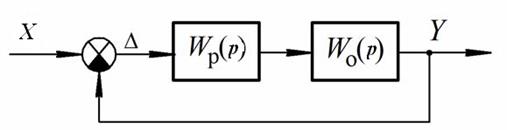
Рис.63. Структурная схема САУ
Требуется определить диапазон значений передаточного коэффициента kp управляющего устройства, при котором система будет устойчивой, при следующих параметрах:
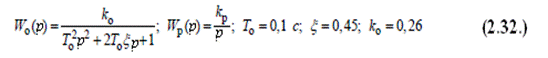
Решение:
Определим передаточную функцию всей системы:
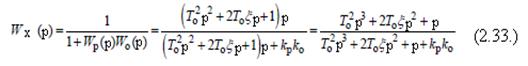
Заменим
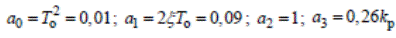 (2.34.)
(2.34.)
и получим характеристическое уравнение системы следующего вида:
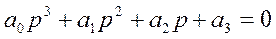 (2.35.)
(2.35.)
В соответствии с критерием Гурвица и рассмотренным Примером 1, для устойчивой системы, описываемой характеристическим уравнением третьего порядка справедливо неравенство:
a1a2 > a0a3 (2.36.)
поэтому подставив имеющиеся данные, получим:
a1a2 = 0,09 х 1 > 0,01 х 0,26kр = a0a3, где 0 < kр < 34,62 (2.37.)
Диапазон значений передаточного коэффициента управляющего устройства, при котором система будет устойчивой, найден.
Критерий Рауса
Практически одновременно с Гурвицем английский математик Э. Раус предложил свой алгебраический критерий устойчивости САУ, описываемых дифференциальными уравнениями n – ного порядка. Критерий Рауса сформулирован таким образом – система устойчива, если все коэффициенты первого столбца таблицы Рауса положительные. Если не все коэффициенты первого столбца положительные, то система неустойчива, а количество положительных корней характеристического уравнения равно числу перемен знака в первом столбце таблицы.
При составлении таблицы Рауса применяются следующие правила:
- В первой строке таблицы необходимо записать коэффициенты характеристического уравнения с четными индексами в порядке их возрастания.
- Во второй строке таблицы необходимо записать коэффициенты характеристического уравнения с нечетными индексами в порядке их возрастания
- Следующие строки таблицы заполняются по формуле:
ck,i = ck+ 1,i - 2 - ri  ck + 1,i – 1 , где ri = c1 ,i – 2 / c1,i – 1 , i
ck + 1,i – 1 , где ri = c1 ,i – 2 / c1,i – 1 , i  3 - номер строки,
3 - номер строки,
k - номер столбца.
- Строк в таблице на одну больше, чем порядок характеристического уравнения.
| Ri | i\k | ||||
| - | 1 | c11 = a0 | c21 = a2 | c31 = a4 | ... |
| - | 2 | c12 = a1 | c22 = a3 | c32 = a5 | ... |
| r3 = c11/cc12 | 3 | c13 = c21-r3c22 | c23 = c31-r3c32 | c33 = c41-r3c42 | ... |
| r3 = c11/c12 | 4 | c14 = c22-r3c23 | c24 = c32-r4c33 | c34 = c42-r4c43 | ... |
| ... | ... | ... | ... | ... | ... |
Рис.64. Образец заполнения таблицы Рауса
Достоинство критерия Рауса в простоте его использования независимо от порядка характеристического уравнения.
Недостаток критерия Рауса в его малой наглядности, трудности определения степени устойчивости системы, как далеко она находится от границы устойчивости.
Примеропределения устойчивости САУ по критерию Рауса
Необходимо определить устойчивость САУ, ее структурная схема на рисунке 65.
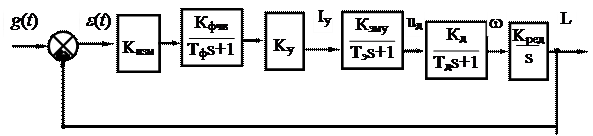
Рис.65. Структурная схема САУ
Обозначения в структурной схеме:
Кизм - передаточный коэффициент измерительного устройства; Кфчв, Тф – передаточный коэффициент и постоянная времени фазочувствительного выпрямителя; Ку - коэффициент усиления электронного усилителя; Кэму Тэ - коэффициент передачи и постоянная времени электромашинного усилителя; Кд, Тд - коэффициент передачи и постоянная времени электрического двигателя; Кред - коэффициент передачи редуктора.
| Кизм В/град | Кэму В /мА | Тфчв сек | Тэму сек | Кд | Тд сек | Кред | Кфчв | Ку |
| 2,0 | 0,004 | 0,015 | 2,15 | 0,3 | 0,003 |
Рис.66. Таблица числовых значений данных
Решение:
Найдем передаточную функцию системы:
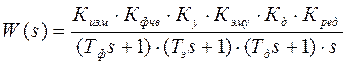
 (2.38.)
(2.38.)
Подставив числовые значения, получим:
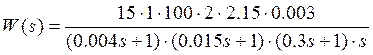 (2.39.)
(2.39.)
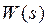
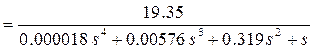
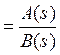 (2.40.)
(2.40.)
Получим представление характеристического полинома в следующем виде:
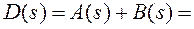
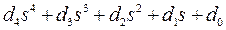 (2.41.)
(2.41.)
Характеристическое уравнение будет иметь вид:
D(s) = 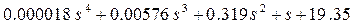 (2.42.)
(2.42.)
Составим таблицу Рауса в соответствии с правилами и получим:
| 0.000018 | 0.319 | 19.35 | |
| 0.00576 | |||
| r3 = 0.003125 | 0.315875 | 19.35 | |
| r4 = 0.018235 | 0.647152 | ||
| r 5 = 0.4881 | 19.35 |
Рис.67. Таблица Рауса
Из анализа таблицы следует, что коэффициенты первого столбца таблицы положительны, а значит, система устойчива.
Дата добавления: 2016-02-04; просмотров: 2217;
