Метод векторных диаграмм

Принцип Гюйгенса-Френеля

Любую плоскую электромагнитную волну можно представить в виде световых лучей, т. е. в виде узкого пучка света. В однородной среде свет распространяется прямолинейно, что подтверждается образованием тени от непрозрачных предметов. Любое отклонение при распространении волны от законов геометрической оптики называют дифракцией.

Благодаря дифракции световые волны (как и любые другие волны, например, акустические) могут попадать в область геометрической тени: огибать препятствия, распространяться вдоль поверхностей, проникать сквозь малые отверстия, размеры которых сравнимы или меньше длины волны.

Для объяснения дифракции света (волновая природа света) используют принцип Гюйгенса-Френеля: каждая точка фронта волны является источником вторичных волн, которые когерентны и интерферируют.

Принцип Гюйгенса-Френеля позволяет найти результирующую амплитуду в некоторой точке пространства. Согласно принципу Гюйгенса-Френеля свет должен наблюдаться в тех точках пространства, куда при интерференции вторичные волны приходят в одинаковой фазе (усиливают друг друга - максимум интерференции). В тех точках пространства, куда они приходят в противофазе (гасят друг друга - минимум интерференции), наблюдается темнота. Физический смысл огибающей вторичных волн заключается в том, что все вторичные волны колеблются в этот момент в одинаковых фазах и их интерференция приводит к максимальной интенсивности света. По этой причине и отсутствует обратная волна.

Действительно, вторичные волны, распространяющиеся вперед от волнового фронта, попадают в невозмущенное пространство. Они интерферируют только друг с другом. Вторичные волны, идущие назад, где распространяются в противофазе с ними первичные волны, гасят друг друга.

Метод зон Френеля

Строгий расчет дифракции света связан с математическими трудностями. Френель предложил более простой метод для объяснения дифракции света, который называют методом зон Френеля. Согласно этому методу в любой момент времени волновую поверхность S разбивают на отдельные зоны, каждая из которых отделена от предыдущей на l/2 (рис. 8.1). При распространении плоской монохроматической электромагнитной (световой) волны (параллельный пучок лучей) в т. М на экране наблюдается дифракция света в виде чередующихся светлых и темных колец.

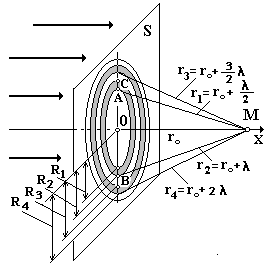Рис. 8.1

На произвольной волновой поверхности S, находящейся на расстоянии r₀ (ОМ) от экрана, выделим зоны, которые в данном случае, образуют ряд концентрических окружностей (колец). Границей первой (центральной) зоны служат точки поверхности S, находящейся на расстоянии r₁ = 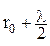от точки М (рис. 8.1).

Соответственно точки В, С волновой поверхности, находящиеся на

расстоянии r₁ = r₀+ l, r₃ = и т. д. от т. М, образуют границы второй, третьей и т.д. зон Френеля. Найдем радиусы зон Френеля. В D ОАМ радиус первой зоны

,

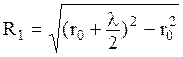т. е. 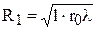, (8.1)

где r₀ - расстояние от т. О до т. М;

l - длина волны света.

В D ОВМ радиус второй зоны

или

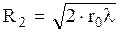, (8.2)

где слагаемым l² пренебрегаем, так как l² <<R. В D ОСМ радиус третьей зоны 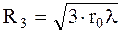и т. д. (8.3)

Следовательно, для любой m - й зоны Френеля

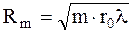, (8.4)

где m = 1, 2, 3, ... .

Используя (8.1), находим площадь первой зоны

S₁ = p 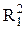= pr₀l. (8.5)

Все остальные зоны Френеля представляют собой концентрические полосы. Поэтому площадь второй зоны равна разности площадей круга радиуса R₂ и R₁, т. е.

S₂ = pR₂² - p R₁² = pr₀l. (8.6)

Площадь третьей зоны S₂ 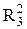= p - p 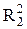= pr₀l и т. д.

Площадь m - ой зоны S_m = pr₀l. (8.7)

Таким образом, площади всех зон Френеля равновелики и содержат одинаковое количество вторичных источников.

Вторичные волны, возбуждаемые в т. М от двух соседних зон, противоположны по фазе и при наложении гасят друг друга. Так как оптическая разность хода d в т. М равна нечетному числу длин полуволн (условие минимума интерференции).

Следовательно, амплитуду результирующей волны можно найти по формуле А = А₁ - А₂ + А₃ - А₄ + ... , (8.8)

где А₁, А₂, А₃, ... – амплитуды волн, возбуждаемых в т. М 1-, 2-, 3-й и т. д. зонами Френеля.

Чередование знаков «±» вызвано тем, что соседние зоны гасят друг друга. Однако по мере увеличения номера зоны величина амплитуда волны от соответствующих зон уменьшается, т. е. А₁ > А₂ > А₃ > А₄ > ... . Общее число зон Френеля на волновом фронте велико (N » 10⁵). Результирующую амплитуду можно получить, если представить (8.8) в следующем виде

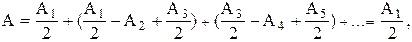(8.9)

так как все выражения, стоящие в скобках, равны нулю.

Следовательно, при полностью открытом фронте волны амплитуда результирующей волны равна половине амплитуды первой зоны Френеля.

Если свет распространяется от близкого точечного источника S (рис. 8.2, а, б), то применяя метод зон Френеля находим, что радиус m-й зоны

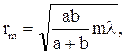(8.10)

где a – радиус волновой поверхности; b – расстояние от вершины волновой поверхности до экрана; m – номер зоны; l - длина волны света.

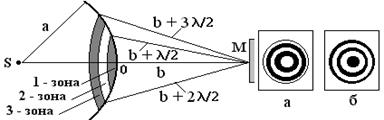Рис. 8.2

Волны, возбуждаемые в т. М любым четным числом зон, противоположны по фазе и при наложении гасят друг друга, т. е. в центре дифракционной картины наблюдается темное пятно (рис. 8.2, б). Если число зон нечетно, то в центре дифракционной картины наблюдается светлое пятно (рис. 8.2, а).

Если в формуле (8.2, а) положить a = b = 1 м и l = 500 нм, то радиус первой (центральной) зоны Френеля r₁ = 0,5 мм. Поэтому практически можно считать, что свет распространяется от точечного источника S до т. М прямолинейно. В связи с этим свет при распространении можно рассматривать в виде лучей.

Метод векторных диаграмм

Рис. 8.3

Амплитуды и фазы световых волн (колебаний) в задачах на дифракцию с использованием зон Френеля можно найти графически. Все зоны разбивают еще на ряд равных по амплитуде участков. Каждый из них отличается от соседнего участка по фазе на величину Dj = p/N, где N - число частей, на которые разбита одна зона. Колебания на краю зон отличаются по фазе на p. Результирующая амплитуда волны каждой зоны 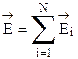,где E_i - амплитуда i-го участка зоны. Колебание, возбуждаемое каждым участком первой зоны, будем характеризовать вектором 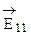, который направлен под углом Dj₁₁ = p / N, например, к оси Х (рис. 8.3). Колебания второго участка изобразим таким же вектором, но направленным под углом Dj₂₁ к первому вектору и т. д. В результате построения всей векторной диаграммы для одной зоны вектор, представляющий колебание последнего участка зоны, своим концом замкнет многоугольник в т. А. (на рис. 8.3 зона состоит из N = 8 участков). Следовательно, вектор = - амплитуда результирующего колебания всей первой зоны I, а результирующая фаза j₁ = p/2. На рис. 8.3 вектором 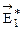= изображена амплитуда колебания,

возбуждаемой от открытой половины первой зоны. Ее фаза Dj = p/4. При распространении неограниченной волны вся бесконечная совокупность

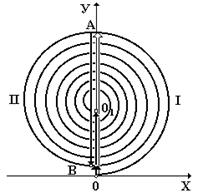Рис. 8.4

зон дает векторную диаграмму, в пределе переходящую в спираль (рис. 6.4). Амплитуда результирующего колебания = = 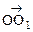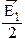, а ее фаза j = p/2. Например, при открытых двух зонах, вектор 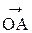даст амплитуду волны первой зоны I, а вектор 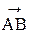- второй зоны II). Эти векторы направлены противоположно, поэтому их результирующая амплитуда равна вектору 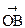(рис. 8.4). Метод векторных диаграмм для нахождения амплитуд и фаз удобен при решении задач, когда имеет место перекрытие непрозрачным экраном ряда или части зон. Метод расчета освещенности за системой экранов с использованием зон Френеля положен в основу теории зонных пластинок.

Действительно, интенсивность максимумов дифракционной картины в т. М можно увеличить, если использовать амплитудную зонную пластинку, в которой, например, все четные зоны (пластинка со светлым центром) или все нечетные (пластинка с темным центром) можно перекрыть непрозрачным экраном. Тогда при А₁ = А₃ = А₅ = ... А_рез= А₁ + А₃ +А₅+ ...= N 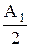. (8.11)

Интенсивность J = 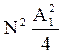. (8.13)

Еще больший эффект можно получить с помощью фазовой зонной пластинки (Релей, Вуд), в которой, регулируя толщины пластинки, можно фазу колебания, например, четных зон Френеля или нечетных, изменить на, противоположную.

Тогда А = 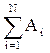=2N 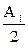. (8.14)

Соответственно интенсивность J = 4N²A₁²/4. (8.15)

Метод зон Френеля качественно объясняет причину появления светлого пятна в центре тени от круглого диска (пятно Пуассона), которое создано вторичными волнами от первой кольцевой зоны Френеля, окружающей диск.