Последовательность работы машины Тьюринга
1) Чтение входной переменной
2) Замещение ее выходной переменной
3) Перемещение в соответствии с управлением
4) Установка следующего состояния
Например: дана машина Тьюринга, которая должна осуществлять организацию алгоритма сложения 2-х чисел (целых и представленных в виде последовательности единиц).
| 4 – 1111 | 1111+111111 |
| 6 – 111111 |
Пустой символ – Λ
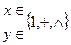 - входной алфавит.
- входной алфавит.
Алгоритм управления {П, Л, Н};
Алгоритм состояний {S1, S2, S3}
| S(ν) x(ν) | S1 | S2 | S3 |
| ЛПS3 | 1ЛS2 | 1ПS3 | |
| Λ | ЛПS1 | ЛПS1 | 1НS2 |
| + | ЛН! | +ЛS2 | +ПS3 |
! – стоп-состояние, останов алгоритма.
Исходное состояние S1
| S1 | S3 | S3 | S3 | S3 | S3 | S3 | S3 | S3 | S3 |
| + |
I такт
1)вместо 1 запишется Λ;
2)перемещение вправо;
3)переход в S3.
II такт
1) записываем 1;
2)перемещение вправо;
3)переход в S3.
……..
V такт
1) записываем +;
2)перемещение вправо;
3)переход в S3.
…..
XII такт
На входе пустое поле (Λ)
1) записываем 1;
2)не перемещаемся;
3)переход в S2.
XIII такт
На входе 1
1) записываем 1;
2) перемещение влево;
3)переход в S2.
……
(N-1) такт
Пустой на входе
1) записываем Λ;
2) перемещение вправо;
3)переход в S1.
N такт
На входе +
1) записываем Λ;
2) не перемещаемся;
3)останов алгоритма.
Начальное входное слово 1111+111111, конечное выходное слово 1111111111.
Машина Тьюринга может реализовывать бесконечное множество различных алгоритмов. Но некоторые задачи не могут быть решены с помощью машины Тьюринга.
Машина Тьюринга представляет собой простейшую систему для реализации алгоритмов.
Алгоритм в ней реализуется на наиболее низком уровне, поэтому более сложные подходы к реализации алгоритмов содержат внутри себя подалгоритмы, реализуемые с помощью машины Тьюринга.
Это позволило сформулировать тезис Тьюринга: функция вычислена с помощью какого-нибудь алгоритма тогда и только тогда, когда она вычислима с помощью машины Тьюринга.
Рассмотрим в качестве примера машину Тьюринга, алгоритм работы которой задан следующей функциональной схемой.
| S0 | S1 | S2 | S3 | |
| аПS2 | 1ЛS1 | 1ПS2 | 1HS3 | |
| Λ | ΛПS0 | ΛПS0 | 1HS1 | ΛПS0 |
| * | *HS3 | *ЛS1 | *ПS2 | ΛHS3 |
| а | аПS0 | аПS0 | 1HS1 | 1ЛS3 |
Необходимо смоделировать работу данной машины и выявить реализуемую ей математическую зависимость.
Исходное состояние S0, символ 11*111
1. S0 11*111 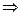 П,S2;
П,S2;
⌂
2. S2 а1*111 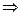 П,S2;
П,S2;
⌂
3. S2 а1*111 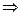 П,S2;
П,S2;
⌂
4. S2 а1*111 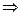 П,S2;
П,S2;
⌂
5. S2 а1*111 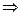 П,S2;
П,S2;
⌂
6. S2 а1*111 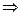 П,S2;
П,S2;
⌂
7. S2 а1*111^ 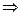 H,S1;
H,S1;
⌂
8. S1 а1*1111 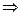 Л,S1;
Л,S1;
⌂
9. S1 а1*1111 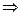 Л,S1;
Л,S1;
⌂
10. S1 а1*1111 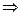 Л,S1;
Л,S1;
⌂
11. S1 а1*1111 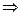 Л,S1;
Л,S1;
⌂
12. S1 а1*1111 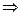 Л,S1;
Л,S1;
……… ⌂
14. S1 а1*1111 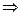 П,S0;
П,S0;
⌂
15. S0 а1*1111 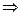 П,S2;
П,S2;
⌂
16. S2 аа*1111 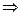 П,S2;
П,S2;
…………
S1 аа*11111  Л,S1;
Л,S1;
………………..ааа111111
Это алгоритм умножения.
Для некоторых алгоритмов процесс их выполнения зависит от исходных данных. При некоторых исходных данных цикл работы можно считать бесконечным.
Дата добавления: 2016-02-02; просмотров: 2099;
