Глава V. Теория атома водорода и водородоподобных атомов.
§ 5.1. Стационарные состояния.
 Стационарными называют состояния, энергия системы в которых не зависит от времени. Таким образом, чтобы найти энергии в этих состояниях, необходимо решить стационарное уравнение Шредингера. Рассмотрим потенциальную энергию частицы:
Стационарными называют состояния, энергия системы в которых не зависит от времени. Таким образом, чтобы найти энергии в этих состояниях, необходимо решить стационарное уравнение Шредингера. Рассмотрим потенциальную энергию частицы: 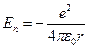 . Решим уравнение Шредингера для потенциальной составляющей:
. Решим уравнение Шредингера для потенциальной составляющей: 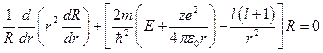 . Введём следующие обозначения:
. Введём следующие обозначения: 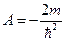 ;
; 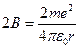 . Осуществим замену переменных:
. Осуществим замену переменных: 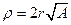 ,
, 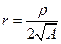 ;
; 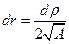 . Тогда, после подстановки новых переменных наше уравнение примет вид:
. Тогда, после подстановки новых переменных наше уравнение примет вид: 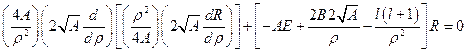 . Упростим данное выражение:
. Упростим данное выражение: 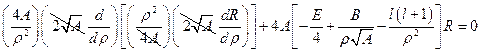 . Произведём дифференцирование:
. Произведём дифференцирование: 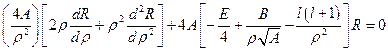 . Раскроем скобки и запишем в виде обыкновенного дифференциального уравнения:
. Раскроем скобки и запишем в виде обыкновенного дифференциального уравнения: 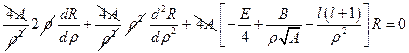 ,
, 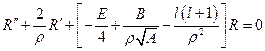 (1). Решение данного уравнения будем искать по тому же алгоритму, что и для гармонического осциллятора.
(1). Решение данного уравнения будем искать по тому же алгоритму, что и для гармонического осциллятора.
1. Рассмотрим сначала асимптотическое решение при 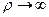 . Тогда уравнение (1) преобразуется к виду:
. Тогда уравнение (1) преобразуется к виду: 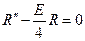 . Решением его, очевидно, будет функция
. Решением его, очевидно, будет функция 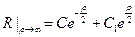 . Чтобы решение было ограничено на бесконечности, необходимо положить
. Чтобы решение было ограничено на бесконечности, необходимо положить 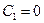 . Таким образом,
. Таким образом, 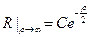 .
.
2. Теперь рассмотрим ассимптотику при 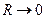 . Принебрегая членами со степенями
. Принебрегая членами со степенями 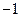 , получим из уравнения Шредингера:
, получим из уравнения Шредингера: 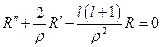 . Решение данного уравнения будем искать в виде:
. Решение данного уравнения будем искать в виде: 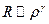 . Подставляем предпологаемое решение в преобразованное уравнение Шредингера. Получим:
. Подставляем предпологаемое решение в преобразованное уравнение Шредингера. Получим: 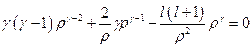 ,
, 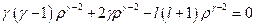 ,
, 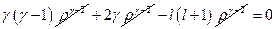 ;
; 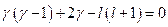 . Мы получили уравнение относительно
. Мы получили уравнение относительно 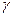 . Раскроем скобки, приведём его к стандартному виду и найдём решение.
. Раскроем скобки, приведём его к стандартному виду и найдём решение. 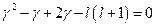 ,
, 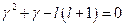 . Решением этого алгебраического уравнения будет
. Решением этого алгебраического уравнения будет 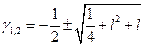 . Или, так как
. Или, так как 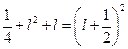 ,
, 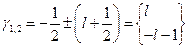 . Если
. Если 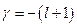 , то
, то 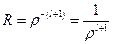 . При
. При 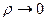 ,
, 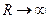 . Поэтому данное значение
. Поэтому данное значение 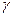 придётся отбросить. Таким образом, остаётся решение такого вида:
придётся отбросить. Таким образом, остаётся решение такого вида: 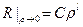 .
.
Итак, у нас есть решения при асимптотическом стремлении 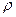 к нулю и к бесконечности. Тогда решение для радиальной составляющей волновой функции мы будем искать в виде произведения:
к нулю и к бесконечности. Тогда решение для радиальной составляющей волновой функции мы будем искать в виде произведения: 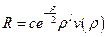 . Здесь
. Здесь 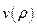 – некоторая функция, которая определяет поведение
– некоторая функция, которая определяет поведение 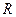 в промежутке от нуля до бесконечности. Подставляем данный вид решения в уравнение (1). После взятия производных и упрощения, получим:
в промежутке от нуля до бесконечности. Подставляем данный вид решения в уравнение (1). После взятия производных и упрощения, получим: 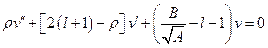 (2). Введём ограничения на функцию
(2). Введём ограничения на функцию 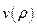 : она не должна на бесконечности расти быстрее, чем
: она не должна на бесконечности расти быстрее, чем 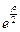 , а в нуле должна либо обращаться в ноль, либо быть константой. Эти обстоятельства наводит на мысль, что функцию
, а в нуле должна либо обращаться в ноль, либо быть константой. Эти обстоятельства наводит на мысль, что функцию 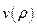 следует искать в виде полинома:
следует искать в виде полинома: 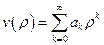 . Подставим этот предполагаемый вид решения в уравнение (2). Вычислим первую и вторую производные:
. Подставим этот предполагаемый вид решения в уравнение (2). Вычислим первую и вторую производные: 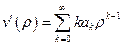 ,
, 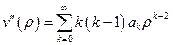 . Тогда:
. Тогда:
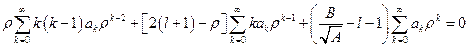
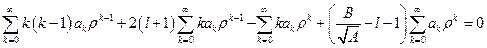
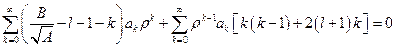 .
.
Данный многочлен будет равен нулю только в том случае, когда коэффициенты при каждой степени 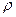 будут равны нулю. Запишем это условие:
будут равны нулю. Запишем это условие: 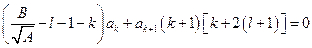 . Данное соотношение даёт рекуррентную формулу для коэффициентов
. Данное соотношение даёт рекуррентную формулу для коэффициентов 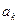 :
: 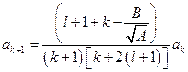 . Оценим коэффициенты
. Оценим коэффициенты 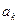 при
при 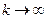 :
: 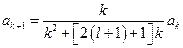 ,
, 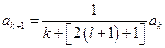 ;
; 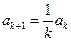 . Таким образом,
. Таким образом, 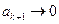 и
и 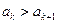 . Тогда при каком-нибудь малом значении
. Тогда при каком-нибудь малом значении 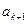 многочлен можно оборвать:
многочлен можно оборвать: 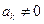 , а
, а 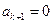 . Данное условие будет выполнено, если коэффициент при
. Данное условие будет выполнено, если коэффициент при 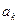 будет равен нулю:
будет равен нулю: 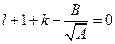 ,
, 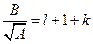 ;
; 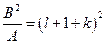 . Вернёмся к обозначениям
. Вернёмся к обозначениям 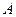 и
и 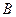 :
: 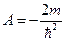 ,
, 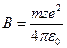 .
. 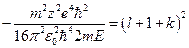 . Сократим:
. Сократим: 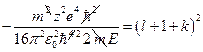 ,
, 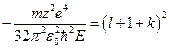 . Из этой формулы следует, что энергия зависит от
. Из этой формулы следует, что энергия зависит от 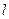 и
и 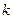 . Введём следующее обозначение:
. Введём следующее обозначение: 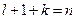 . Тогда
. Тогда 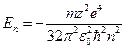 , где
, где 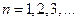 . Таким образом, решая уравнение Шредингера, мы нашли энергии водородоподобного атома, то есть нашли собственные значения оператора Гамильтона. То же самое значение для энергий мы получили, исходя только из постулатов Бора и правила квантования. Схема энергетических уровней будет совпадать со схемой энергетических уровней по Бору. Теория Бора не объясняет, почему главное квантовое число имеет своим первым значением 1. Квантовая же теория показывает, что при
. Таким образом, решая уравнение Шредингера, мы нашли энергии водородоподобного атома, то есть нашли собственные значения оператора Гамильтона. То же самое значение для энергий мы получили, исходя только из постулатов Бора и правила квантования. Схема энергетических уровней будет совпадать со схемой энергетических уровней по Бору. Теория Бора не объясняет, почему главное квантовое число имеет своим первым значением 1. Квантовая же теория показывает, что при 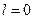 и
и 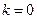 минимально возможное значение главного квантового числа будет 1. Напомним, как называются числа
минимально возможное значение главного квантового числа будет 1. Напомним, как называются числа 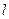 ,
, 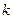 и
и 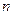 .
. 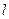 – орбитальное квантовое число,
– орбитальное квантовое число, 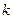 – радиальное квантовое число и
– радиальное квантовое число и 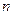 – главное квантовое число.
– главное квантовое число.
Теория Бора исходила из тех принципов, что электроны движутся в атоме по круговым орбитам по законам классической механики, но в противоречие классической электродинамике ускоренно движущиеся электроны не излучают. В квантовой теории интерпретация движения электронов иная. Вообще нельзя говорить о движении электронов по какой-либо траектории, то есть нельзя представить координаты электрона как функцию времени. Поэтому используется представление о состоянии движения электрона, описываемом той или иной волновой функцией. Причём состояние движения электрона не всегда имеет классический аналог. Например, рассмотрим состояние электрона, при котором 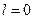 . Это значит, в силу правила квантования:
. Это значит, в силу правила квантования: 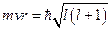 , что так как скорость движения электрона отлична от нуля,
, что так как скорость движения электрона отлична от нуля, 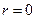 , то есть плечо не имеет длины. Это возможно в том случае, если электрон движется вдоль радиуса, то есть проходит на пути своего движения сквозь ядро.
, то есть плечо не имеет длины. Это возможно в том случае, если электрон движется вдоль радиуса, то есть проходит на пути своего движения сквозь ядро.
§ 5.2. Атомы щелочных металлов.
Для атома водорода нахождение уровней энергий является несложной аналитической задачей. Если в атоме существуют несколько электронов, то решение уравнения Шредингера существенно усложняется. В настоящее время ни точного аналитического, ни точного численного решения ещё не получено. Существуют лишь приближённые решения.
Щелочные металлы в таблице Менделеева следуют за благородными газами, то есть их атомы содержат на один электрон больше, чем атомы инертных газов. Поэтому эти металлы легко ионизировать. Энергетическое строение атомов щелочных металлов близко к строению атома водорода. Если атом щелочного металла имеет 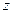 электронов, то
электронов, то 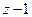 электрон образуют структуру, схожую с атомом инертного газа, называемую атомным остовом. Связь последнего электрона с остовом слабая, поэтому можно считать, что валентный электрон движется в эффективном поле атомного остова. Однако валентный электрон деформирует оболочку и искажает потенциальное поле кулоновских сил, в котором сам же и двигается. Поэтому потенциальная энергия валентного электрона моет быть представлена в виде:
электрон образуют структуру, схожую с атомом инертного газа, называемую атомным остовом. Связь последнего электрона с остовом слабая, поэтому можно считать, что валентный электрон движется в эффективном поле атомного остова. Однако валентный электрон деформирует оболочку и искажает потенциальное поле кулоновских сил, в котором сам же и двигается. Поэтому потенциальная энергия валентного электрона моет быть представлена в виде: 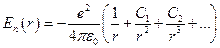 . Здесь слагаемые со степенью
. Здесь слагаемые со степенью 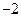 и выше образуют поправку на влияние на искажение поля электроном. Ограничимся поправкой пропорциональной
и выше образуют поправку на влияние на искажение поля электроном. Ограничимся поправкой пропорциональной 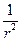 . Тогда уравнение Шредингера для радиальной части волновой функции примет вид:
. Тогда уравнение Шредингера для радиальной части волновой функции примет вид: 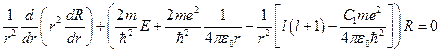 . Данное уравнение будет полностью совпадать с уравнением Шредингера, которое мы уже решили, если положить
. Данное уравнение будет полностью совпадать с уравнением Шредингера, которое мы уже решили, если положить 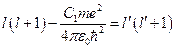 . Раскрыв скобки и решив полученное квадратное уравнение относительно
. Раскрыв скобки и решив полученное квадратное уравнение относительно 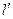 , получим:
, получим: 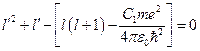 ;
; 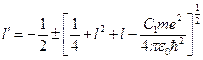 . Здесь
. Здесь 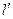 должно быть больше нуля, иначе угловая часть волновой функции будет бесконечна. Тогда
должно быть больше нуля, иначе угловая часть волновой функции будет бесконечна. Тогда 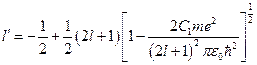 . Так как электрон не очень сильно искажает кулоновское поле, то в подкоренном выражении можно разложить в ряд второе слагаемое, так как оно гораздо меньше единицы. Ограничимся только первым слагаемым:
. Так как электрон не очень сильно искажает кулоновское поле, то в подкоренном выражении можно разложить в ряд второе слагаемое, так как оно гораздо меньше единицы. Ограничимся только первым слагаемым: 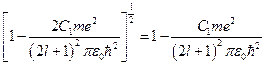 . Тогда
. Тогда 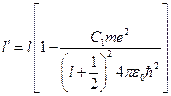 . Размерность
. Размерность 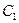 – метр.
– метр. 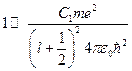 , но
, но 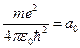 – радиус первой боровской орбиты. Тогда
– радиус первой боровской орбиты. Тогда 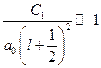 . Здесь
. Здесь 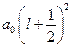 – среднее расстояние от ядра до ближайшего электрона имеет порядок
– среднее расстояние от ядра до ближайшего электрона имеет порядок 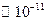 м. Таким образом, поправка действительно мала. Тогда для атома щелочного металла главное квантовое число будет:
м. Таким образом, поправка действительно мала. Тогда для атома щелочного металла главное квантовое число будет: 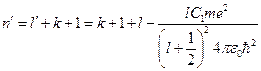 . Введём обозначение:
. Введём обозначение: 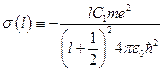 . Следовательно,
. Следовательно, 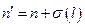 . Тогда выражение для уровней энергии щелочного металла примет вид:
. Тогда выражение для уровней энергии щелочного металла примет вид: 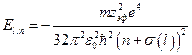 , где
, где 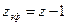 , а
, а 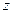 – заряд ядра.
– заряд ядра.
 Рассмотрим энергетическую структуру
Рассмотрим энергетическую структуру 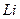 . Литий – щелочной металл. В таблице Менделеева он идёт сразу за инертным газом гелием, поэтому имеет соответственно на один электрон больше, чем
. Литий – щелочной металл. В таблице Менделеева он идёт сразу за инертным газом гелием, поэтому имеет соответственно на один электрон больше, чем 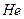 . Литий обладает тремя электронами, два из которых образуют вместе с ядром устойчивую структуру, – атомный остов, а на внешнем энергетическом уровне расположен лишь один валентный электрон. Главное квантовое число лития в основном состоянии равно двум:
. Литий обладает тремя электронами, два из которых образуют вместе с ядром устойчивую структуру, – атомный остов, а на внешнем энергетическом уровне расположен лишь один валентный электрон. Главное квантовое число лития в основном состоянии равно двум: 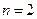 ; основное состояние –
; основное состояние – 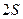 . Рассмотрим главное квантовое число:
. Рассмотрим главное квантовое число: 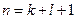 . Тогда, если
. Тогда, если 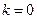 , то
, то 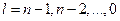 .Тогда
.Тогда 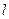 в состоянии
в состоянии 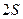 равно 0, но из последней формулы следует, что
равно 0, но из последней формулы следует, что 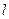 может быть также равно 1. Это даёт состояние
может быть также равно 1. Это даёт состояние 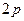 . Энергия в этом состоянии больше, чем для случая
. Энергия в этом состоянии больше, чем для случая 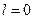 , так как
, так как 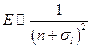 ,
, 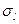 здесь меньше нуля. Очевидно, что для
здесь меньше нуля. Очевидно, что для 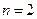
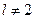 , поэтому состояние
, поэтому состояние 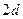 невозможно. Невозможны также состояния
невозможно. Невозможны также состояния 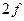 и
и 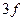 . Переходы между различными состояниями осуществляются по правилам отбора: в атоме возможны только те оптические переходы, в которых дипольный момент перехода не равен нулю. Под дипольным моментом
. Переходы между различными состояниями осуществляются по правилам отбора: в атоме возможны только те оптические переходы, в которых дипольный момент перехода не равен нулю. Под дипольным моментом 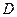 понимают переход между квантовыми уровнями с числами
понимают переход между квантовыми уровнями с числами 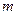 и
и 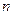 :
: 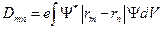 , где
, где 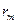 ,
, 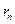 –
–
Правило отбора: 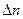 принимает любое значение, а
принимает любое значение, а 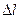 – только
– только 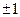 . В соответствии с данным правилом, для лития существует переход из
. В соответствии с данным правилом, для лития существует переход из 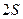 в
в 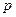 состояния. Такой переход называют главным, а спектральные линии, полученные при таком переходе – главной серией:
состояния. Такой переход называют главным, а спектральные линии, полученные при таком переходе – главной серией: 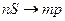 . Для лития:
. Для лития: 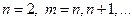 . Не запрещённые правилами отбора переходы
. Не запрещённые правилами отбора переходы 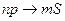 ,
, 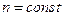 дают группу спектральных линий, соответствующую этим переходам, которую называют резкой серией. Не запрещены также переходы
дают группу спектральных линий, соответствующую этим переходам, которую называют резкой серией. Не запрещены также переходы 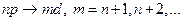 . Для лития
. Для лития 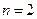 ; для натрия
; для натрия 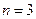 . Данные переходы образуют диффузную серию.
. Данные переходы образуют диффузную серию.
Спектральным разрешением спектрального прибора называют величину 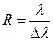 , где
, где 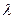 – средняя наблюдаемая длина волны, а
– средняя наблюдаемая длина волны, а 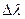 – интервал наблюдаемых волн. Исторически первыми появились приборы с низким
– интервал наблюдаемых волн. Исторически первыми появились приборы с низким 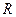 . Поэтому спектр щелочных металлов представлялся набором синглетов. С усовершенствованием спектральной техники, было обнаружено, что каждая «синглетная» линия расщепляется, в свою очередь, на дублет. Причём это расщепление имело следующие закономерности: у линий главной серии расстояние между линиями дублета не являются постоянными, а изменяются от дублета к дублету. У линий диффузной серии расстояние между «расщеплёнными» линиями оставалось одинаковым для всех дублетов; все линии наблюдались нечётко. У линий резкой серии расщепление оставалось постоянным, и линии были видны чётко. Данные факты были объяснены следующим образом.
. Поэтому спектр щелочных металлов представлялся набором синглетов. С усовершенствованием спектральной техники, было обнаружено, что каждая «синглетная» линия расщепляется, в свою очередь, на дублет. Причём это расщепление имело следующие закономерности: у линий главной серии расстояние между линиями дублета не являются постоянными, а изменяются от дублета к дублету. У линий диффузной серии расстояние между «расщеплёнными» линиями оставалось одинаковым для всех дублетов; все линии наблюдались нечётко. У линий резкой серии расщепление оставалось постоянным, и линии были видны чётко. Данные факты были объяснены следующим образом.
Было выдвинуто предположение, что энергия состояния должна зависеть ещё от какого-либо квантового числа и это изменение энергии уровней должно быть маленьким. Поэтому предположили, что электрон в атоме имеет ещё одну дополнительную степень свободы, и если обозначить квантовое число, соответствующее этой дополнительной степени свободы 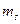 , то энергия уровня должна зависеть от квантовых чисел
, то энергия уровня должна зависеть от квантовых чисел 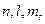 . Таким образом, приписывают электрону внутреннюю степень свободы. Она является собственным механическим моментом импульса; называется спином. Этот момент импульса должен квантоваться. Так как
. Таким образом, приписывают электрону внутреннюю степень свободы. Она является собственным механическим моментом импульса; называется спином. Этот момент импульса должен квантоваться. Так как 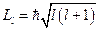 , то, по аналогии,
, то, по аналогии, 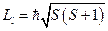 , где
, где 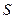 – спиновое квантовое число. Оно может принимать значения:
– спиновое квантовое число. Оно может принимать значения: 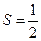 . Запишем проекцию момента импульса на различные направления:
. Запишем проекцию момента импульса на различные направления: 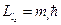 . Тогда по аналогии
. Тогда по аналогии 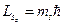 , где
, где 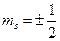 . Для объяснения экспериментальных фактов наряду со спином допускается наличие у электрона магнитного момента, который связывают со спином соотношением:
. Для объяснения экспериментальных фактов наряду со спином допускается наличие у электрона магнитного момента, который связывают со спином соотношением: 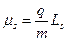 , где
, где 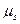 – магнитный момент электрона. Относительно некоторого произвольного направления магнитный момент может быть ориентирован двумя способами:
– магнитный момент электрона. Относительно некоторого произвольного направления магнитный момент может быть ориентирован двумя способами: 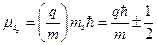 , то есть существуют только два значения магнитного момента. Это как раз и объясняет дублетный характер спектров щелочных металлов, так как наличие магнита приводит к дополнительному взаимодействию в атоме, называемому спин-орбитальным взаимодействием. Оно обусловлено взаимодействием магнитных моментов во внешнем магнитном поле:
, то есть существуют только два значения магнитного момента. Это как раз и объясняет дублетный характер спектров щелочных металлов, так как наличие магнита приводит к дополнительному взаимодействию в атоме, называемому спин-орбитальным взаимодействием. Оно обусловлено взаимодействием магнитных моментов во внешнем магнитном поле: 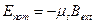 . Существует три различных объяснения процесса данного взаимодействия:
. Существует три различных объяснения процесса данного взаимодействия:
1. Электрон при движении вокруг ядра создаёт круговой ток. Этот ток порождает магнитное поле, которое взаимодействует с магнитным же полем электрона. Данное объяснение обладает внутри себя некоторой неувязкой. Дело в том, что нельзя определить магнитное поле внутри электрона.
2. Движущийся магнитный момент обладает дипольным моментом: 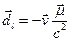 . Энергия взаимодействия этого дипольного момента с кулоновским полем ядра равна
. Энергия взаимодействия этого дипольного момента с кулоновским полем ядра равна 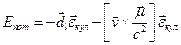 .
.
3. Перейдём в систему координат, связанную с электроном, движущимся вокруг ядра. В этой системе координат электрон покоится, а ядро движется вокруг электрона. При своём движении положительно заряженное ядро создаёт в точке нахождения электрона магнитное поле, которое приводит к дополнительному энергетическому взаимодействию: 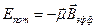 .
.
Эта энергия называется энергией спин-орбитального взаимодействия и зависит от проекций 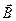 и
и 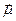 . Пусть орт
. Пусть орт 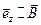 . Тогда потенциальная энергия может принимать два значения:
. Тогда потенциальная энергия может принимать два значения: 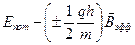 . Таким образом,
. Таким образом, 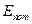 можно либо прибавить, либо отнять, то есть получается два уровня энергии.
можно либо прибавить, либо отнять, то есть получается два уровня энергии.
Расщепление уровня энергии, вызванное спин-орбитальным взаимодействием называется тонким
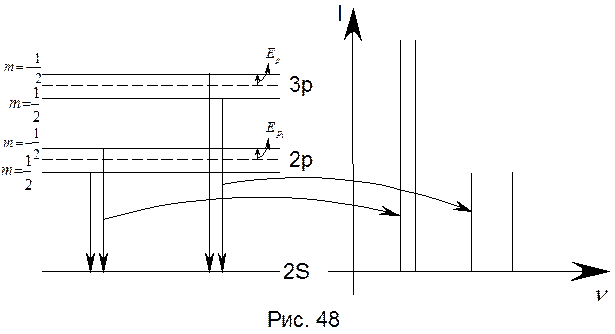
расщеплением, а структура спектральных линий, соответствующая переходам между расщеплёнными уровнями, называется тонкой структурой. Но не все энергетические уровни имеют тонкую структуру. Например, энергетические уровни 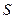 не имеют тонкой структуры. Их называют синглетными. Тонкая структура полностью объясняет спектр щелочного металла: все уровни, исключая
не имеют тонкой структуры. Их называют синглетными. Тонкая структура полностью объясняет спектр щелочного металла: все уровни, исключая 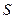 , дублетны, а
, дублетны, а 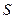 – синглетны.
– синглетны.
Энергия спин-орбитального взаимодействия очень мала, поэтому при оптических переходах ориентировка спина не меняется. В связи с этим применяется правило отбора: 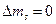 .
.
Рассмотрим теперь в связи с выше полученными данными структуру энергетических уровней атома лития.
1. Главная серия: 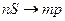 .
.
Здесь 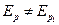 , так как зависят они от главного квантового числа. Поэтому для различных главных квантовых чисел расстояние между дублетными линиями будет различно. Распределение интенсивности излучения в зависимости от частоты носит характер, представленный на рисунке 48. Интенсивность зависит от числа перехода переходов с данного энергетического уровня. Очевидно, что наибольшее число переходов осуществляется между близлежащими уровнями.
, так как зависят они от главного квантового числа. Поэтому для различных главных квантовых чисел расстояние между дублетными линиями будет различно. Распределение интенсивности излучения в зависимости от частоты носит характер, представленный на рисунке 48. Интенсивность зависит от числа перехода переходов с данного энергетического уровня. Очевидно, что наибольшее число переходов осуществляется между близлежащими уровнями.
2. Резкая серия. 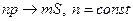 .
.
Расстояние между компонентам дублета постоянно, так как для каждой линии оно обусловлено расщеплением только одного уровня 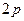 .
.
3. Диффузная серия. 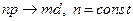 .
.
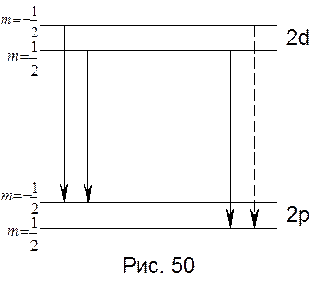
 Расщепление уровней
Расщепление уровней 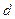 много меньше, чем расщепление уровня
много меньше, чем расщепление уровня 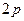 . Фактически при переходах с уровней
. Фактически при переходах с уровней 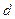 на уровень
на уровень 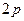 получаются три линии, поскольку изображённый штриховой линией (см. рис. 50) переход запрещён правилами отбора. Однако две линии, получающиеся при переходе с двух расщеплённых уровней
получаются три линии, поскольку изображённый штриховой линией (см. рис. 50) переход запрещён правилами отбора. Однако две линии, получающиеся при переходе с двух расщеплённых уровней 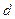 на один и тот же уровень
на один и тот же уровень 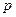 , расположены весьма близко друг к другу и практически сливаются. Благодаря этому они воспринимаются как размытая линия. Расщепление же между парой линий и одиночной линией весьма значительно. Поэтому в целом все эти три линии воспринимаются как дублет из размытых линий. Расщепление дублета у всех линий серии одно и то же, поскольку оно определяется расщеплением одного и того же уровня
, расположены весьма близко друг к другу и практически сливаются. Благодаря этому они воспринимаются как размытая линия. Расщепление же между парой линий и одиночной линией весьма значительно. Поэтому в целом все эти три линии воспринимаются как дублет из размытых линий. Расщепление дублета у всех линий серии одно и то же, поскольку оно определяется расщеплением одного и того же уровня 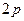 .
.
§ 5.3. Магнитный и механический момент электрона.
Движение электрона вокруг ядра эквивалентно круговому току. Магнитный момент тока определяется по известной формуле: 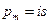 , где
, где 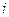 – ток, протекающий по контуру, а
– ток, протекающий по контуру, а 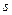 – площадь контура. В случае электрона
– площадь контура. В случае электрона 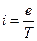 , где
, где  – заряд электрона, а
– заряд электрона, а 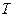 – период его обращения вокруг ядра. Таким образом,
– период его обращения вокруг ядра. Таким образом, 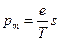 , здесь
, здесь 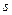 – площадь, охватываемая орбитой электрона. Как уже было сказано выше, электрон движется в поле центральных сил. В поле центральных сил момент импульса является интегралом движения1. Поэтому в полярной системе координат:
– площадь, охватываемая орбитой электрона. Как уже было сказано выше, электрон движется в поле центральных сил. В поле центральных сил момент импульса является интегралом движения1. Поэтому в полярной системе координат: 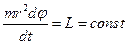 . Пусть начало координат совпадает с ядром. Площадь орбиты электрона есть:
. Пусть начало координат совпадает с ядром. Площадь орбиты электрона есть: 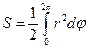 . Из предыдущей формулы найдём
. Из предыдущей формулы найдём 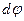 :
: 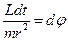 . Тогда:
. Тогда: 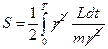 ;
; 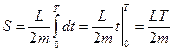 . Тогда магнитный момент электрона:
. Тогда магнитный момент электрона: 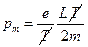 ,
, 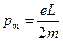 . Для положительно заряженной частицы вектора
. Для положительно заряженной частицы вектора 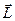 и
и 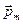 коллинеарны. В общем же случае:
коллинеарны. В общем же случае: 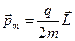 . Применительно же к электрону,
. Применительно же к электрону, 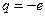 ,
, 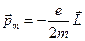 . Таким образом, мы получили связь между магнитным и механическим моментом электрона. Совершим некоторые преобразования. Умножим последнюю формулу на дробь
. Таким образом, мы получили связь между магнитным и механическим моментом электрона. Совершим некоторые преобразования. Умножим последнюю формулу на дробь 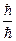 . Получим:
. Получим: 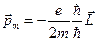 . Введём следующее обозначение:
. Введём следующее обозначение: 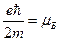 . Величину
. Величину 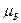 называют магнетоном Бора. Тогда последняя формула перепишется так:
называют магнетоном Бора. Тогда последняя формула перепишется так: 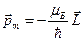 . В системе СИ
. В системе СИ 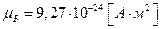 . По аналогии квантово-механический магнитный момент связан с квантово-механическим орбитальным моментом таким же соотношением:
. По аналогии квантово-механический магнитный момент связан с квантово-механическим орбитальным моментом таким же соотношением: 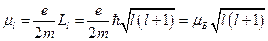 . Найдём выражение для проекции магнитного
. Найдём выражение для проекции магнитного
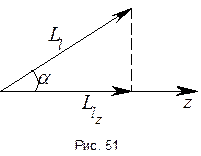
момента на какую-либо ось, например, на ось 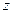 :
: 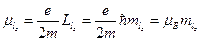 , где
, где 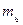 – проекция орбитального момента на заданное направление. Так как
– проекция орбитального момента на заданное направление. Так как 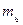 может принимать только
может принимать только 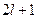 значение:
значение: 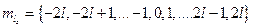 , то существует
, то существует 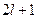 способа ориентации магнитного момента. Так как в сферически симметричной системе координат в качестве оси
способа ориентации магнитного момента. Так как в сферически симметричной системе координат в качестве оси 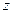 можно выбрать любую, то и полученное соотношение будет справедливо для проекции магнитного момента на любую ось.
можно выбрать любую, то и полученное соотношение будет справедливо для проекции магнитного момента на любую ось.
Рассмотрим углы, которые образует орбитальный момент с осью 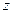 .
. 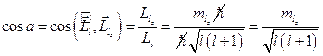 . Максимальное значение, которое может принимать орбитальное квантовое число –
. Максимальное значение, которое может принимать орбитальное квантовое число – 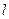 , поэтому
, поэтому 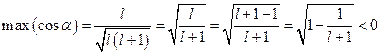 , так как
, так как 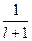 – величина положительная. Таким образом, квантово-механический орбитальный момент никогда не может быть сонаправленым с осью, относительно которой он рассматривается. Вообще говоря, он не может быть ориентирован строго по какой-либо определённой оси. Причём
– величина положительная. Таким образом, квантово-механический орбитальный момент никогда не может быть сонаправленым с осью, относительно которой он рассматривается. Вообще говоря, он не может быть ориентирован строго по какой-либо определённой оси. Причём 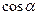 может принимать только различные дискретные значения, в зависимости от
может принимать только различные дискретные значения, в зависимости от 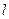 . Эта дискретность в ориентации момента импульса называется пространственным квантованием.
. Эта дискретность в ориентации момента импульса называется пространственным квантованием.
Отношение 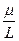 модуля магнитного момента к модулю механического момента, выраженное в единицах
модуля магнитного момента к модулю механического момента, выраженное в единицах 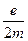 , называется гиромагнитным отношением:
, называется гиромагнитным отношением: 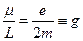 . Очевидно, что для орбитального и магнитного и механического моментов электрона гиромагнитное соотношение равно единице, т. е.
. Очевидно, что для орбитального и магнитного и механического моментов электрона гиромагнитное соотношение равно единице, т. е. 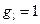 . Для собственного магнитного момента электрона, обусловленного наличием спина:
. Для собственного магнитного момента электрона, обусловленного наличием спина: 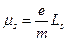 . Тогда гиромагнитное отношение для спинового магнитного момента и механического момента
. Тогда гиромагнитное отношение для спинового магнитного момента и механического момента 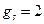 .
.
Итак, электрон обладает в атоме четырьмя моментами:
1. Механическим (орбитальным и спиновым);
2. Магнитным (орбитальным и спиновым).
Полный механический момент импульса электрона является векторной суммой орбитального механического момента и спинового механического момента: 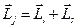 . Так как модули каждого момента всегда квантуются:
. Так как модули каждого момента всегда квантуются: 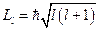 ,
, 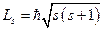 то и их сумма должна квантоваться:
то и их сумма должна квантоваться: 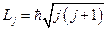 , где
, где 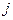 – квантовое число полного механического момента электрона. Найдём его. Рассмотрим значения проекций на ось
– квантовое число полного механического момента электрона. Найдём его. Рассмотрим значения проекций на ось 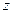 :
: 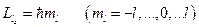 –
– 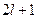 значение;
значение; 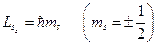 . Тогда
. Тогда 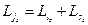 ;
; 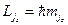 , где
, где 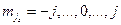 –
– 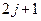 значение. Так как
значение. Так как 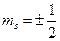 ,
,
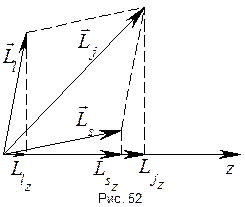
то тогда 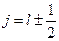 . Определим угол между орбитальным и спиновым моментами электрона. Так как
. Определим угол между орбитальным и спиновым моментами электрона. Так как 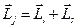 , то, возводя это выражение в квадрат, получим:
, то, возводя это выражение в квадрат, получим: 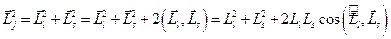 . Отсюда
. Отсюда 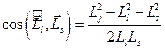 , или
, или 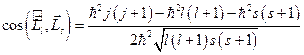 . Так как возможно лишь
. Так как возможно лишь 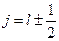 – 2 состояния, то существует 2 возможных угла между орбитальным и спиновым моментами. Так как направление момента относительно любой оси не определено, то возникает вопрос, что же понимать под углом между этими моментами? Смысл данного угла в том, что в отсутствии внешних сил полный момент импульса сохраняется, орбитальный и спиновой моменты прецессируют вокруг полного момента, а их проекции на направление полного момента имеют вполне определённые значения (рис. 53).
– 2 состояния, то существует 2 возможных угла между орбитальным и спиновым моментами. Так как направление момента относительно любой оси не определено, то возникает вопрос, что же понимать под углом между этими моментами? Смысл данного угла в том, что в отсутствии внешних сил полный момент импульса сохраняется, орбитальный и спиновой моменты прецессируют вокруг полного момента, а их проекции на направление полного момента имеют вполне определённые значения (рис. 53).

Полный магнитный момент электрона равен сумме векторов орбитального магнитного момента и спинового магнитного момента: 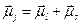 . Так как
. Так как 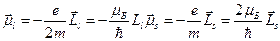 . Таким образом, гиромагнитное отношения для механических и магнитных моментов различны. Поэтому полный механический и полный магнитный момент не коллинеарны.
. Таким образом, гиромагнитное отношения для механических и магнитных моментов различны. Поэтому полный механический и полный магнитный момент не коллинеарны.
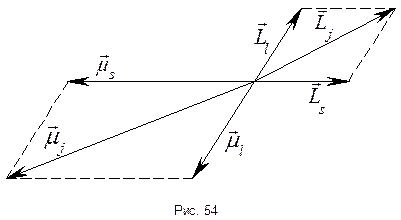
§ 5.4.Векторная модель атома. Правила сложения моментов.
Полный магнитный и механический моменты атома складываются из механических орбитальных и спиновых моментов, и магнитных орбитальных и спиновых моментов всех электронов, образующих оболочку атома. Поведение вектора полного момента атома зависит от способа и последовательности сложения отдельных моментов. Рассмотрим общий метод сложения моментов с учётом пространственного квантования на примере для двух электронов.
Пусть на внешней оболочке атома находятся два электрона. Орбитальный и механический моменты этих электронов будут 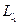 и
и 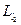 , где
, где 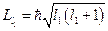 и
и 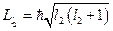 . Суммарный момент для атома равен векторной сумме
. Суммарный момент для атома равен векторной сумме 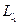 и
и 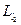 :
: 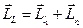 . Очевидно, что он тоже квантуется, так как квантуются моменты его составляющие:
. Очевидно, что он тоже квантуется, так как квантуются моменты его составляющие: 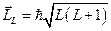 , причём
, причём 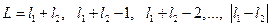 . Число способов, по которым могут складываться два момента равно числу возможных значений квантового числа
. Число способов, по которым могут складываться два момента равно числу возможных значений квантового числа 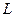 . Найдём их. Пусть сначала
. Найдём их. Пусть сначала 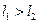 . Тогда
. Тогда 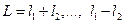 . В этой последовательности чисел до нуля не хватает
. В этой последовательности чисел до нуля не хватает 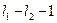 элемента. Тогда количество элементов данной последовательности будет равно:
элемента. Тогда количество элементов данной последовательности будет равно: 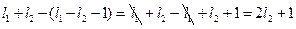 . Аналогично, если
. Аналогично, если 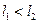 . В этом случае количество элементов данной последовательности будет равно:
. В этом случае количество элементов данной последовательности будет равно: 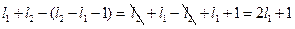 . Таким образом, в общем случае число способов, которыми механические моменты с квантовыми числами
. Таким образом, в общем случае число способов, которыми механические моменты с квантовыми числами 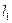 и
и 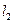 складываются друг с другом, с учётом пространственного квантования, будет
складываются друг с другом, с учётом пространственного квантования, будет 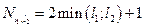 . Проекция полного момента на избранное направление, например ось
. Проекция полного момента на избранное направление, например ось 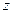 , должно быть равно:
, должно быть равно: 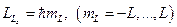 . Таким образом, возможен
. Таким образом, возможен 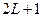 способ ориентации моментов в атоме.
способ ориентации моментов в атоме.
Если в атоме больше двух электронов, то нахождение полного момента осуществляется последовательного применения правил сложения двух моментов. Правило сложения спиновых моментов аналогичны. Каждый их 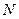 электронов обладает вектором спинового момента
электронов обладает вектором спинового момента 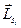 . Тогда общий спиновой момент атома
. Тогда общий спиновой момент атома 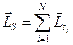 , где
, где 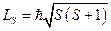 . Квантовое число
. Квантовое число 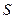 полного спина может принимать значения
полного спина может принимать значения
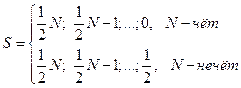
Возможные значения полного момента спина на ось 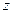 :
: 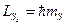 , где
, где 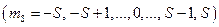 . Таким образом, возможны
. Таким образом, возможны 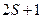 возможности ориентировки спина.
возможности ориентировки спина.
§ 5.5. Типы связи электронов в атоме.
Свойства атома зависят от того, как происходит образование полного механического момента атома. Возможны два способа. Они зависят от того, какие взаимодействия между электронами в атоме преобладают.
1. 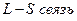 . Реализуется в том случае, если электростатическое взаимодействие между электронами в атоме сильнее, чем спин-орбитальное взаимодействие для каждого электрона. Поэтому сначала находятся полный орбитальный и полный спиновой моменты для каждого электрона, которые потом складываются:
. Реализуется в том случае, если электростатическое взаимодействие между электронами в атоме сильнее, чем спин-орбитальное взаимодействие для каждого электрона. Поэтому сначала находятся полный орбитальный и полный спиновой моменты для каждого электрона, которые потом складываются:
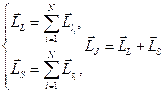 .
.
Полный момент, очевидно1, квантуется: 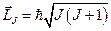 , где
, где 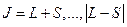 . Как было показано выше, число способов, которыми складываются моменты, равно числу слагаемых:
. Как было показано выше, число способов, которыми складываются моменты, равно числу слагаемых: 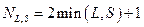 , то есть возможно
, то есть возможно 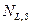 состояний атома. Обычно бывает
состояний атома. Обычно бывает 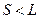 . Тогда
. Тогда 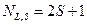 .
. 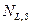 определяет спин-орбитальное расщепление энергетических уровней в атоме и называется мультиплетностью.
определяет спин-орбитальное расщепление энергетических уровней в атоме и называется мультиплетностью.
2. 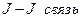 . Этот тип связи реализуется, когда спин-орбитальное взаимодействие в атоме сильнее, чем электростатическое взаимодействие различный электронов друг с другом. Поэтому мы находим сначала полный механический момент всех электронов, а потом – полный момент всего атома как векторную сумму всех полных моментов каждого электрона:
. Этот тип связи реализуется, когда спин-орбитальное взаимодействие в атоме сильнее, чем электростатическое взаимодействие различный электронов друг с другом. Поэтому мы находим сначала полный механический момент всех электронов, а потом – полный момент всего атома как векторную сумму всех полных моментов каждого электрона: 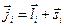 ,
, 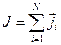 . Этот тип связи реализуется для многоэлектронных атомов (окончание таблицы Менделеева).
. Этот тип связи реализуется для многоэлектронных атомов (окончание таблицы Менделеева).
3. 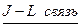 . Моменты части электронов складываются по правилу
. Моменты части электронов складываются по правилу 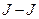 связи, а части – по правилу
связи, а части – по правилу 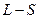 связи. Результирующий момент есть результат векторного сложения этих двух моментов:
связи. Результирующий момент есть результат векторного сложения этих двух моментов: 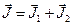 . Эта связь хорошо работает для инертных газов.
. Эта связь хорошо работает для инертных газов.
§ 5.6.Полный магнитный момент атома.
Полный магнитный момент атома складывается из полных спинового и орбитального моментов атома: 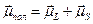 . Для каждого из них мы можем записать:
. Для каждого из них мы можем записать: 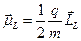 и
и 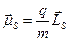 . Таким образом, полный ммагнитный момент не будет лежать на одной оси с полным механическим моментом.
. Таким образом, полный ммагнитный момент не будет лежать на одной оси с полным механическим моментом.
Рассмотри случай изолированного атома. В изолированном атоме 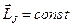 . Если вектор
. Если вектор 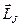 сохраняет своё направление в пространстве, вектора
сохраняет своё направление в пространстве, вектора 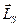 и
и 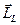 должны прецессировать вокруг
должны прецессировать вокруг 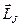 . Следовательно, прецессируют и полные механический и магнитный моменты. Из рисунка 55 видно,
. Следовательно, прецессируют и полные механический и магнитный моменты. Из рисунка 55 видно, 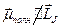 и прецессирует вокруг оси
и прецессирует вокруг оси 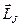 .
. 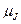 – проекция
– проекция 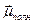 на
на 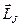 и
и 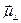 . Для достаточно большого промежутка времени среднее значение
. Для достаточно большого промежутка времени среднее значение 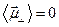 , поэтому
, поэтому
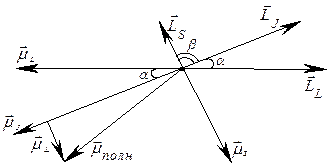
|
| Рис. 55 |
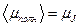 . Таким образом, если на языке моментов описывать магнитоэлектрические (оптические) эффекты, можно пользоваться
. Таким образом, если на языке моментов описывать магнитоэлектрические (оптические) эффекты, можно пользоваться 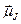 . Найдём связь между
. Найдём связь между 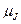 и
и 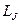 . Из рисунка 55 видно, что
. Из рисунка 55 видно, что 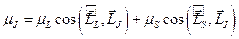 (1).
(1). 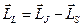 (2),
(2), 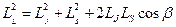 . Следовательно,
. Следовательно, 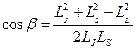 . Найдём
. Найдём 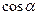 . Из уравнения (2) следует, что
. Из уравнения (2) следует, что 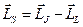 ,
, 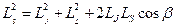 ;
; 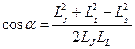 . Запишем уравнения для проекции магнитного момента на направление вектора
. Запишем уравнения для проекции магнитного момента на направление вектора 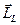 :
:
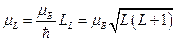
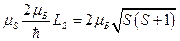 .
.
Подставим последние два выражения в (1) с учётом полученных выше выражений для косинусов:
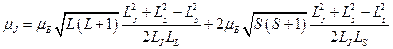
Подставим значения для каждого момента, выраженное через квантовые числа:
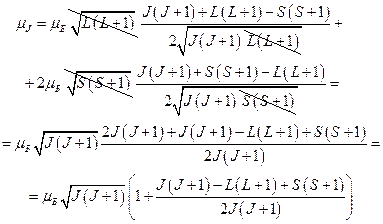
Выражение , помещённое в круглых скобках, называется фактором Ланде: 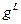 . Таким образом,
. Таким образом, 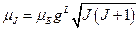 (3). Выражение (3) аналогично тому, которое связывает спиновой орбитальный момент с орбитальным механическим. Из этой аналогии следует смысл фактора Ланде – это гиромагнитное отношение для полного магнитного момента. В частности, получается, что если спиновое квантовое число равно нулю, то
(3). Выражение (3) аналогично тому, которое связывает спиновой орбитальный момент с орбитальным механическим. Из этой аналогии следует смысл фактора Ланде – это гиромагнитное отношение для полного магнитного момента. В частности, получается, что если спиновое квантовое число равно нулю, то 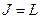 , тогда
, тогда 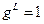 . Если же магнитный момент обусловлен спиновым движением, то есть
. Если же магнитный момент обусловлен спиновым движением, то есть 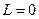 , то
, то 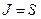 , а
, а 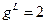 .
.
§ 5.7. Магнитомеханические эффекты.
В предыдущем параграфе мы показали, что существует связь между полным магнитным и механическим моментами. Если ориентация магнитного момента в пространстве, изменяется, то, чтобы выполнялось соотношение (3) предыдущего параграфа: 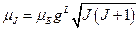 , должна изменяться ориентация механического момента. Явления, обусловленные связью механического и магнитного моментов, называют магнитомеханическими эффектами.
, должна изменяться ориентация механического момента. Явления, обусловленные связью механического и магнитного моментов, называют магнитомеханическими эффектами.
Пусть некоторый магнетик намагничен. Это значит, что все магнитные моменты атомов ориентированы в направлении намагничивания. Это приводит к тому, что и все механические моменты атомов будут стремиться ориентироваться определённым образом: 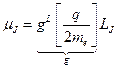 ,
, 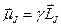 , где
, где 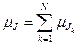 ,
, 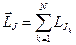 . Итак, при изменении магнитного момента образца, изменяется его механический момент так, чтобы их сумма всегда оставалась постоянной. Это значит, что при намагничивании образца он приобретёт дополнительный момент импульса. Для обнаружения магнитомеханических эффектов Эйнштейном и де Гаазом на тонкой упругой нити подвешивался цилиндр. Его помещали в
. Итак, при изменении магнитного момента образца, изменяется его механический момент так, чтобы их сумма всегда оставалась постоянной. Это значит, что при намагничивании образца он приобретёт дополнительный момент импульса. Для обнаружения магнитомеханических эффектов Эйнштейном и де Гаазом на тонкой упругой нити подвешивался цилиндр. Его помещали в

|
| Рис. 56 |
продольное магнитное поле, которое создавалось соленоидом, охватывающим образец. Магнитный и механический моменты связаны соотношением: 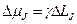 .
. 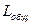 – полный механический момент образца. Так как образец изолирован, то закон сохранения момента импульса должен выполнятся. Полный момент импульса будет складываться из механического момента образца полного собственного механического момента всех электронов:
– полный механический момент образца. Так как образец изолирован, то закон сохранения момента импульса должен выполнятся. Полный момент импульса будет складываться из механического момента образца полного собственного механического момента всех электронов: 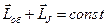 . Тогда,
. Тогда, 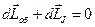 ,
, 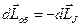 . Переходя к конечным приращениям, получим
. Переходя к конечным приращениям, получим 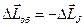 . Но
. Но 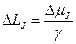 . Поэтому
. Поэтому 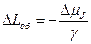 . Момент импульса образца равен
. Момент импульса образца равен 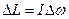 , где
, где 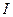 – момент инерции. Кинетическая энергия вращательного движения твёрдого тела, как известно из механики, равна:
– момент инерции. Кинетическая энергия вращательного движения твёрдого тела, как известно из механики, равна: 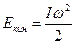 , а её изменение –
, а её изменение – 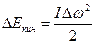 .
.
Обозначим 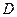 модуль упругости нити. Тогда при её закручивании на угол
модуль упругости нити. Тогда при её закручивании на угол 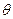 потенциальная энергия нити будет
потенциальная энергия нити будет 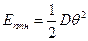 . По закону сохранения энергии
. По закону сохранения энергии 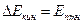 ,
, 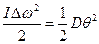 ,
, 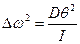 . Если
. Если 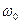 – собственная частота колебания образца, то она связана с модуле упругости кручения нити и моментом инерции следующим соотношением:
– собственная частота колебания образца, то она связана с модуле упругости кручения нити и моментом инерции следующим соотношением: 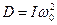 . Следовательно,
. Следовательно, 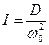 . Тогда,
. Тогда, 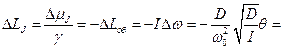
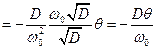 , т. о. Зная модуль упругости нити, собственную частоту колебаний образца и угол закручивания нити можно определить
, т. о. Зная модуль упругости нити, собственную частоту колебаний образца и угол закручивания нити можно определить 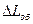 , а значит и
, а значит и 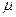 . Эйнштейн и де Гааз получили, что ферромагнитных цилиндров
. Эйнштейн и де Гааз получили, что ферромагнитных цилиндров 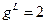 . Это значит1, что магнетизм обусловлен спиновым движением электронов.
. Это значит1, что магнетизм обусловлен спиновым движением электронов.
Эффектом обратным эффекту Эйнштейна – де Гааза является эффект Барнета. Рассмотрим поведение атома в магнитном поле. На магнитный момент 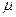 атома в этом поле действует момент сил:
атома в этом поле действует момент сил: 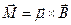 . Но атом обладает механическим моментом и поэтом ведёт себя как гироскоп. Под влиянием этого момента силы, будет задаваться
. Но атом обладает механическим моментом и поэтом ведёт себя как гироскоп. Под влиянием этого момента силы, будет задаваться 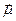 . Чтобы соотношение
. Чтобы соотношение
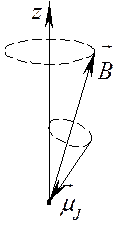
|
| Рис. 57 |
Между ними сохранялось, будет происходить прецессия механического момента атома вокруг заданного направления (не вокруг 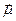 !!!). Это направление будет направлением вектора
!!!). Это направление будет направлением вектора 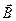 . По
. По
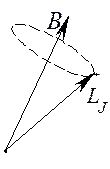
|
| Рис. 58 |
второму закону Ньютона для проекций векторов мы можем записать: 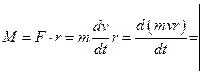 так как
так как 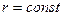
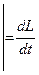 . В векторной форме
. В векторной форме 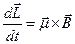 . Но
. Но 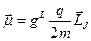 . Тогда
. Тогда 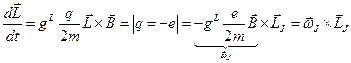 , где
, где 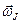 – частота прецессии механического момента вокруг направления магнитного поля. Если фактор Ланде для атома равен
– частота прецессии механического момента вокруг направления магнитного поля. Если фактор Ланде для атома равен 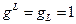 , то есть магнетизм атома обеспечивает орбитальный магнитный момент электронов (спин равен нулю), то
, то есть магнетизм атома обеспечивает орбитальный магнитный момент электронов (спин равен нулю), то 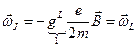 , то есть частота прецессии равна прецессии орбитального момента:
, то есть частота прецессии равна прецессии орбитального момента: 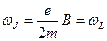 – ларморовой частоте прецессии. Благодаря прецессии всех атомов в магнитном поле в одном и том же направлении возникает дополнительный магнитный момент, что приводит к намагничиванию образца. В этом состоит суть эффекта Барнета.
– ларморовой частоте прецессии. Благодаря прецессии всех атомов в магнитном поле в одном и том же направлении возникает дополнительный магнитный момент, что приводит к намагничиванию образца. В этом состоит суть эффекта Барнета.
§ 5.8. Экспериментальные методы определения магнитного момента.
1. Опыт Штерна – Гербаха.
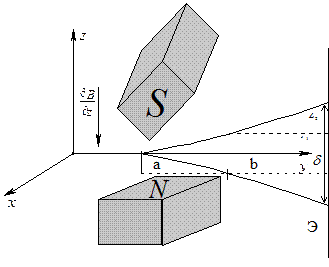
В 1921 году Штерн предложил опыт по измерению магнитного момента атома, который и реализовал с Гербахом в 1922 году. Суть опыта заключалась в следующем. Пучки нейтральных
|
| Рис. 59 |
атомов пропускались через область в которой создавалось неоднородное магнитное поле. В нём двигались атомы. На экране Э наблюдалось расщепление пучка на две части. Первые опыты проводились с атомами серебра. Для одного внешнего электрона имеем: 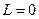 ,
, 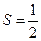 и
и 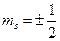 . Тогда
. Тогда 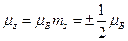 . Введём вектор
. Введём вектор 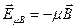 . Тогда на магнитный момент будет действовать сила
. Тогда на магнитный момент будет действовать сила 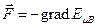 , сила, действующая вдоль оси
, сила, действующая вдоль оси 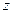 :
: 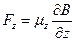 . Вычислим смещение атома под действием силы
. Вычислим смещение атома под действием силы 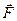 вдоль оси
вдоль оси 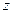 . По законам кинематики имеем:
. По законам кинематики имеем: 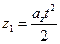 , где
, где 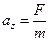 . С учётом того, что
. С учётом того, что 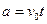 выражение для
выражение для 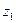 принимает вид:
принимает вид: 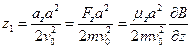 . Из рисунка 59 видно, что
. Из рисунка 59 видно, что 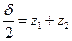 (1). Найдём
(1). Найдём 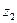 .
. 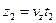 ,
, 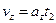 ,
, 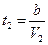 . Подставим в (1) выражения для
. Подставим в (1) выражения для 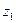 и
и 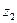 :
: 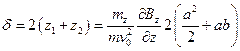 . Найдём из этой формулы
. Найдём из этой формулы 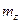 :
: 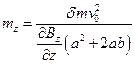 . Направление силы зависит от значения проекции магнитного момента. Так как значение проекции магнитного момента может принимать как положительные, так и отрицательные значения, то и сила будет действовать то вверх, то вниз. Число компонент, на которые расщепится пучок, зависит от проекции магнитного момента. Зная величину расщепления и значение
. Направление силы зависит от значения проекции магнитного момента. Так как значение проекции магнитного момента может принимать как положительные, так и отрицательные значения, то и сила будет действовать то вверх, то вниз. Число компонент, на которые расщепится пучок, зависит от проекции магнитного момента. Зная величину расщепления и значение
