ТЕОРИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛЦ

Важным разделом в ЛЦ являются методы анализа переходных процессов. На заре зарождения теории электрических цепей стало очевидным, что переход от одного установившегося режима к другому происходит не сразу. Наличие в электрических цепях конденсаторов и индуктивных элементов, заряды и потокосцепления которых не могут изменяться скачкообразно, приводит к тому, что становление нового режима происходит по мере изменения энергии ЭМП в этих элементах. В классической постановке задачи анализ переходных процессов в цепях сводится к нахождению полного решения системы интегродифферециальных уравнений и с этой точки зрения является традиционной. По мере развития теории дифференциальных уравнений этот подход обогащался различными методами нахождения частных решений исходной системы уравнений. Важным следует считать предложенное в 1853 г. Дюамелем выражение для исследования динамики линейных систем, позволяющее применительно к линейным электрическим цепям, для которых применим принцип наложения, по известной переходной или импульсной характеристике электрической цепи отыскать ее реакцию на воздействие произвольной формы, названное в его честь интегралом Дюамеля, или интегралом свертки. Интеграл Дюамеля по праву считается одной из основных формул в теории цепей. Обобщение интеграла Дюамеля для систем уравнений Коши в случае переменных во времени параметров электрической цепи мало пригодно для нахождения аналитических решений. С самого начала применения классического общего подхода для решения задач теории цепей выявились и ограничения, связанные с отысканием корней полиномов для нахождения решения однородного дифференциального уравнения, частного решения неоднородного уравнения, и проблема определения неизвестных постоянных интегрирования. По этим причинам, а также и для упрощения получения исходной системы уравнений О. Хевисайдом в 1892 г. был предложен метод операторов и интегрального преобразования, позволяющий алгебраизировать и находить решение системы дифференциальных уравнений. Впоследствии Д. Карсоном, Б. Ван‑дер‑Полем, Т. Бромвичем и др. было показано, что преобразование, лежащее в основе этого метода, является одной из множества модификаций преобразования П.Лапласа (1749–1827 гг.), предложенного им в 1779 г. Однако именно О. Хевисайду принадлежит заслуга внедрения этого метода решения системы дифференциальных уравнений в электротехнику. Этот метод с середины 20‑х годов нашел широкое распространение в теории переходных процессов. В теории линейных цепей особое место занимает проблема нахождения частного решения исходной неоднородной системы дифференциальных уравнений, описывающего установившийся процесс.

Работы К.С. Демирчяна, П.А. Бутырина позволили установить, что преобразование Лапласа со сдвигом во времени, представляющее собой установившуюся реакцию системы с импульсной переходной функцией вида e^pt на воздействие f(t) , порождается интегралом Дюамеля для бесконечного интервала времени, т.е.

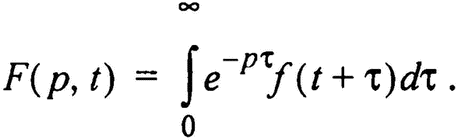
Такое преобразование позволяет получить решение для установившегося процесса непосредственно через изображение задающей функции F(p,t ), которая для данного преобразования является функцией времени. Если система дифференциальных уравнений записана относительно переменных состояний в виде матричного уравнения dx/dt = Ax + f (t) и изображение f(t) имеет вид F(p,t), то решение для установившегося процесса для системы уравнений состояний можно записать в виде х_уст = – F(A, t), и тогда полное решение системы дифференциальных уравнений будет иметь вид x(t) = e^At[x(0) + F(A,0)] – F(A,t)]. Такой подход позволяет исключить трудоемкий процесс обратного преобразования Лапласа для нахождения оригинала x(t) изображения X(p) и установить непосредственную взаимосвязь между интегралом Дюамеля и преобразованием Лапласа со сдвигом. Применение этого подхода в случае электрических цепей с периодически изменяющимися параметрами позволяет в ряде случаев (например, электрические машины) отыскать аналитические решения (П.А. Бутырин). Решение дифференциальных уравнений может быть найдено не только на основе преобразования Лапласа или Фурье (где в качестве ядра интегрального преобразования использована экспоненциальная (Лаплас) или тригонометрическая (Фурье) функция), но и других видов функций. В этом отношении методы на основе представления входящих в дифференциальные уравнения функций при помощи степенных рядов Тейлора (Г.Е. Пухов) являются оригинальными. Преимуществом этого метода является возможность его использования и для случая нелинейных уравнений.

В СССР теория переходных процессов начала привлекать внимание в связи с быстрым развитием электроэнергетики и расширением прикладных областей применения электрических цепей в приводе, электротермии, связи, автоматическом управлении и др. Важным этапом для развития исследований в этой области явилось появление работ Р. Рюденберга, К.А. Круга, молодых ученых A.M. Данилевского и A.M. Эфроса, погибших во время Великой Отечественной войны, и многих специалистов в области математики. 40–50‑е годы стали новым этапом развития теории переходных процессов. Была разработана теория, предложены критерии и методы подобия для физического и математического моделирования переходных процессов в сложных системах с электромеханическими преобразователями энергии (М.П. Костенко, Л.Р. Нейман, В.А. Веников). Развитие ЕЭС потребовало разработки теории переходных процессов в электрических цепях, содержащих электрические машины и линии с распределенными параметрами, которые существенным образом влияют на перенапряжения в системах (М.В. Костенко, С.А. Ульянов, Л.Г. Мамиконянц, К.П. Кадомская, М.Л. Левинштейн, В.В. Бушуев, Ч.М. Джуварлы, Л.А. Жуков, Ю.Г. Шакарян, В.В. Постолатий и др.).

Наряду с классическим и операторным методами широкое распространение получил частотный, или спектральный метод расчета переходных процессов. В течение 1950–1970 гг. частотные методы получили широкое внедрение в расчетную практику благодаря возможности экспериментального определения спектра частот входных и передаточных функций реальных устройств. Частотные характеристики ЛЦ полностью характеризуют поведение цепи, поскольку они зависят от ее инерционных свойств (наличия индуктивных и емкостных элементов) и от интенсивности рассеяния энергии ЭМП (наличия резистивных или эквивалентных им элементов) в ней. Поскольку любое воздействие может быть представлено своим спектром частот, то знания частотных свойств цепи достаточно, чтобы выяснить реакцию цепи на интересующее воздействие. Специфичными для этого метода оказались расчетные приемы, позволяющие описать переходные процессы на основе частотных характеристик цепи и воздействующих на нее возмущений. Частотные характеристики электротехнических устройств требовали особенно глубокого изучения в области автоматики и управления, усилительной техники и электросвязи. Поэтому именно в этих областях впервые с исчерпывающей полнотой была установлена зависимость между переходными процессами и частотными характеристиками и были разработаны методы расчета этих процессов. Этим вопросам в советской научной литературе уделялось большое внимание. Спектральные характеристики анализировались многими учеными, в том числе Л.И. Мандельштамом, Б.В. Булгаковым, А.А. Харкевичем, А.А. Вороновым, Г.А. Атабековым, В.В. Солодовниковым, В.А. Тафтом, И.С. Гоноровским, П.Н. Матхановым, Г. Боде, Э.А. Гиллемином, Дж. Карсоном и др. В практику расчета и проектирования электромагнитных процессов в электрических машинах большой вклад в части использования частотных методов внесли Я.М. Казовский, А.И. Важное, И.З. Богуславский и др. Использование частотных методов оказалось особенно продуктивным при анализе устойчивости состояния линеаризированных систем. Проблема устойчивости возникала также для систем с обратными связями. В этой связи следует отметить работы X. Найквиста (1932 г.), Г. Боде, Я.З. Цыпкина, А.В. Михайлова, который установил новый критерий устойчивости системы, и В.В. Солодовникова, предложившего замечательный по своей простоте и точности метод приближенного расчета переходных процессов по частотным характеристикам. Этот метод, известный как метод трапеций, получил широкое распространение в СССР.

В теории переходных процессов в последние десятилетия важное место заняли проблемы, связанные с протеканием процессов при наличии помех и под воздействием сил, носящих случайный или хаотический характер. Важность выяснения особенностей протекания таких процессов связана с повышением точности расчетных методов, с одной стороны, и необходимостью выделения полезной информации при выполнении полевых измерений в целях диагностики реального состояния исследуемой системы или устройства – с другой. Особое значение эта проблема приобретает при регулировании процессов в сложных электрических системах в реальном масштабе времени (Ю.Н. Руденко, Ф. Швепп, Д.В. Ром, А.З. Гамм, Л.А. Крумм, В.А. Баринов, С.А. Совалов и др.).