Переосмысление метода 1 страница
К концу XVI в. аристотелевой модели научного исследования был брошен решительный вызов. Стало естественным искать новые пути к методу сбора достоверных знаний о природе. Среди ученых, пытавшихся сформулировать новый научный подход, особенно известны две фигуры: Фрэнсис Бэкон и Рене дю Перрон Декарт. По моему мнению, важность этих двух людей для научной революции сильно переоценена.
Фрэнсис Бэкон родился в 1561 г. Его отцом был Николас Бэкон, лорд‑хранитель печати Великобритании. Получив образование в Тринити‑колледже в Кембридже, Фрэнсис получил право адвокатской практики в суде, где начал работать, затем продолжил свою карьеру в юриспруденции, дипломатии и политике. В 1618 г. он стал бароном Веруламским и лорд‑канцлером Великобритании, а позже – виконтом Сент‑Олбанским. Но в 1621 г. Бэкона признали виновным в коррупции, и указом парламента ему было запрещено состоять на государственной службе.
Репутация Бэкона в истории науки во многом основана на его книге «Новый органон» («Новый инструмент, или Истинные указания для истолкования природы»), опубликованной в 1620 г. В этой книге Бэкон, который не был ни ученым, ни математиком, пишет о крайне эмпирической точке зрения на науку, отвергая не только Аристотеля, но также Птолемея и Коперника. Открытия должны делаться непосредственно путем тщательного беспристрастного наблюдения за природой, а не выводиться дедуктивным путем из основополагающих принципов. Также Бэкон отвергает любые исследования, если они не приносят немедленной практической пользы. В «Новой Атлантиде» он придумывает коллективный исследовательский институт под названием «Дом Соломона», работники которого посвятили бы себя сбору полезных фактов о природе. Предполагалось, что таким образом человечество достигнет господства над природой, утраченного после изгнания из рая. Бэкон умер в 1626 г. Существует история о том, что он умудрился и тут остаться верным эмпирическому методу познания природы – он заработал пневмонию, экспериментально изучая способы заморозки мяса.
Бэкон придерживался точки зрения, диаметрально противоположной Платону. Конечно, обе крайности ошибочны. Прогресс зависит и от наблюдения, и от эксперимента, которые служат основой для размышлений об общих принципах и дедуктивных выводов из этих принципов, которые могут быть проверены через новые наблюдения и эксперименты. Поиск знания с практической целью может служить ограничением для неконтролируемых домыслов, но понимание мира имеет свою ценность и само по себе, вне зависимости от того, ведет ли оно к непосредственной пользе. Ученые XVII и XVIII вв. апеллировали к Бэкону в противовес Платону и Аристотелю, в чем‑то примерно так же, как американский политик может апеллировать к Томасу Джефферсону при том, что на него никак не повлияло что‑либо из того, что Джефферсон сказал или сделал. Я не вижу ни одного ученого, чья работа в действительности изменилась к лучшему благодаря сочинениям Бэкона. Галилею был не нужен Бэкон, чтобы сказать, что необходимо начать проводить эксперименты, и, я думаю, точно так же он был не нужен Бойлю и Ньютону. За сто лет до Галилея другой флорентиец Леонардо да Винчи (1452–1519) ставил опыты с падающими телами, текущими жидкостями и многие другие{233}. Мы знаем об этой работе только по нескольким сочинениям в области живописи и движения жидкостей, которые были скомпилированы после смерти да Винчи, а также по его записным книжкам, которые время от времени обнаруживаются. Но если эксперименты Леонардо никак и не повлияли на прогресс науки, то по крайней мере они демонстрируют, что сама идея об опытах носилась в воздухе задолго до Бэкона.
Рене Декарт был во всех отношениях более значительной фигурой, чем Бэкон. Он родился в 1596 г. в семье французского аристократа‑судьи, так называемого «дворянина мантии»[18]. Рене получил образование в коллегии иезуитов города Ла‑Флеш, изучал юриспруденцию в Университете Пуатье и служил в армии Морица Нассауского, принца Оранского, во время войны за независимость в Голландии. В 1619 г. Декарт решил посвятить себя философии и математике и начал работать всерьез после 1628 г., когда поселился в Голландии.
Декарт изложил свои взгляды на механику в книге «Мир» (Le Monde), написанной в 1630‑х гг., но опубликованной только в 1664 г., после его смерти. В 1637 г. он опубликовал свое философское сочинение «Рассуждение о методе, чтобы верно направлять свой разум и отыскивать истину в науках» (Discours de la méthode pour bien conduire sa raison, et chercher la vérité dans les sciences). Идеи, изложенные в этой работе, были развиты в самой длинной книге Декарта «Первоначала философии», опубликованной на латыни в 1644 г., а в переводе на французский – в 1647 г. В этих работах он высказывает скептическое отношение к знанию, полученному от авторитетов или чувственным путем. Для Декарта единственное достоверное доказательство того, что он существует, проистекало из наблюдения за тем, что он думает об этом. Далее он приходит к выводу о том, что мир существует, поскольку он сам может воспринимать его без какого‑либо усилия воли. Декарт отвергает телеологию Аристотеля – вещи являются тем, что они есть, независимо от целей, которым они служат. Он приводит несколько доказательств существования Бога (все неубедительные), но отвергает власть какой‑либо организованной религии. Также Декарт отвергает действие сверхъестественных сил на расстоянии – вещи взаимодействуют друг с другом путем непосредственных толчков и тяги.
Декарт очень много сделал для внедрения математики в физику, но, как и Платон, он был слишком увлечен достоверностью математических доказательств. В части I «Первоначал философии», озаглавленной «Об основах человеческого познания», Декарт описывает, как фундаментальные научные принципы могут быть с достоверностью выведены из чистой мысли. Мы можем доверять «естественному свету относительно тех атрибутов Бога, известное познание которых он пожелал нам дать», потому что «полностью немыслимо, чтобы он вводил нас в заблуждение»{234}. Странно, что Декарт думал, что Бог, который позволил случаться землетрясениям и эпидемиям чумы, не решился бы обмануть философа.
Декарт принимал мысль о том, что приложение фундаментальных физических принципов к отдельным системам может оказаться недостоверным и потребовать проведение экспериментов, если ученому неизвестны все детали, из которых состоит система. В своих дискуссиях по астрономии в части III «Первоначал философии» он рассматривает различные гипотезы строения планетной системы и приводит замечания Галилея по наблюдению фаз Венеры как причину предпочесть гипотезы Коперника и Браге гипотезе Птолемея.
Это краткое изложение показывает взгляды Декарта только в самых общих чертах. Его философией всегда восхищались и восхищаются сейчас, особенно специалисты‑философы и французы. Меня это ставит в тупик. Просто поразительно, как часто для человека, заявляющего, что он нашел самый лучший метод получения достоверных знаний, Декарт был не прав, говоря о различных явлениях природы. Он был не прав, говоря, что Земля имеет продолговатую форму (то есть расстояние вдоль линии, соединяющей полюсы, больше длины экватора). Он, как и Аристотель, ошибался, утверждая, что вакуум не существует. Он был не прав, доказывая, что свет передается мгновенно{235}. Он ошибался по поводу того, что космос наполнен материальными вихрями, которые передвигают планеты вдоль их траекторий. Он был не прав по поводу шишковидной железы, которая является вместилищем души и отвечает за человеческую совесть. Он ошибался насчет того, что́ именно сохраняется при соударениях предметов. Он был не прав насчет того, что скорость свободного падения пропорциональна пройденному расстоянию. И, в конце концов, основываясь на наблюдении за поведением нескольких любимых домашних котов, я убежден, что Декарт ошибался и насчет того, что животные – это машины, которые не имеют души. У Вольтера были точно такие же сомнения по поводу Декарта:
«Он ошибался по поводу природы души, по поводу доказательств существования Бога, по поводу материи и законов движения, а также относительно природы света; он допускает врожденные идеи, открывает новые элементы, творит мир, преобразует человека на свой собственный лад, и потому справедливо говорят, что человек Декарта на самом деле и есть всего лишь его человек, весьма далекий от человека подлинного»{236}.
Научные заблуждения Декарта не имели бы особого значения, если бы речь шла о работах по этической или политической философии или даже метафизике, но для человека, который писал о «методе, позволяющем направлять свой разум и отыскивать истину в науках», постоянные ошибки не могут не бросать тень на философское суждение. Дедукция просто не может вынести тот груз, который Декарт взвалил на нее.
Даже самые великие ученые ошибаются. Мы уже видели, как Галилей ошибался насчет приливов и комет, и мы увидим, как Ньютон ошибся по поводу дифракции. Но, несмотря на все свои ошибки, Декарт, в отличие от Бэкона, внес значительный вклад в науку. Он содержится в трех приложениях к «Рассуждению о методе» под заголовками «Геометрия», «Оптика» и «Метеорология»{237}. С моей точки зрения, именно эти труды, а не его философские сочинения, являются вкладом Декарта в науку.
Самым большим достижением Декарта было изобретение нового математического метода, который теперь называется аналитической геометрией, где кривые и плоскости представлены в виде уравнений, которым удовлетворяют координаты точек, принадлежащих кривой или плоскости. «Координатами», в общем, могут быть любые числа, которые определяют местоположение точки, – например, долгота, широта, высота над уровнем моря, – но обычно используют декартовы координаты , определяемые расстоянием от точки до некоторого центра и измеряемые вдоль каких‑либо взаимно перпендикулярных направлений. Например, в аналитической геометрии круг радиусом R – это кривая, на которой координаты х и у находятся на определенном расстоянии от центра, совпадающего с пересечением двух перпендикулярных прямых, и удовлетворяют равенству x ² + y ² = R ² (в техническом замечании 18 дается подробное описание эллипса). Это очень важное использование букв алфавита, чтобы обозначить неизвестное расстояние или неизвестную величину, берет свое начало в работах французского математика, придворного и специалиста по шифрам XVI в. Франсуа Виета, но Виет еще записывал равенства словами. Современной формой алгебры и ее приложению к аналитической геометрии мы обязаны Декарту.
Используя аналитическую геометрию, мы можем найти координаты точки, где две кривые пересекаются, или получить уравнение кривой, образующейся на пересечении двух поверхностей. Для этого мы должны решить пару уравнений, которые определяют кривые или поверхности. Сегодня большинство физиков решают геометрические задачи именно таким образом, используя аналитическую геометрию, а не классические методы Евклида.
В физике Декарт внес значительный вклад в изучение света. Вначале в «Диоптрике» он описал соотношение между углами падения и преломления света на границе среды А и среды В (например, воздуха и воды): если угол между падающим лучом и перпендикуляром к поверхности среды обозначить как i , а угол между преломленным лучом и этим перпендикуляром – как r , то синус угла{238} i , деленный на синус угла r , равен независимой от значения величин углов постоянной n :
sin i /sin r = n.
В общем случае, где средой А является воздух (или, строго говоря, пустота), n – это постоянная, которая называется показателем преломления для среды B . Например, если А – это воздух, а В – вода, то n – это показатель преломления воды, который равен примерно 1,33. В любом подобном случае, когда n больше единицы, угол преломления r меньше угла падения i , и луч света, входя в более плотную среду, преломляется, приближаясь к направлению перпендикуляра к поверхности.
Декарт не знал, что то же самое соотношение было в 1621 г. выведено эмпирическим путем голландцем Виллебрордом Снеллиусом, а еще раньше – англичанином Томасом Хэрриотом, а в рукописи Х в. арабского физика ибн Сахля предполагается, что об этом законе уже известно, но Декарт был первым, кто опубликовал это открытие. Сегодня это соотношение во всем мире называют законом Снеллиуса (кроме Франции, где его авторство принято приписывать Декарту).
За доказательством закона преломления Декарта проследить очень трудно, отчасти потому, что он ни в своем описании доказательства, ни в изложении результата не пользовался тригонометрическими понятиями вроде синуса угла, а писал чисто в геометрических терминах, хотя, как мы уже видели ранее, аль‑Баттани, чьи работы были хорошо известны в средневековой Европе, заимствовал синус у индийских математиков еще за семь столетий до Декарта. Вывод закона преломления у Декарта основывается на придуманной им аналогии с теннисным мячиком, который разрывает тонкую ткань. Мячик теряет часть своей скорости, но ткань не оказывает никакого эффекта на ту составную часть общей скорости, которая направлена параллельно ткани. Как показано в техническом замечании 27, это допущение привело к результату, о котором мы говорили выше: отношение синусов углов между прямыми, по которым мячик движется к экрану и от него, и перпендикуляра к этому экрану составляет не зависящую от величин углов постоянную n . Хотя в описании Декарта результат увидеть очень трудно, должно быть, он понимал, что у него все верно получилось, потому что, подобрав соответствующие значения для n , дал более‑менее правильные численные ответы в теории о радуге, о которой мы поговорим ниже.
В выводе закона преломления Декарт совершенно точно ошибался в двух вещах. Очевидно, что свет – это не теннисный мячик, а поверхность, разделяющая воздух и воду или стекло, – не тонкая ткань, так что очень сомнительно, что эта аналогия уместна, особенно для Декарта, который считал, что свет, в отличие от теннисного мячика, движется с бесконечной скоростью{239}. К тому же аналогия Декарта ведет к неправильной оценке величины n . Как показано в техническом замечании 27, для теннисных мячиков его допущение предполагает, что n равно отношению скорости мяча vB в среде B (после того, как он пройдет сквозь экран) к скорости vA в среде A (до того, как он ударит по экрану). Конечно, проходя сквозь экран, мяч замедлится, поэтому скорость vB будет меньше скорости vA и их отношение n будет меньше единицы. Если это приложить к свету, то получится, что угол между преломленным лучом и перпендикуляром будет больше , чем угол между падающим лучом и перпендикуляром. Декарт знал об этом и даже снабдил объяснение диаграммой, показывающей, как движение теннисного мячика отклоняется от перпендикуляра в сторону большего угла. Декарт также знал, что для света это неверно, поскольку еще со времен Птолемея наблюдали, что луч света, проходящий из воздуха в водную среду, преломляется по направлению к перпендикуляру к поверхности воды, поэтому синус i больше, чем синус r , и, следовательно, n больше единицы. В чрезвычайно запутанном объяснении, которого я не понимаю, Декарт каким‑то образом доказывает, что свет легче проходит через воду, чем через воздух, поэтому для света n больше единицы. Для задачи Декарта невозможность объяснить, откуда он берет значение n , на самом деле не имела значения, потому что он мог получить – и на самом деле получил – значения n из экспериментов (возможно, из данных, которые были в «Оптике» Птолемея), и эти значения, конечно, были больше единицы.
Более убедительное доказательство закона преломления дал математик Пьер де Ферма (1601–1665). Он сделал его по образцу доказательства правила равенства углов падения и отражения Герона Александрийского, но основывался на предположении о том, что лучи света проходят свой путь за наименьшее время, а не проходят наименьшее расстояние. Как показано в техническом замечании 28, это предположение приводит к правильной формуле, где n – это отношение скорости света в среде А к его скорости в среде В и, таким образом, больше единицы, если А – это воздух, а В – вода или стекло. Декарт никогда не смог бы вывести такую формулу для n , поскольку для него свет двигался мгновенно (как мы увидим в главе 14, другое доказательство с правильным результатом было дано Христианом Гюйгенсом. Оно было основано на теории Гюйгенса о том, что свет – это движущееся волновое возмущение среды, и не нуждается в априорном предположении Ферма о том, что свет проходит свой путь за наименьшее возможное время).
Декарт сделал великолепное дополнение к закону преломления: в своей «Метеорологии» он использовал соотношение между углами падения и преломления, чтобы объяснить появление радуги. Это было величайшее достижение Декарта как ученого. Аристотель доказывал, что цвета радуги получаются, когда свет отражается от капель воды, рассеянных в воздухе{240}. Так же, как мы уже видели в главах 9 и 10, в Средние века и аль‑Фариси, и Дитрих из Фрайбурга считали, что радуга получается, когда свет преломляется, проходя через капли воды, взвешенные в воздухе. Но до Декарта никто не представлял детально численного описания того, как это происходит.
Вначале Декарт провел эксперимент, используя стеклянный сосуд сферической формы с тонкими стенками, наполненный водой, в качестве модели капли дождя. Он заметил, что, когда лучи света проходят сквозь шар в разных направлениях, свет, который выходит обратно под углом примерно 42° к углу падения, становится «полностью красным и несравнимо более ярким, чем остальные лучи». Он пришел к заключению, что радуга (или, по крайней мере, ее красный цвет) образует в небе арку, когда угол между направлением на радугу и направлением от нее на солнце равен примерно 42°. Декарт предположил, что лучи света преломляются, попадая в каплю воды, отражаются от ее внутренней поверхности и затем снова преломляются, когда попадают из капли в воздух. Но как объяснить свойство радуги посылать лучи из капель именно под углом в 42° к направлению их падения?
Чтобы ответить на этот вопрос, Декарт предполагает, что лучи света попадают в сферическую каплю по десяти различным параллельным направлениям. Он присвоил каждому из этих лучей то, что сегодня называют прицельным параметром b – величина кратчайшего расстояния до центра капли, на котором луч прошел бы, если бы проходил сквозь каплю прямо, не преломляясь. Первый луч был выбран так, что если бы он не преломлялся, то прошел бы на расстоянии от центра капли, равном 10 % радиуса R капли (то есть b = 0,1R ). При этом десятый луч был выбран так, чтобы задеть поверхность капли по касательной (b = R ). Все остальные лучи были равномерно распределены между ними. Декарт описал путь каждого луча, как он преломился, войдя внутрь капли, отразился от ее внутренней поверхности и снова преломился, покидая каплю, используя закон равенства углов отражения Евклида и Герона и свой собственный закон преломления, приняв показатель преломления воды n за 4/3. В таблице приводятся значения, полученные Декартом для угла φ между выходящим из капли лучом и направлением его падения для каждого луча, и результаты моих собственных расчетов, при которых я использовал тот же самый показатель преломления:
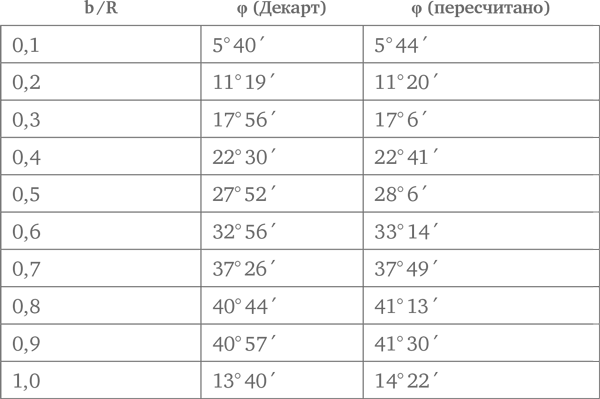
Неточность некоторых результатов Декарта может быть связана с ограниченностью математических средств в то время. Я не знаю, была ли у него возможность пользоваться таблицей синусов, но у него точно не было ничего, хотя бы отдаленно напоминающего современный микрокалькулятор. Тем не менее эти результаты выглядели бы лучше, если бы Декарт округлил их до ближайшего целого градуса, а не до 10 минут угла.
Как заметил Декарт, угол φ близок к 40° для достаточно широкого диапазона прицельных расстояний b . Далее он повторил расчеты для восемнадцати еще более близко расположенных лучей, значения b для которых отличались от 80 до 100 % радиуса капли, при этом угол φ был равен примерно 40°. Декарт выяснил, что для четырнадцати из этих восемнадцати лучей угол φ находился в промежутке от 40° до максимальной величины 41° 30´. Таким образом, эти теоретические расчеты подтвердили его экспериментальные данные, упомянутые ранее, где угол наиболее яркого луча был округленно равен 42°.
В техническом замечании 29 приводится современный вариант расчетов Декарта. Вместо того чтобы высчитывать численное значение угла φ между входящим и исходящим лучом для каждого луча в совокупности лучей, как делал Декарт, выводится простая формула, по которой рассчитывается φ для любого угла, при любом прицельном расстоянии b и при любом значении n отношения между скоростью света в воздухе и скоростью света в воде. Затем эта формула используется для определения значения φ, при котором выходящие из капли лучи наиболее интенсивны{241}. Для n, равного 4/3, оптимальное значение φ оказывается 42°, при котором преломленный свет собирается, как это и определил Декарт. Декарт даже рассчитал соответствующий угол для вторичной радуги, которая производится светом, дважды отражающимся внутри капли до того, как покидает ее.
Декарт видел связь между разделением цветов, характерным для радуги, и цветами, получающимися при преломлении света через призму, но он не смог рассчитать количественные показатели этого явления, потому что не знал, что белый солнечный свет состоит из всех цветов и что показатель преломления света немного меняется в зависимости от его цвета. В действительности, тогда как Декарт брал показатель преломления для воды, равный 4/3 = 1,3333…, на самом деле для типичной длины волны красного цвета он равен скорее 1,330, а для синего – 1,343. Используя общую формулу, описанную в замечании 29, можно найти максимальное значение для угла φ между углом падения и преломления, которое будет равно 42,8° для красного цвета и 40,7° для синего. Именно поэтому Декарт и видел ярко‑красный цвет, когда смотрел на сосуд с водой под углом в 42° к направлению солнечных лучей. Это значение угла φ немного выше максимального значения 40,7° для синего цвета, поэтому Декарт не мог увидеть лучей из синей части спектра, но немного ниже максимального значения φ 42,8° для красного цвета, поэтому и мог получиться достаточно яркий оттенок красного.
Работа Декарта по оптике приближается к методу современной физики. Декарт сделал ни на чем не основанное предположение о том, что свет преодолевает границу между двумя средами так же, как теннисный мячик, прорывающий тонкий экран, и использовал его, чтобы вывести соотношение между углами падения и преломления, которое (при правильном выборе показателя преломления n ) согласуется с наблюдениями. Далее, используя сосуд, наполненный водой, в качестве модели капли дождя, Декарт провел наблюдения, подтвердившие возможное происхождение радуги. Затем он показал математически, что эти наблюдения следуют из его закона преломления. Он не понимал, почему у радуги возникают разные цвета, поэтому обошел этот вопрос и опубликовал то, что понимал. Это как раз то самое, что делают физики сегодня. Но если отвлечься от приложения математических расчетов к физической задаче, то какое отношение это исследование имеет к «Рассуждению о методе» Декарта? Я не вижу, чтобы он выполнял свои собственные предписания «четко следовать пути рассуждений и искать истину в науке».
Я должен добавить, что в «Первоначалах философии» Декарт предлагал значительное качественное улучшение понятия «импетус Буридана»{242}. Он доказывал, что «любое движение само по себе происходит вдоль прямых линий», поэтому (в противовес и Аристотелю, и Галилею) требуется сила, которая заставляет небесные тела двигаться по искривленным орбитам. Но Декарт не сделал никакой попытки рассчитать эту силу. Как мы увидим в главе 14, Гюйгенсу удалось найти формулу для силы, которая требуется, чтобы тело двигалось с заданной скоростью по кругу заданного радиуса, а Ньютон объяснил, что эта сила является силой тяготения.
В 1649 г. Декарт поехал в Стокгольм, чтобы стать учителем правящей королевы Кристины. Возможно, из‑за холодной шведской погоды Декарт в следующем году, как и Бэкон, умер от пневмонии. Четырнадцать лет спустя его работы были добавлены к книгам Коперника и Галилея в список литературы, запрещенной Римской католической церковью.
Сочинения Декарта по научному методу всегда привлекали внимание философов, но я не думаю, что они оказали большое влияние на практику научного исследования (и даже, как уже говорилось выше, на самую успешную научную работу самого Декарта). Его работы имели один негативный эффект – физика Ньютона была принята во Франции несколько позже. Алгоритм выведения научных принципов из чистых размышлений, описанный в «Рассуждении о методе», никогда не работал и не мог работать. Гюйгенс в молодости считал себя последователем Декарта, но позже пришел к пониманию того, что научные принципы – это только гипотезы, которые должны быть проверены сравнением их следствий с наблюдениями{243}.
С другой стороны, работа Декарта по оптике показывает, что он сам понимал, что научные гипотезы такого рода иногда необходимы. Лоренс Лаудан нашел подтверждение этого понимания в беседах Декарта по химии в «Первоначалах философии»{244}. Поэтому возникает вопрос, был ли в действительности хоть один ученый, который перенял от Декарта практику проверять придуманные гипотезы экспериментально, как думал Лаудан о Бойле. Я лично думаю, что эта практика была широко распространена и до Декарта. Как еще можно описать то, что делал Галилей, используя гипотезу о том, что падающие тела ускоряются равномерно, чтобы вывести из нее следствие о том, что брошенные тела летят по параболической траектории, а затем проверить ее экспериментально?
Согласно биографии Декарта, написанной Ричардом Уотсоном, «без картезианского метода разложения материальных вещей на первичные элементы мы никогда бы не изобрели атомную бомбу. Рост современной науки в семнадцатом веке, ее расцвет в восемнадцатом, промышленная революция в девятнадцатом, ваш персональный компьютер в двадцатом и расшифровка работы мозга в двадцать первом – все это картезианство»{245}. Декарт, безусловно, внес огромный вклад в развитие математики, но утверждать, что его сочинения по научному методу привели ко всем этим замечательным достижениям, абсурдно.
Декарт и Бэкон – это только два философа среди очень многих, которые на протяжении веков пытались определить правила научного поиска. Это никогда не срабатывает. Мы узнали, как вести научные исследования, не придумывая правила, как заниматься наукой, а исходя из опыта занятий наукой, руководствуясь ощущением удовлетворения, которое мы испытываем, когда наши методы позволяют нам что‑то объяснить.
Обобщения Ньютона
С Ньютоном мы подходим к кульминации научной революции. Но что за странный тип сыграл такую важную роль в истории науки! Ньютон никогда не покидал маленький район Англии, в который входили Лондон, Кембридж и его родная деревня в Линкольншире. Он даже никогда не видел моря, приливы и отливы которого так его интересовали. Достигнув средних лет, Ньютон не имел близких отношений ни с одной женщиной, и даже с матерью его отношения были прохладными{246}. Его очень волновали вопросы, не имеющие никакого отношения к науке, в том числе хронология Книги пророка Даниила. Каталог рукописей Ньютона, выставленный на продажу на аукционе «Сотби» в 1936 г., насчитывал 650 000 слов в текстах по алхимии и 1,3 млн слов в текстах по религии. С теми, кто казался ему соперником, Ньютон мог быть коварным и отвратительным. Тем не менее этот человек связал воедино физику, астрономию и математику, что не удавалось сделать философам со времен Платона.
Некоторые авторы настаивают, что Ньютон не был современным ученым. Среди этих заявлений хорошо известно высказывание Джона Мейнарда Кейнса, купившего на аукционе «Сотби» в 1936 г. некоторые бумаги Ньютона: «Ньютон не был первым человеком века разума. Он был последним из волшебников, вавилонян и шумеров, последним из великих умов, смотревших на внешний и внутренний мир теми же глазами, как и те, кто начал создавать наше научное наследие чуть ли не 10 000 лет тому назад»{247}. Но Ньютон не был просто талантливым пережитком магического прошлого. Не будучи ни волшебником, ни в полном смысле слова современным ученым, он пересек границу между натурфилософией прошлого и тем, что стало современной наукой. Достижения Ньютона, несмотря на все его недостатки, обеспечили парадигму, которой в дальнейшем следовали все ученые и благодаря которой наука стала современной.
Исаак Ньютон родился в рождественский день 1642 г. на семейной ферме в имении Вулсторп в Линкольншире. Его отец, неграмотный йомен (мелкий землевладелец), умер вскоре после рождения сына. У матери было более высокое положение в обществе, она была джентри (мелкопоместная дворянка), а ее брат закончил Кембриджский университет и стал священником. Когда Ньютону было три года, его мать снова вышла замуж и уехала из Вулсторпа, оставив сына на попечение бабушки. С десяти лет Ньютон посещал королевскую школу, занимавшую одну комнату в городке Грэнтем, в двенадцати километрах от Вулсторпа. Там он жил в доме местного аптекаря. В Грэнтеме он изучал латынь и теологию, арифметику и геометрию, немного греческий и древнееврейский.
Дата добавления: 2016-01-29; просмотров: 937;
