Метод дифференциальный.

Часто применяют для определения влияния различных составляющих величин на выходной сигнал, математически выраженный через величины, входящие в передаточную функцию.

Коэффициент влияния отыскивается как частная производная градуировочной характеристики идеальной измерительной цепи по соответствующему параметру.

;

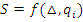g w:val="EN-US"/></w:rPr><m:t>n</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> ;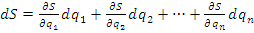

;

;

;

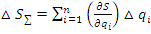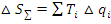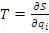Сущность дифференциального метода заключается в том, что составляются уравнения механизма, т.е. уравнения положения или перемещения ведомого звена в зависимости от координаты ведущего звена; затем дифференцированием его в частных производных, и полученный полный дифференциал есть ошибка положения или перемещения механизма.

Коэффициент влияния определяет долю влияния конкретной погрешности на суммарную.

Достоинства метода:

1.Метод является универсальным, т.е. пригоден для исследования измерительных цепей, составленных из любых преобразовательных элементов.

2.Может быть использован при исследовании группы однородных механизмов.

3.Является самым точным

Недостатки метода:

1.Требует знания градуировочной характеристики

2.С помощью метода нельзя отыскать коэффициент влияния нулевых параметров.

Указанные недостатки дифференциального метода ограничивают его применение при исследовании измерительных устройств, в которых существенное значение имеют погрешности формы кинематических элементов, их взаимное положение, т.е. те факторы, которые формируют нулевые параметры.