Комплексный метод расчета.

Общие сведения

Комплексный метод расчета основан на представлении синусоидальных функций комплексными числами.

Если есть две синусоидальные функции одной частоты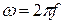

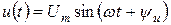и то они отличаются друг от друга парой чисел U_m, I_m – максимальными значениями и ψ_u, ψ_i – начальными фазами. Парой чисел определяются и комплексные числа

, где

– А – модуль комплексного числа,

– α – аргумент,

– – мнимая единица.

Эти свойства синусоидальных функций и комплексных чисел дают возможность представить (зашифровать) синусоидальною функцию комплексным числом. В этом случае в качестве модуля удобно брать действующие значения напряжения и тока и а аргументов их начальные фазы ψ_u, и ψ_i .

Тогда комплексы напряжения и тока, соответствующие синусоидальных u(t) и i(t) запишутся:

и .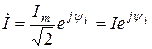

Правила перехода от синусоидальной функции к соответствующему комплексному числу можно представить так:

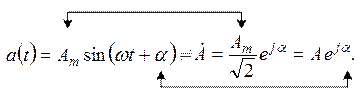
Также правила позволяют сформулировать свойства перехода от функций a(t) к их изображениям:

1. Операции сложения (вычитания) двух синусоидальных функций соответствует операция слоения (вычитания) соответствующих комплексов:

2. Операции умножения функции a(t) на число С соответствует умножение на это число комплекса

3. Операции дифференцирования функции a(t) соответствует умножение комплекса на jω

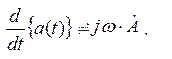
4. Операции интегрирования функции a(t) соответствует деление комплекса на jω

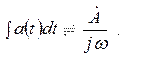
Эти свойства позволяют установить связь между комплексами тока и напряжения на идеальных элементах r, L, C и иллюстрировать эти соотношения на векторных диаграммах, построенных на комплексной плоскости.

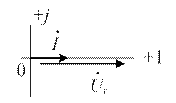
Резистивный элемент цепи r
	Этому элементу соответствует комплексная схема замещения
Индуктивность L
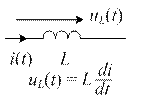
	Этому элементу соответствует комплексная схема замещения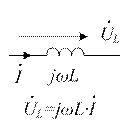
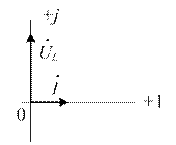
Электрическая емкость С
	Этому элементу соответствует комплексная схема замещения

Здесь во всех соотношениях принято, что начальная фаза тока ψ_i = 0.