Метод деформации профиля зеркала.
Сущность метода состоит в том, что зеркалу в вертикальной плоскости придают такую форму, при которой распределение потока мощности в угловом секторе [ 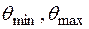 ] будет близким к заданному, определяемому соотношением (1.38). Очевидно, что для получения максимума излучения в направлении
] будет близким к заданному, определяемому соотношением (1.38). Очевидно, что для получения максимума излучения в направлении 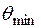 верхняя (над фокальной осью) часть зеркала должна иметь параболический профиль, а нижняя, формирующая АДН в области
верхняя (над фокальной осью) часть зеркала должна иметь параболический профиль, а нижняя, формирующая АДН в области 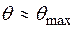 , – меньший, чем у параболы, радиус кривизны (рис. 1.29, а).
, – меньший, чем у параболы, радиус кривизны (рис. 1.29, а).

Рис. 1.29
Рассмотрим методику приближенного определения профиля на примере цилиндрического зеркала с линейным облучателем, базирующуюся на геометрической оптике (рис. 1.29, б).
Облучатель находится в фокусе F параболы, показанной пунктирной линией. На кривой профиля зеркала имеются две близкие точки –  и
и 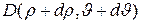 . Эта запись означает, что угол между лучами FC и FD составляет
. Эта запись означает, что угол между лучами FC и FD составляет 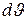 , а длины отрезков FC и FD различаются на величину
, а длины отрезков FC и FD различаются на величину 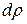 . Так как точки C и D близки друг к другу, то условно можно считать, что отрезок CD перпендикулярен нормали n0 в точке C. Лучи, отраженные от зеркала в точках C и D, образуют с фокальной осью углы q и q+dq, причем
. Так как точки C и D близки друг к другу, то условно можно считать, что отрезок CD перпендикулярен нормали n0 в точке C. Лучи, отраженные от зеркала в точках C и D, образуют с фокальной осью углы q и q+dq, причем 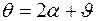 , где a – угол между нормалью n0 в точке C и падающим лучом. Опустим перпендикуляр СЕ на луч FD;при этом длина отрезка DE равна
, где a – угол между нормалью n0 в точке C и падающим лучом. Опустим перпендикуляр СЕ на луч FD;при этом длина отрезка DE равна 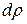 . В полученном прямоугольном треугольнике СЕD угол С равен углу a (как углы со взаимно перпендикулярными сторонами). Из треугольника СЕD, учитывая, что
. В полученном прямоугольном треугольнике СЕD угол С равен углу a (как углы со взаимно перпендикулярными сторонами). Из треугольника СЕD, учитывая, что  , определим:
, определим:
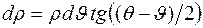 . (1.40)
. (1.40)
Отсюда находим дифференциальное уравнение профиля зеркала:
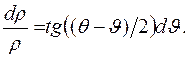 (1.41)
(1.41)
Интегрируя (1.41) от  до
до 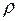 и от
и от 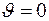 до
до 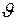 и замечая, что
и замечая, что 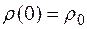 , получаем уравнение профиля зеркала:
, получаем уравнение профиля зеркала:
 (1.42)
(1.42)
Поскольку профиль зеркала отличен от параболического, то величина угла q зависит от положения точки С на зеркале, или угол q следует рассматривать как функцию угла визирования 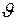 этой точки:
этой точки: 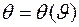 . Эту зависимость можно определить из требования получения заданной косекансной ДН
. Эту зависимость можно определить из требования получения заданной косекансной ДН 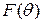 при известной диаграмме облучателя
при известной диаграмме облучателя 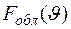 . Поскольку мощность падающей от облучателя волны в секторе
. Поскольку мощность падающей от облучателя волны в секторе 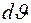 пропорциональна
пропорциональна 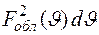 , а мощность волны, отраженной от зеркала, в секторе dq пропорциональна
, а мощность волны, отраженной от зеркала, в секторе dq пропорциональна 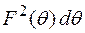 , то можно записать уравнение баланса мощностей:
, то можно записать уравнение баланса мощностей:
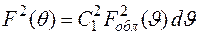 , (1.43)
, (1.43)
где С1 – коэффициент пропорциональности.
Проинтегрируем обе части этого уравнения, учитывая формулу (1.38):
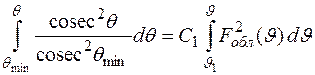 .
.
Отсюда
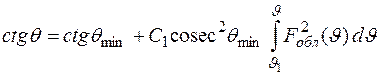 . (1.44)
. (1.44)
Константу С1 найдем с учетом соответствия углу 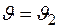 значения
значения 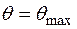 :
:
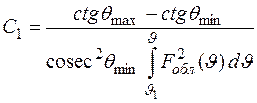 . (1.45)
. (1.45)
Метод деформации профиля зеркала позволяет получить гладкую косекансную ДН в секторе 60…70о без расширения диаграммы в горизонтальной плоскости. Однако такая конструкция существенно сложнее в реализации, особенно для больших зеркал.
Размер зеркала по вертикали при использовании обоих методов приближенно можно определить как
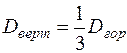 . (1.46)
. (1.46)
Дата добавления: 2016-01-29; просмотров: 2577;
