Электромагнитное взаимодействие. Роль системы отсчета. Закон Кулона.
Электромагни́тное взаимоде́йствие — одно из четырёх фундаментальных взаимодействий. Электромагнитное взаимодействие существует между частицами, обладающими электрическим зарядом[1]. С современной точки зрения электромагнитное взаимодействие между заряженными частицами осуществляется не прямо, а только посредством электромагнитного поля.
С точки зрения квантовой теории поля[2] электромагнитное взаимодействие переносится безмассовым бозоном — фотоном (частицей, которую можно представить как квантовое возбуждение электромагнитного поля). Сам фотон электрическим зарядом не обладает, но может взаимодействовать с другими фотонами путём обмена виртуальными электрон-позитронными парами.
Из фундаментальных частиц в электромагнитном взаимодействии участвуют также имеющие электрический заряд частицы: кварки, электрон, мюон и тау-лептон (изфермионов), а также заряженные калибровочные W±-бозоны. Остальные фундаментальные частицы Стандартной Модели (все типы нейтрино, бозон Хиггса и переносчики взаимодействий: калибровочный Z0-бозон, фотон, глюоны) электрически нейтральны.
Электромагнитное взаимодействие отличается от слабого[3] и сильного[4] взаимодействия своим дальнодействующим характером — сила взаимодействия между двумя зарядами спадает только как вторая степень расстояния (см.: закон Кулона). По такому же закону спадает с расстоянием гравитационное взаимодействие. Электромагнитное взаимодействие заряженных частиц намного сильнее гравитационного, и единственная причина, по которой электромагнитное взаимодействие не проявляется с большой силой в космических масштабах — электрическая нейтральность материи, то есть наличие в каждой области Вселенной с высокой степенью точности равных количеств положительных и отрицательных зарядов.
В классических (неквантовых) рамках электромагнитное взаимодействие описывается классической электродинамикой.
Свойства[править | править вики-текст]
В электромагнитном взаимодействии могут принимать участие только объекты, обладающие электрическим зарядом (в том числе и нейтральные в целом, но состоящие из заряженных частиц). Таковыми являются большинство известных фундаментальных элементарных частиц, в частности, все кварки, все заряженные лептоны(электрон, мюон и тау-лептон), а также заряженные калибровочные бозоны W±. По современным представлениям электромагнитное взаимодействие осуществляется через электромагнитное поле, кванты которого — фотоны — являются переносчиками электромагнитного взаимодействия[5].
В отличие от слабого и сильного взаимодействий электромагнитное взаимодействие так же, как и гравитационное, является дальнодействующим. В частности, сила притяжения неподвижных противоположно заряженных тел спадает на больших расстояниях степенным образом — по закону обратного квадрата (см. закон Кулона). Дальнодействие электромагнитных сил обусловлено отсутствием массы у фотонов как переносчиков этого взаимодействия[5].
В микромире интенсивность (эффективное сечение) электромагнитного взаимодействия характеризуется величиной постоянной тонкой структуры:
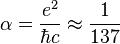 ,
,
где  — элементарный электрический заряд,
— элементарный электрический заряд, 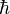 — постоянная Планка,
— постоянная Планка,  — скорость света в вакууме. На уровне ядерных реакций по «силе» электромагнетизм занимает промежуточное положение между сильным и слабым взаимодействиями. Характерные времена распадов, вызванных электромагнитным взаимодействием, — около 10−12 — 10−20 с, в то время, как для сильного взаимодействия — порядка 10−23 с, а для слабого — 103 — 10−13 с. В качестве примера можно привести сравнение сечения рассеяния на протоне фотона с энергией 1 ГэВ и пиона с соответствующей полной энергией в системе центра масс. Для пиона, взаимодействие которого с протоном обусловлено сильным взаимодействием, сечение в 10 000 раз больше[5].
— скорость света в вакууме. На уровне ядерных реакций по «силе» электромагнетизм занимает промежуточное положение между сильным и слабым взаимодействиями. Характерные времена распадов, вызванных электромагнитным взаимодействием, — около 10−12 — 10−20 с, в то время, как для сильного взаимодействия — порядка 10−23 с, а для слабого — 103 — 10−13 с. В качестве примера можно привести сравнение сечения рассеяния на протоне фотона с энергией 1 ГэВ и пиона с соответствующей полной энергией в системе центра масс. Для пиона, взаимодействие которого с протоном обусловлено сильным взаимодействием, сечение в 10 000 раз больше[5].
Электромагнитное взаимодействие сохраняет пространственную чётность (так называемую Р-чётность), зарядовую чётность (так называемую C-чётность), а также такиеквантовые числа, как странность, очарование, красота. Это отличает электромагнетизм от слабого взаимодействия. Одновременно, в отличие от сильного взаимодействия, электромагнитное взаимодействие в процессах с адронами не сохраняет изотопический спин (сопровождаясь испусканием фотона, он может меняться на ±1 или 0) и нарушает G-чётность[5].
Наличие законов сохранения с учётом свойств фотонов накладывает определённые правила отбора на процессы с участием электромагнитного взаимодействия. Например, поскольку спин фотона равен 1, запрещены излучательные переходы между состояниями с нулевым моментом импульса. Необходимость сохранять зарядовую чётность приводит к тому, что системы с положительной зарядовой чётностью распадаются с испусканием только чётного количества фотонов, а с отрицательной зарядовой чётностью — только нечётного. В частности, парапозитроний распадается на два фотона, а ортопозитроний — на три (см. позитроний)[5].
Роль в природе[править | править вики-текст]
За счёт дальнодействия электромагнитное взаимодействие заметно проявляется как на макроскопическом, так и на микроскопическом уровнях. Фактически, подавляющее большинство физических сил в классической механике — силы упругости, силы трения, силы поверхностного натяжения и т. д. — имеют электромагнитную природу[5].
Электромагнитное взаимодействие определяет большинство физических свойств макроскопических тел и, в частности, изменение этих свойств при переходе из одногоагрегатного состояния в другое. Электромагнитное взаимодействие лежит в основе химических превращений. Электрические, магнитные и оптические явления также сводятся к электромагнитному взаимодействию[5].
На микроскопическом уровне электромагнитное взаимодействие (с учётом квантовых эффектов) определяет структуру электронных оболочек атомов, структурумолекул, а также более крупных молекулярных комплексов и кластеров. В частности, величина элементарного электрического заряда определяет размеры атомов и длину связей в молекулах. Например, радиус Бора равен 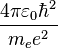 , где
, где 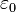 — электрическая постоянная,
— электрическая постоянная, 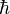 — постоянная Планка,
— постоянная Планка, 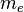 — масса электрона,
— масса электрона,  — элементарный электрический заряд[5].
— элементарный электрический заряд[5].
Теоретическое описание[править | править вики-текст]
Классическая электродинамика[править | править вики-текст]
Основная статья: Классическая электродинамика
В большинстве случаев макроскопические электромагнитные процессы с необходимой степенью точности могут быть описаны в рамках классической электродинамики. В этом случае взаимодействующие объекты рассматриваются как совокупность материальных точек, характеризуемых помимо массы также и электрическим зарядом. При этом полагается, что взаимодействие осуществляется посредством электромагнитного поля — отдельным видом материи, пронизывающим всё пространство.
Электростатика[править | править вики-текст]
Основная статья: Электростатика
Электростатика рассматривает взаимодействие неподвижных заряженных тел. Основным законом электростатики является закон Кулона, устанавливающий связь между силой притяжения/отталкивания двух заряженных материальных точек, величиной их заряда и расстоянием между ними. В математической форме закон Кулона имеет вид[6]:
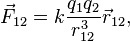
где 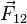 — сила, с которой частица 1 действует на частицу 2,
— сила, с которой частица 1 действует на частицу 2, 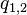 — величины зарядов частиц 1 и 2 соответственно,
— величины зарядов частиц 1 и 2 соответственно, 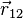 — радиус-вектор, проведённый из точки расположения частицы 1 в точку расположения частицы 2 (
— радиус-вектор, проведённый из точки расположения частицы 1 в точку расположения частицы 2 ( 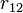 — модуль этого вектора),
— модуль этого вектора), 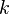 — размерный коэффициент, значение которого зависит от используемойсистемы единиц, в СГС он равен 1, в СИ:
— размерный коэффициент, значение которого зависит от используемойсистемы единиц, в СГС он равен 1, в СИ:
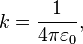
где 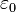 — электрическая постоянная.
— электрическая постоянная.
В рамках электростатики величина электрического поля, создаваемого точечным зарядом, определяется выражением[6]:
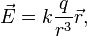
где 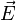 — напряжённость электрического поля в данной точке,
— напряжённость электрического поля в данной точке, 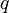 — величина заряда частицы, создающей это поле,
— величина заряда частицы, создающей это поле, 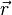 — радиус-вектор, проведённый из точки расположения частицы в точку, где определяется поле (
— радиус-вектор, проведённый из точки расположения частицы в точку, где определяется поле (  — модуль этого вектора).
— модуль этого вектора).
Сила, действующая на заряженную частицу, помещённую в электрическое поле, определяется выражением:
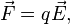
где 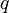 — величина электрического заряда частицы,
— величина электрического заряда частицы, 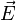 — векторная сумма напряжённостей электрических полей, созданных всеми частицами (за исключением рассматриваемой) в точке, где находится частица[6].
— векторная сумма напряжённостей электрических полей, созданных всеми частицами (за исключением рассматриваемой) в точке, где находится частица[6].
В случае, если заряд распределён в некотором объёме с плотностью 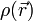 , то электростатическое поле, создаваемое им, может быть найдено из электростатической теоремы Гаусса, имеющей в дифференциальной форме в системе СГС следующий вид[7]:
, то электростатическое поле, создаваемое им, может быть найдено из электростатической теоремы Гаусса, имеющей в дифференциальной форме в системе СГС следующий вид[7]:
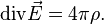
В присутствии поляризуемой диэлектрической среды величина электрического поля, создаваемого свободными зарядами, изменяется из-за влияния связанных зарядов, входящих в состав среды. Это изменение во многих случаях может быть охарактеризовано посредством введения вектора поляризации среды 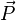 и вектора электрической индукции
и вектора электрической индукции 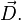 При этом выполняется следующее соотношение[8]:
При этом выполняется следующее соотношение[8]:
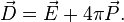
Теорема Гаусса в этом случае записывается в виде[8]:
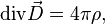
где под 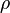 понимается плотность только свободных зарядов.
понимается плотность только свободных зарядов.
В большинстве случаев рассматриваемые поля значительно слабее внутриатомных полей, поэтому справедлива линейная связь между вектором поляризации и напряжённостью электрического поля в данной точке. Для изотропных сред математически этот факт выражается следующим равенством[9]:
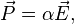
где 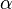 — коэффициент, характеризующий поляризуемость данного диэлектрика при данных температуре и давлении. Аналогично, справедлива линейная связь между напряжённостью и индукцией[9]:
— коэффициент, характеризующий поляризуемость данного диэлектрика при данных температуре и давлении. Аналогично, справедлива линейная связь между напряжённостью и индукцией[9]:
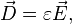
где коэффициент 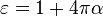 носит название диэлектрической проницаемости[9].
носит название диэлектрической проницаемости[9].
С учётом поляризуемой среды приведённые выше формулы для силы электростатического взаимодействия и напряжённости электростатического поля принимают вид[10]:
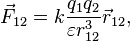
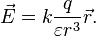
Магнитостатика[править | править вики-текст]
Основная статья: Магнитостатика
Магнитостатика изучает взаимодействие постоянных по величине и неподвижных в пространстве электрических токов, представляющих по своей сути поток заряженных частиц. В основе магнитостатики лежат закон Био — Савара — Лапласа и закон Ампера. Закон Био — Савара — Лапласа позволяет находить величину магнитного поля, создаваемого малым элементом тока. Если имеется линейный элемент тока длиною 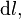 сила тока в котором равна
сила тока в котором равна 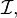 то он создаёт в окружающем пространстве магнитное поле, индукция которого определяется выражением[11]:
то он создаёт в окружающем пространстве магнитное поле, индукция которого определяется выражением[11]:
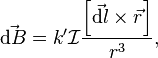
где 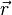 — радиус-вектор, проведённый от точки расположения элемента тока до точки пространства, в которой определяется магнитное поле (
— радиус-вектор, проведённый от точки расположения элемента тока до точки пространства, в которой определяется магнитное поле (  — модуль этого радиус-вектора),
— модуль этого радиус-вектора), 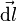 — вектор, длина которого равна
— вектор, длина которого равна 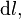 а направление совпадает с направлением тока
а направление совпадает с направлением тока 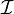 (считая, что направление тока определяется движением положительно заряженных частиц),
(считая, что направление тока определяется движением положительно заряженных частиц), 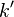 — константа, зависящая от выбора системы единиц: в системе СИ
— константа, зависящая от выбора системы единиц: в системе СИ 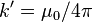 (
( 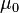 — магнитная постоянная), в системе СГС
— магнитная постоянная), в системе СГС 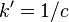 (
(  — скорость света в вакууме). Знаком × в квадратных скобках здесь и ниже обозначается векторное произведение.
— скорость света в вакууме). Знаком × в квадратных скобках здесь и ниже обозначается векторное произведение.
Закон Ампера определяет величину силы, с которой магнитное поле в данной точке действует на элемент тока[12]:
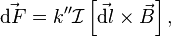
где 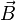 — величина магнитного поля в данной точке, равная векторной сумме магнитных полей, создаваемых всеми другими токами,
— величина магнитного поля в данной точке, равная векторной сумме магнитных полей, создаваемых всеми другими токами, 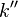 — коэффициент, зависящий от выбранной системы единиц: в системе СИ он равен единице, в системе СГС —
— коэффициент, зависящий от выбранной системы единиц: в системе СИ он равен единице, в системе СГС — 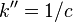 (
(  — скорость света в вакууме).
— скорость света в вакууме).
Закон Ампера является прямым следствием выражения для магнитной составляющей силы Лоренца — силы, с которой электромагнитное поле действует на заряженную частицу[13]:
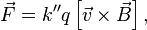
где 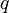 — заряд частицы,
— заряд частицы, 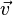 — её скорость.
— её скорость.
Закон Био — Савара — Лапласа может быть переписан в виде для плотности тока 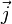 [14]:
[14]:
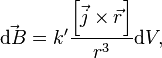
где 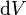 — объём элемента объёмного тока, создающего поле. Из этой формы закона Био — Савара — Лапласа можно вывести теорему о циркуляции магнитной индукции, которая в дифференциальной форме принимает вид[15]:
— объём элемента объёмного тока, создающего поле. Из этой формы закона Био — Савара — Лапласа можно вывести теорему о циркуляции магнитной индукции, которая в дифференциальной форме принимает вид[15]:
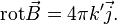
В присутствии магнитной среды (то есть среды, способной к намагничиванию) её влияние характеризуется векторами намагниченности среды 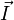 и напряжённости магнитного поля
и напряжённости магнитного поля 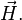 При этом справедлива связь:
При этом справедлива связь:
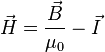 — в системе СИ[16],
— в системе СИ[16],
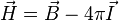 — в системе СГС[17].
— в системе СГС[17].
В линейных изотропных средах справедлива простая связь между величиной намагниченности и приложенным магнитным полем (физически более правильным было бы связывать намагниченность с величиной магнитной индукции, однако по историческим причинам её выражают обычно через напряжённость магнитного поля — ввиду линейной связи между величинами 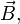
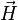 и
и 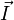 принципиального значения это не имеет)[18][19]:
принципиального значения это не имеет)[18][19]:
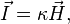
где коэффициент 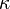 называется магнитной восприимчивостью среды. Часто оперируют также величиной магнитной проницаемости
называется магнитной восприимчивостью среды. Часто оперируют также величиной магнитной проницаемости 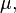 определяемой как:
определяемой как:
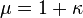 — в системе СИ[19],
— в системе СИ[19],
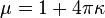 — в системе СГС[18].
— в системе СГС[18].
В этом случае справедливы соотношения:
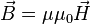 — в системе СИ[19],
— в системе СИ[19],
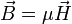 — в системе СГС[18].
— в системе СГС[18].
Следует отметить, что ферромагнетики являются принципиально нелинейными средами, в частности, они подвержены явлению гистерезиса, и поэтому простые соотношения, указанные выше, для них несправедливы.
Теорема о циркуляции в магнитных средах принимает следующий вид[17]:
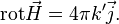
Дата добавления: 2016-01-29; просмотров: 2396;
