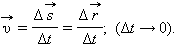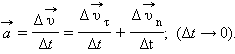Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.
Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути.
В случае достаточно малого промежутка времени Δt пройденный телом путь Δl почти совпадает с модулем вектора перемещения 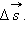 При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).
При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).
|
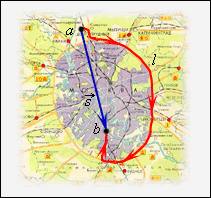
Рисунок 1.1.2.
Пройденный путь l и векторперемещения 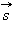 при криволинейномдвижении тела. a и b – начальная и конечная точки пути при криволинейномдвижении тела. a и b – начальная и конечная точки пути
|
Для характеристики движения вводится понятие средней скорости:
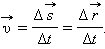
|
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость на бесконечно малом промежутке времени Δt:
|
В математике такой предел называют производной и обозначают 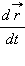 или
или 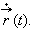
Мгновенная скорость 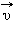 тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.
тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.
|
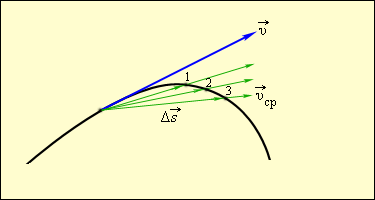
Рисунок 1.1.3.
Средняя и мгновенная скорости. 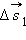 , , 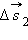 , , 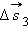 – перемещения за времена – перемещения за времена 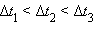 соответственно. Приt → 0 соответственно. Приt → 0 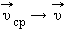
|
При движении тела по криволинейной траектории его скорость 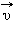 изменяется по модулю и направлению. Изменение вектора скорости
изменяется по модулю и направлению. Изменение вектора скорости 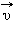 за некоторый малый промежуток времени Δt можно задать с помощью вектора
за некоторый малый промежуток времени Δt можно задать с помощью вектора 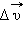 (рис. 1.1.4).
(рис. 1.1.4).
Вектор изменения скорости 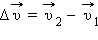 за малое время Δt можно разложить на две составляющие:
за малое время Δt можно разложить на две составляющие:  направленную вдоль вектора
направленную вдоль вектора 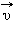 (касательная составляющая), и
(касательная составляющая), и 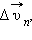 направленную перпендикулярно вектору
направленную перпендикулярно вектору 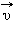 (нормальная составляющая).
(нормальная составляющая).

|
Рисунок 1.1.4.
Изменение вектора скорости по величине и направлению. 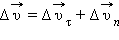 – изменение вектора скорости за время – изменение вектора скорости за время 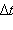
|
Мгновенным ускорением (или просто ускорением) 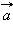 тела называют предел отношения малого изменения скорости
тела называют предел отношения малого изменения скорости 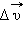 к малому промежутку времени Δt, в течение которого происходило изменение скорости:
к малому промежутку времени Δt, в течение которого происходило изменение скорости:
|
Направление вектора ускорения 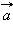 в случае криволинейного движения не совпадает с направлением вектора скорости
в случае криволинейного движения не совпадает с направлением вектора скорости 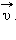 Составляющие вектора ускорения
Составляющие вектора ускорения 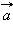 называюткасательным (тангенциальным)
называюткасательным (тангенциальным) 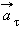 и нормальным
и нормальным 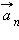 ускорениями (рис. 1.1.5).
ускорениями (рис. 1.1.5).
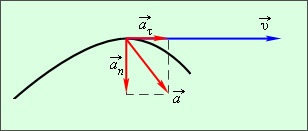
|
| Рисунок 1.1.5. Касательное и нормальное ускорения |
Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю:
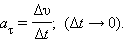
|
Вектор 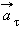 направлен по касательной к траектории.
направлен по касательной к траектории.
Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению.
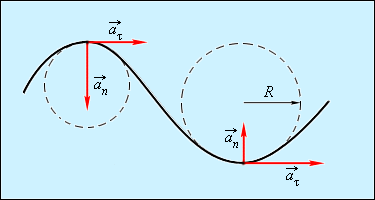
Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).
|
| Рисунок 1.1.6. Движение по дугам окружностей |
Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент:
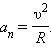
|
Вектор 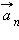 всегда направлен к центру окружности (см. §1.6).
всегда направлен к центру окружности (см. §1.6).
Из рис. 1.1.5 видно, что модуль полного ускорения равен
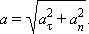
|
Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение 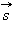 , скорость
, скорость 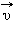 и ускорение
и ускорение 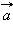 . Путь lявляется скалярной величиной. Перемещение
. Путь lявляется скалярной величиной. Перемещение 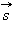 , скорость
, скорость 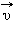 и ускорение
и ускорение 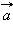 – величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.
– величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.
Дата добавления: 2016-01-29; просмотров: 1448;