Проверка правильности рассуждений
Рассуждение есть утверждение того, что некоторое высказывание (заключение) следует из других высказываний (посылок). Рассуждение считается правильным только в том случае, если из конъюнкции посылок следует заключение, т. е. между конъюнкцией посылок и заключением установлено отношение следствия. Если P1, P2, ... , Pn - посылки, а Q - заключение, то рассуждение правильно, если между высказыванием P1 Ù P2 Ù ... Ù Pn и Q установлено отношение следствия. В этом случае импликация P1 Ù P2 Ù ... Ù Pn®Q должна быть тождественно истинным высказыванием (тавтологией).
Правильность рассуждения можно установить, построив истинностную таблицу высказывания S= P1ÙP2Ù...ÙPn®Q и убедившись в том, что оно тождественно истинно.
При большом числе посылок установить тот факт, что является тавтологией, удобнее с помощью преобразований высказывания к равносильной ему формуле, являющейся тавтологией.
Метод “от противного” заключается в предположении, что заключение ложно, и установление того факта, что при этом конъюнкция P1 Ù P2 Ù ... Ù Pn - ложна (что имеет место в том случае, если хотя бы одна из посылок Pi (  ) принимает значение “ложно”). Если это выполняется, то рассуждение верно, в противном случае - нет. Таким образом, в случае правильного рассуждения мы убеждаемся в том, что импликация S= P1 Ù P2 Ù ... Ù Pn®Qº1, т. к. отсутствует логическая возможность, соответствующая P= P1 Ù P2 Ù ... Ù Pn=1, Q=0, где импликация P®Q принимает значение ложно.
) принимает значение “ложно”). Если это выполняется, то рассуждение верно, в противном случае - нет. Таким образом, в случае правильного рассуждения мы убеждаемся в том, что импликация S= P1 Ù P2 Ù ... Ù Pn®Qº1, т. к. отсутствует логическая возможность, соответствующая P= P1 Ù P2 Ù ... Ù Pn=1, Q=0, где импликация P®Q принимает значение ложно.
Упражнение 2
“Если функция непрерывна на данном интервале и имеет разные знаки на его концах, то внутри интервала функция обращается в нуль. Функция не обращается в нуль внутри данного интервала. но на концах интервала имеет разные знаки. Следовательно, функция разрывна”.
Посылки и заключения в данном рассуждении состоят их следующих элементарных высказываний:
A - “функция непрерывна на данном интервале”,
B - “функция имеет разные знаки на концах интервала”
C - “функция обращается в нуль внутри данного интервала”.
Используя эти обозначения, запишем посылки и заключение в виде формул:
AÙB®C (1-я посылка P1)
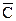 ÙB (2-я посылка P2)
ÙB (2-я посылка P2)

 (заключение Q)
(заключение Q)
Если импликация (AÙB®C)Ù( 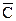 ÙB)®
ÙB)®  =P®Q тождественно истинна, то рассуждение верно. Для проверки правильности рассуждения строим истинностную таблицу:
=P®Q тождественно истинна, то рассуждение верно. Для проверки правильности рассуждения строим истинностную таблицу:
| А | В | С | АВ | АВ®С | 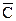
| 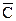 B B
| P1ÙP2 | 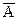
| P1ÙP2®Q |
Убеждаемся, что рассуждение верно. Проведем проверку правильности этого рассуждения методом от противного. Предположим, что заключение Q ложно. Покажем, что в этом случае конъюнкция посылок P1ÙP2 ложна, т. е. P →Q тождественно истинна.
В самом деле, если Q= 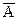 ложно, то A истинно. Пусть P2=
ложно, то A истинно. Пусть P2= 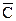 B истина, тогда B - истинно,
B истина, тогда B - истинно, 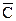 - истинно т. е. C - ложно, но в этом случае посылка принимает значение ложно, так как P1=АВ®С принимает значение ложно, так как AB=1, а С=0, что и требовалось проверить.
- истинно т. е. C - ложно, но в этом случае посылка принимает значение ложно, так как P1=АВ®С принимает значение ложно, так как AB=1, а С=0, что и требовалось проверить.
Правильность данного рассуждения можно проверить, преобразовав формулу P1ÙP2 к некоторой равносильной ей формуле, которая задает заведомо тождественно истинное высказывание.
Дата добавления: 2016-01-26; просмотров: 1292;
