Теория размерностей

Теория размерностей используется в том случае, когда нет дифференциального уравнения, описывающего данный процесс. В условиях вынужденной конвекции величина коэффициента теплоотдачи является функцией по крайней мере шести независимых переменных: весовой скорости u, кг/(м²×с); линейного размера l; вязкости m, кг/(м×с); теплоемкости С, Дж/(кг×К); плотности r, кг/м³ и теплопроводности l, Вт/(м×К).

При экспериментальном определении a Вт/(м²×К) необходимо исследовать зависисмость a от шести переменных и провести число опытов 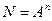, где А — число опытов с одной переменной, например, А = 10; n — число независимых переменных. Для данного примера оказывается, что число опытов равно одному миллиону, что является совершенно нереальным. Применение же теории размерностей приводит к сокращению независимых переменных. В условиях вынужденной конвекции коэффициент теплоотдачи является функцией

a = a(u, l, m, С, r, l). (4.42)

Полный дифференциал a равен:

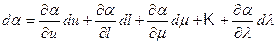. (4.43)

Для перехода к безразмерным (относительным) величинам необходимо иметь переменные, не отсчитываемые от постоянного «нулевого» уровня. Разделим полученное уравнение на a и одновременно делим и умножаем каждое слагаемое на соответствующие значения (l/l; u/u; m/m и т. д.), тогда

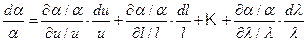. (4.44)

Считаем, что соотношения частных производных являются постоянными:

; ; …; ,

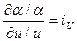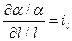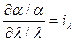тогда получим

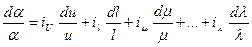. (4.45)

Интегрируем полученное выражение:

ln a=i_u ln u+i_l ln l+…+i_l ln l+ln C₀. (4.46)

Потенцируем и получим

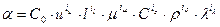. (4.47)

Необходимым условием общности полученного решения должно быть требование безразмерности постоянной С₀ или ее обратной величины:

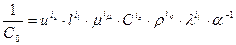. (4.48)

Это уравнение не зависит от системы единиц, а в связи с тем, что С₀ является безразмерной, то все единицы измерений (справа) должны входить в это уравнение в «0» степени. Для исключения размерностей составим табл. 2.1.

Таблица 4.1