Операционный усилитель 2 страница
13) Закон поглощения:
а) х + ху = х;
б) х (х +у) = х.
14) Закон склеивания:
а) ху + 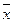 у = у;
у = у;
б) (х + у) ( 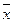 + у) = у.
+ у) = у.
Здесь в результате операции исчезает переменная, входящая непосредственно и с отрицанием. Слагаемые, которые отличаются только одной переменной, причем в одном из них переменная имеет отрицание, в другом – нет, называются соседними, например, ху и 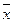 у – соседние слагаемые.
у – соседние слагаемые.
15) Теоремы де Моргана или законы отрицания:
а) 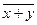 =
= 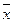 ·
· 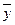 ;
;
б) 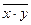 =
= 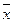 +
+ 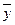 .
.
Теоремы де Моргана справедливы для любого числа переменных:
в) 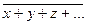 =
= 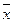 ·
· 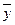 ·
· 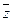 · … ;
· … ;
г) 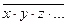 =
= 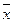 +
+ 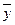 +
+ 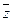 + … .
+ … .
При переходе к элементному базису И-НЕ и ИЛИ-НЕ теоремы де Моргана используются в виде:
х + у = 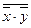 ;
;
х · у = 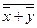 .
.
Именно в таком варианте их и следует запоминать.
Рассмотренные правила булевой алгебры необходимы для анализа и синтеза логических схем. Правила 9–15 имеют большое значение для преобразования логических выражений с целью упрощения и построения логических схем в заданном элементном базисе.
Способы представления булевых функций
Результат выполнения логических операций над двоичными переменными принято называть булевой функцией.
Задать булеву функцию – это значит указать значения функции (0 или 1) при всех возможных комбинациях значений аргументов. Каждую конкретную комбинацию значений аргументов называют набором или точкой.
Например, набор трех переменных А, В и С задан значениями аргументов 101. Двоичное число, представляющее набор, называется номером набора. В нашем примере имеем пятый набор, так как 101 – это двоичное число 5. А всего у функций 3-х переменных 23 наборов, то есть восемь. При n аргументах существует 2n наборов.
Если функция определена на всех наборах, то она является полностью определенной. Если же на некоторых наборах значение функции не задано, функция называется частично определенной (недоопределенной). В реальных схемах это имеет место в случае, когда известно, что некоторые комбинации входных переменных невозможны. Тогда значения функции на соответствующих наборах не задаются, а сами наборы называются запрещенными. При этом возникают так называемые факультативные(необязательные) условия для функции. Значения функции на запрещенных наборах можно установить по своему усмотрению, то есть частично определенную функцию можно доопределить.
Одной из задач проектирования цифровых устройств можно считать получение логических функций в удобном для реализации виде. В зависимости от того, как заданы первоначальные сведения о работе проектируемого устройства (в виде словесного описания, в форме таблицы) существуют несколько способов представления функции, задающей работу устройства.
Словесный способ задания функции. Словесное описание функции, реализуемой проектируемым устройством, должно однозначно определять все случаи, в которых выходные сигналы принимают значения 1 или 0. Примером правильного описания может служить следующее задание: «Спроектировать устройство с тремя входами А, В и С, на выходе которого появляется сигнал F = 1 в случае, если на любые два или на все три входа подан сигнал 1».
Это означает, что функция равна единице, если любые два аргумента или все три равны 1. Во всех остальных случаях функция равна 0. Этим функция и логика работы соответствующего устройства полностью заданы.
Табличный способ задания функции. Таблица значений функции (таблица истинности) – это перечисление всех возможных комбинаций входных сигналов и соответствующих им значений выходных сигналов. Для устройства, заданного приведенным выше словесным описанием, таблица значений функции имеет вид как на рис. 32, а. Данная функция описывает мажоритарный элемент– логический элемент, имеющий всегда нечетное число входов и один выход, состояние которого определяется состоянием большинства входов. Условное графическое обозначение этого логического элемента показано на рис.32, б.
| Входы | Выход | ||||
| Номер набора | А | В | С | F | 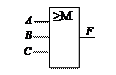
|
| а | б | ||||
| Рис. 32. Мажоритарный элемент: а – таблица работы; б – условное графическое обозначение |
Таблица истинности является более конкретным и полным представлением функции, чем словесное описание, и поэтому чаще всего от словесного описания переходят к таблице.
Алгебраический способ задания функции. От таблицы можно перейти к аналитической форме функции или к структурной формуле. В такой форме удобно производить различные преобразования функций, например, с целью минимизации. Существуют две формы функции в алгебраическом виде, называемые нормальными.
Первая форма, которая также называется дизъюнктивной нормальной формой (ДНФ), представляет собой сумму элементарных произведений, в каждое из которых аргумент или его отрицание входит не более одного раза, например:
F(А,В,С) = А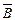 + В С +
+ В С + 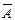
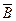 С.
С.
Если каждое слагаемое содержит все переменные или их отрицания, имеем первую стандартную форму, или совершенную дизъюнктивную нормальную форму (СДНФ), например:
F(А,В,С) = А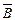 С +
С + 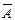 В
В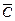 + А В
+ А В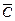 +
+ 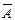
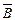 С.
С.
Вторая форма или конъюнктивная нормальная форма (КНФ)есть логическое произведение элементарных логических сумм. Когда каждая сумма содержит все переменные или их отрицания, имеем вторую стандартную, или совершенную конъюнктивную нормальную форму (СКНФ), например:
F(А,В,С) = (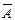 +В+
+В+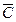 ) (А+
) (А+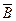 +С) (
+С) (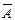 +
+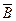 +С).
+С).
Переход от таблицы к первой стандартной форме осуществляется следующим образом. Для каждого набора (из таблицы истинности), на котором функция равна 1, записывается элементарное произведение всех аргументов, причем если аргумент принимает значение 0, то пишется его отрицание. Затем производится логическое сложение этих элементарных произведений. Для функции мажоритарного элемента получается:
F(А,В,С) = 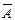 В С + А
В С + А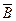 С + А В
С + А В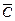 + А В С.
+ А В С.
При переходе ко второй стандартной форме необходимо для каждого набора (из таблицы истинности), на котором функция равна 0, составить элементарную сумму, причем, если аргумент в этом наборе принимает значение 1, то пишется его отрицание. Затем суммы объединяются операцией логического умножения. В нашем примере будем иметь:
F(А,В,С) =(А+В+С)(А+В+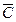 )(А+
)(А+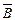 +С) (
+С) (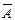 +В+С).
+В+С).
Как видно из рассмотренного примера, структурная формула может быть составлена по единицам и по нулям единственным образом. Из этого следует, что любая функция имеет единственную первую и вторую стандартные формы.
Числовой способ задания функции. Для числового представления функции в первой стандартной форме под знаком суммы перечисляются номера наборов, на которых функция равна 1. При этом подразумевается, что на остальных наборах она равна 0. Для нашего примера:
F(А,В,С) = Σ(3, 5, 6, 7).
Для второй стандартной формы под знаком произведения перечисляют номера наборов, на которых функция равна 0:
F(А,В,С) = Π(0, 1, 2, 4).
Графический способ задания функции (чаще всего временные диаграммы). Временные диаграммы работы устройства приводятся в качестве вспомогательного материала, дополняющего один из предыдущих способов задания функции. Временные диаграммы иллюстрируют прохождение входных и выходных сигналов во времени. На рис. 33 приведены для примера временные диаграммы некоторых простейших функций.

|
| Рис. 33. Временные диаграммы простейших функций |
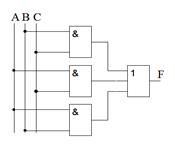
Переход от структурной формулы к логической схеме
На основании полученной структурной формулы можно построить схему, состоящую из элементов ИЛИ, И, НЕ, которая будет обладать заданными логическими свойствами. Иначе говоря, она будет реализовывать заданную булеву функцию.
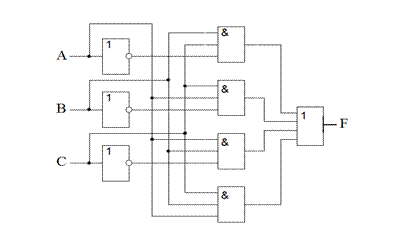
Логические элементы, предназначенные для выполнения указанных в формуле операций, располагаются в схеме, начиная от входов, в таком же порядке, в каком выполняются операции в алгебре Буля. Для заданной ранее функции мажоритарного элемента F(А,В,С) = 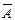 ВС + А
ВС + А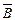 С + АВ
С + АВ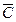 + АВС сначала ставятся инверторы для получения отрицания входных переменных, затем элементы И, а потом элемент ИЛИ. В результате получим схему, содержащую три инвертора, четыре элемента 3И и один элемент 4ИЛИ (рис. 34).
+ АВС сначала ставятся инверторы для получения отрицания входных переменных, затем элементы И, а потом элемент ИЛИ. В результате получим схему, содержащую три инвертора, четыре элемента 3И и один элемент 4ИЛИ (рис. 34).
|
| Рис. 34. Принципиальная схема мажоритарного элемента |
Методы минимизации булевых функций
Переходу к логической схеме всегда должна предшествовать минимизация, то есть упрощение структурных формул с целью приведения их к такому виду, когда количество элементов, необходимых для построения схемы, будет минимальным.
Минимизация с помощью теорем алгебры Буля.
В основу минимизации положены правила и законы булевой алгебры. Чаще всего применяются теоремы склеивания и поглощения. В функции, представленной в первой стандартной форме, отыскиваются соседние слагаемые, и производится их склеивание. После того, как возможности склеивания исчерпаны, делается попытка исключить избыточные слагаемые применением закона поглощения.
В результате получается неизбыточная или так называемая тупиковая форма. Следует заметить, что исключение избыточных слагаемых может быть произведено различными способами, поэтому для одной и той же функции может быть получено несколько тупиковых форм. Выбирается та форма, для реализации которой требуется меньшее число логических элементов.
Для примера рассмотрим упрощение функции, полученной для мажоритарного элемента:
F(А,В,С) = 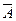 ВС + А
ВС + А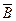 С + АВ
С + АВ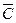 + АВС.
+ АВС.
Добавим еще два слагаемых АВС (от чего значение функции не изменится), а затем произведем возможные склеивания:
F(А,В,С) = 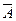 ВС + А
ВС + А 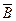 С + АВ
С + АВ 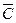 + АВС + АВС +АВС =
+ АВС + АВС +АВС =
= (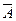 ВС + АВС) + (А
ВС + АВС) + (А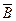 С + АВС) + (АВ
С + АВС) + (АВ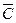 + АВС) =
+ АВС) =
= ВС +АС + АВ.
Таким образом, в функции вместо четырех слагаемых третьего ранга получили 3 слагаемых второго ранга:
F(А,В,С) = ВС +АС + АВ.
Схема, реализующая последнее выражение, приведена на рис. 35.
| Рис. 35. Принципиальная схема мажоритарного элемента (после минимизации) |
Минимизация функций методом карт Карно.
Метод упрощения с помощью теорем алгебры Буля трудоемок, требует большого опыта, интуиции, мало нагляден, и при этом легко может возникнуть ошибка. Он пригоден для преобразований простейших алгебраических выражений. Для упрощения сложных логических функций применяется множество других методов, среди которых наиболее пригоден для технической практики метод минимизации с использованием карт Карно.
Карта Карно представляет собой прямоугольник, разбитый на квадраты, число которых равно общему числу наборов для заданной функции n-переменных, то есть 2n. Для функции трех переменных число квадратов – 8, для четырех переменных – 16, пяти переменных – 32 и т.д. Каждый квадрат соответствует определенному набору, причем эти квадраты располагаются так, чтобы соседние слагаемые соответствовали соседним квадратам. Это значительно облегчает процедуру склеивания (рис. 36, а). Символу 0 в карте Карно соответствует отрицание переменной, например, 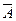 , а символу 1 – сама переменная, например А. Символы 0 и 1 в карте а специально проставлены так, чтобы соседние квадраты отличались бы значениями только одной переменной.
, а символу 1 – сама переменная, например А. Символы 0 и 1 в карте а специально проставлены так, чтобы соседние квадраты отличались бы значениями только одной переменной.
Чтобы выполнить минимизацию, функцию в первой стандартной форме (ДНФ) наносят на карту, отмечая знаком 1 квадраты, соответствующие тем наборам, на которых функция равна 1. Остальные наборы отмечают знаком 0, либо вообще оставляют без отметки (рис. 36, б). Таким образом, карта Карно – это еще один способ представления булевых функций.
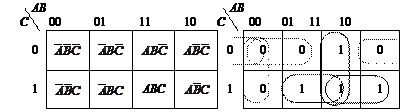
| |
| а | б |
| Рис. 36. Карта Карно для трех переменных А, В, С (а) и для функции мажоритарного элемента (б) |
Заполним карты Карно для уже знакомой мажоритарной функции. Функция содержит три переменных, следовательно, число квадратов в карте восемь, так как 23 = 8. Из таблицы истинности запишем единицы в те квадраты карты Карно, которые соответствуют наборам, на которых функция равна 1 (см. рис. 36,б). Затем произведем объединение единиц в контуры. Объединять можно 2, 4, 8 и 16 квадратов, то есть 2n. Это равносильно объединению соседних слагаемых в алгебраическом методе минимизации. Одни и те же квадраты могут входить несколько раз в разные контуры.
Объединение в контур двух соседних квадратов исключает одну переменную, объединение четырех соседних квадратов исключает четыре переменные и так далее. Возможно также объединение крайних квадратов на противоположных сторонах карты. Число контуров определяет число слагаемых в конечном алгебраическом выражении.
В каждом слагаемом записываются только те переменные, которые являются общими для данного контура. В результате минимизации функции мажоритарного элемента по единицам получается выражение
F(А,В,С) = ВС + АС + АВ,
то есть то же самое выражение, что и с использованием теоремы склеивания алгебры Буля.
В процедуре минимизации работают следующие правила:
– чем больше квадратов входит в контур, тем лучше эффект минимизации (исключается большее число аргументов);
– чем меньше получено контуров, тем меньше слагаемых будет в минимизированном выражении, тем проще получится схема.
Объединять в карте Карно можно не только единицы, но и нули, если функция n-переменных представлена в полной стандартной форме, то есть содержит все 2n слагаемых. При этом если в виде первой стандартной формы функция содержит m слагаемых, то ее отрицание 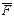 должно содержать остальные (2n – m) слагаемых. Для любой двоичной переменной F+
должно содержать остальные (2n – m) слагаемых. Для любой двоичной переменной F+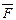 = 1. Таким образом, при объединении нулей в карте Карно, получают отрицание функции. Используя пунктирные контуры на рис. 36, б для мажоритарной функции, получим:
= 1. Таким образом, при объединении нулей в карте Карно, получают отрицание функции. Используя пунктирные контуры на рис. 36, б для мажоритарной функции, получим:
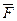 (А,В,С) =
(А,В,С) = 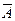
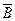 +
+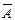
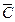 +
+ 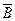
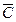 .
.
Для функций четырех переменных карты Карно будут состоять из 24, то есть из 16 квадратов. В квадратах, соответствующих наборам, на которых функция не определена, ставится знак «Ø» (факультативный набор). Недоопределенные (запрещенные) комбинации при работе проектируемой схемы не будут встречаться, поэтому на запрещенных наборах функцию можно произвольно доопределить, установив ее значения (0 или 1) по своему усмотрению, причем доопределяют функцию только в тех квадратах, которые входят в контур, что облегчает процедуру склеивания (рис. 37).
  
| ||
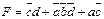 , ,
| 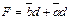 , ,
| 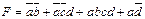 , ,
|
| Рис. 37. Минимизация функций четырех переменных методом карт Карно |
Комбинационные интегральные схемы
Любое цифровое устройство состоит из элементов двух типов: логических и элементов памяти, служащих для хранения информации. Если схема не содержит элементов памяти, ее называют комбинационной.
Комбинационные интегральные схемы выполняют более сложные функции, чем логические элементы. Их выводы объединены в функциональные группы и не являются полностью взаимозаменяемыми, как у логических элементов, у которых любые два входа можно поменять местами и при этом выходной сигнал не изменится. У комбинационных интегральных схем такое сделать невозможно, поскольку у каждого входа имеется свое назначение.
Состав набора интегральных микросхем, входящих в стандартные серии, был определен, исходя из наиболее часто встречающихся задач. К комбинационным интегральным схемам относятся шифраторы, дешифраторы, преобразователи кодов, сумматоры, коммутаторы и другие устройства.
Шифраторы
Шифратор преобразует сигнал, поданный на один из m входов в выходной параллельный двоичный код, соответствующий номеру возбужденного входа. Число входов и выходов шифратора связано соотношением m = 2n, где m – число входов, а n – число выходов. Часто связь между входами и выходами записывается как 8×3, 16×4, 32×5 и т.д. Для десятичной системы счисления используются шифраторы 10×4, то есть шифраторы с неполным числом входов.
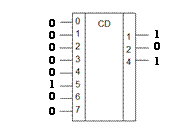
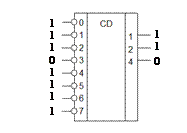
Часто шифраторы используются для формирования кода номера нажатой кнопки или положения многопозиционного переключателя. Выделить выбранный вход можно логической единицей (1) или логическим нулем (0), соответственно различают шифраторы с прямыми входами (активный входной уровень – лог. 1) и с и инверсными входами (активный входной уровень – лог. 0). На условном графическом обозначении шифратора ставятся буквы CD от английского coder – кодер, шифратор (рис. 39).
| 
|
| а | б |
| Рис. 39. Условное графическое обозначение шифраторов 8×3: а – с прямыми входами (активный 5-й вход); б – с инверсными входами (активный 3-й вход) |
На рис. 40, а приведена таблица работы десятичного шифратора с прямыми входами, а на рис. 40, б показано его условное графическое обозначение.
| № | Код «1 из 10» (унитарный) | Код 8-4-2-1 | 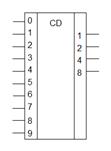
| |||||||||||
| х0 | х1 | х2 | х3 | х4 | х5 | х6 | х7 | х8 | х9 | y4 | y3 | y2 | y1 | |
| а | б | |||||||||||||
| Рис. 40. Шифратор 10×4: а – таблица истинности; б – условное графическое обозначение |
В обозначениях интегральных шифраторов присутствуют буквы ИВ. Например, КМ555ИВ1, К555ИВ3.
Дешифраторы
Дешифратором, или декодером (decoder – англ., в графическом обозначении – DC), называют устройство, преобразующее двоичный код в унитарный (код «1 из m»). Из всех выходов дешифратора активный уровень имеется только на одном, номер которого равен поданному на входы двоичному числу. Дешифратор поэтому еще называют устройством для распознавания кодовых комбинаций.
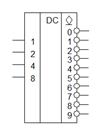
Дешифратор выполняет функцию, обратную той, что выполняет шифратор, поэтому имеет похожую таблицу истинности (рис.41, а), но в ней входы и выходы следует поменять местами. Если дешифратор имеет n входов и m выходов и использует все возможные наборы переменных, то m = 2n. Такой дешифратор называется полным. Примером полных дешифраторов являются дешифраторы 3×8, 4×16, 5×32 и т.д. Из неполных дешифраторов наибольшее распространение получили дешифраторы 4×10 для распознавания двоично-десятичных кодов. На рис. 42, а и б приведены дешифраторы 4×10 в составе серий интегральных микросхем. Как видно, дешифраторы могут иметь как прямые, так и инверсные выходы.
В обозначениях микросхем дешифраторов присутствуют буквы ИД. Например, 133ИД1, 155ИД1, 561ИД1.
| 
| 
|
| 133ИД1, 155ИД1, 555ИД1 | 561ИД1, 564ИД1 | К555ИД7 |
| a | б | в |
| Рис.42. Микросхемы дешифраторов 4×10 (а,б), дешифратор К555ИД7 в режиме демультиплексора (в). |
Преобразователи кодов
Дата добавления: 2015-11-28; просмотров: 1180;