Операционный усилитель 1 страница
Операционным усилителем (ОУ) называется аналоговая интегральная схема, которая представляет собой усилитель постоянного тока дифференциального типа, имеющий два входа и один несимметричный выход, и обладающий коэффициентом усиления несколько тысяч в диапазоне частот от нуля до нескольких мегагерц. Название усилителя обусловлено первоначальной областью его применения – выполнением различных операций над аналоговыми сигналами (сложение, вычитание, интегрирование, дифференцирование и др.). В настоящее время операционные усилители выполняют роль многофункциональных узлов при реализации устройств электроники различного назначения. Они применяются для усиления, ограничения, перемножения, частотной фильтрации, генерации, стабилизации сигналов в устройствах непрерывного и импульсного действия.
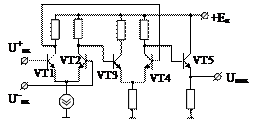
На рис. 21, а представлена упрощенная электрическая схема операционного усилителя, полностью соответствующая данному выше определению ОУ.
В этой схеме входной дифференциальный каскад на транзисторах VT1 и VT2 обеспечивает усиление дифференциального входного сигнала, подавляя синфазный. Он работает в режиме малого сигнала, обеспечивая тем самым очень большое входное сопротивление каскада.
Промежуточный квазидифференциальный каскад на транзисторах VT3 и VT4 не только дополнительно усиливает входной сигнал, но и позволяет осуществить переход от симметричного входа к несимметричному выходу усилителя за счет наличия коллекторного сопротивления только в одном плече каскада.
 а
а
|  б
б
|
| Рис. 21. Операционный усилитель: а – упрощенная электрическая схема; б – условное графическое обозначение |
На транзисторе VT5 построен выходной каскад ОУ, выполненный по схеме эмиттерного повторителя). Он обеспечивает низкое выходное сопротивление ОУ. Для получения необходимого коэффициента усиления ОУ в схему включают два, три и более промежуточных каскадов. Выходной сигнал ОУ снимается с выхода эмиттерного повторителя относительно земли.
Базовый электрод транзистора VT1 является неинвертирующим входом ОУ (не переворачивает фазу входного напряжения), базовый электрод транзистора VT2 является инвертирующим входом ОУ, поскольку сдвигает фазу входного сигнала на 180˚.
Основные параметры и характеристики ОУ
Учитывая внутреннее устройство интегральной микросхемы, называемой операционным усилителем (рис. 21, а), следует считать, что она является высококачественным усилителем и характеризуется параметрами, свойственными идеальному усилителю. К их числу относятся бесконечно большое входное и бесконечно малое выходное сопротивления, бесконечно большой коэффициент усиления и бесконечно большая полоса пропускания,
В реальности идеальных ОУ не существует, но из идеализации ОУ вытекают два замечательных следствия, которые используются при анализе схем, включающих ОУ, а также при выполнении простых инженерных расчетов.
Первое следствие: входная цепь усилителя тока не потребляет.
Второе следстви формулируется двояко: входные зажимы ОУ эквипотенциальны, либо входы ОУ виртуально замкнуты.
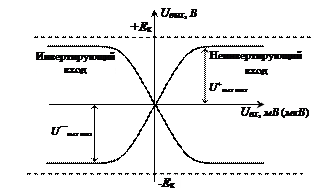
Одной из основных характеристик идеального ОУ является амплитудная,или передаточная характеристика Uвых = f (Uвх). Учитывая наличие инвертирующего и неинвертирующего входов ОУ, её можно представить, как на рис. 22.
Амплитудная характеристика идеального ОУ проходит через ноль, так как ОУ удовлетворяет требованиям, предъявляемым к дифференциальным усилителям: если Uвх = 0, то и Uвых = 0. Такое состояние называют балансом ОУ.
|
| Рис. 22. Амплитудная характеристика ОУ |
Линейному участку характеристик соответствует пропорциональная зависимость выходного напряжения от входного. Угол наклона линейного участка определяется коэффициентом усиления ОУ, который зависит от типа ОУ и может составлять сотни тысяч и более.
Горизонтальные участки характеристик соответствуют утрате транзисторами выходного каскада усилительных свойств и переходу их в режим насыщения или в режим отсечки. Чтобы выходные транзисторы работали не как ключи, а как усилительные приборы, падение напряжения коллектор-эмиттер должно составлять 1–2 В. Таким образом, выходное напряжение ОУ может увеличиваться до (+Ек – 2В) и уменьшаться до (–Ек + 2В). Это напряжение принято обозначать U+вых max и U¯вых max. Таким образом, U+вых max = +Ек – 2В; U¯вых max = –Ек + 2В, иногда его называют напряжением насыщения ОУ.
Схемы на операционных усилителях
Поскольку коэффициент усиления ОУ очень велик, а выходное напряжение не превышает ± Ек (рис. 22.), то ОУ сохраняет свои линейные свойства и способен усиливать входные сигналы не более нескольких единиц – десятков микровольт. Чтобы ОУ мог усиливать реальные входные сигналы, приходится использовать его в схемах с ООС. При этом коэффициент усиления становится гораздо меньше по величине и зависит от параметров цепей обратной связи, но именно это является выгодным фактором при построении схем на операционных усилителях.
Инвертирующий усилитель.
В схеме инвертирующего усилителя (рис. 23) обратная связь создается с помощью резистора Rос с выхода ОУ на его инвертирующий вход, туда же через резистор R1 подается и входной сигнал. Неинвертирующий вход ОУ при этом заземляется.
 

| Воспользовавшись свойства-ми идеального ОУ, можно рассчитать выходное напряжение этой схемы и ее коэффициент усиления. Для этой схемы Uвых = URос , так как один вывод у Rос и Rн – общий, а вторые соединены с корпусом (входные зажимы ОУ эквипотенциальны). Ток, протекающий через Rос, | ||||||||||
| Рис. 23. Схема инвертирующего усилителя |
можно рассчитать по первому закону Кирхгофа для узла: IR1 + Iвх = Iос, но, учитывая, что Iвх = 0 (первое следствие), получаем
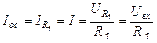 .
.
Таким образом,
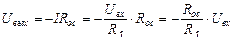 ,
,
а коэффициент усиления схемы определяется как
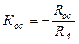 .
.
Знак «минус» в этой формуле объясняется тем, что входной и выходной сигналы находятся в противофазе.
Неинвертирующий усилитель.
В схеме неинвертирующего усилителя (рис. 24) отрицательная обратная связь осуществляется по-прежнему на инвертирующий вход. Источник же входного сигнала включен в цепь неинвертирующего входа, поэтому выходное напряжение будет иметь ту же полярность, что и входное.
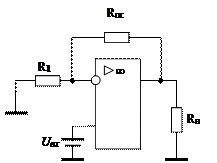
Выходное напряжение в этой схеме определяется суммой напряжений на резисторе Rос и на резисторе R1 :
Uвых = URос + UR1 .
|
| Рис. 24. Схема неинвертирующего усилителя |
Поскольку Uдиф = 0 (второе следствие), то потенциал инвертирующего входа и падение напряжения UR1 будут равны Uвх Тогда выражение для выходного напряжения примет вид:
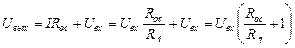 .
.
Коэффициент усиления схемы будет со знаком «плюс»:
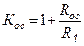 .
.
Компараторы на ОУ.
Рассмотренные ранее схемы с использованием ОУ предполагали работу ОУ в усилительном режиме, то есть на линейном участке амплитудной характеристики. При большом входном сигнале выходное напряжение ОУ ограничено значением ±Uвых mах, что обусловлено ключевым режимом работы транзисторов выходного каскада. При этом значение выходного напряжения зависит от того, какое из входных напряжений больше.
Если U+вх – U¯вх >0 , или U+вх > U¯вх , то Uвых=U+вых mах.
Если U+вх – U¯вх <0 , или U+вх < U¯вх , то Uвых=U¯вых mах .
Таким образом, ОУ является схемой сравнения напряжений, то есть компаратором.
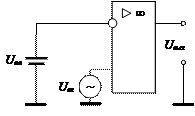
Рассмотрим схему простейшего компаратора и временные диаграммы его работы (рис. 25). Синусоидальное напряжение подано на неинвертирующий вход, а на инвертирующий вход подано опорное напряжение, с которым сравнивается переменный сигнал.
| 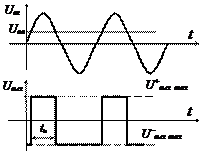
|
| а б Рис. 25. Простейший компаратор на ОУ: а – схема; б – временные диаграммы |
Компаратор переключается в момент равенства напряжений Uвх = Uоп, а выходное напряжение имеет форму прямоугольных импульсов с амплитудой ±Uвых mах. Ширина этих импульсов зависит от величины Uоп при заданной амплитуде входного сигнала. Из этого следует, что простейший компаратор может служить преобразователем синусоидального напряжения в прямоугольное. В этой же схеме осуществляется преобразование напряжения Uвх в длительность импульса tи.
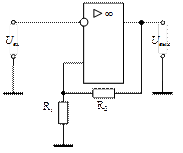
Наряду с простейшей схемой компаратора широкое применение нашла схема компаратора с положительной обратной связью (ПОС), которая осуществляется по неинвертирующему входу с помощью резисторов R1 и R2 (рис. 26, а). Входной сигнал подается на инвертирующий вход.
При значительном отрицательном напряжении на инвертирующем входе ОУ Uвых = U+вых max (рис. 26, б). Переключение схемы в состояние U¯вых max происходит при достижении входным напряжением порога срабатывания Uср=βU+вых max, а возвращение в исходное состояние Uвых = U+вых max – при снижении Uвх до напряжения порога отпускания
Uотп=βUˉвых max, где 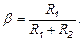
| 
|
| аб Рис. 26. Компаратор с ПОС: а – схема; б – передаточная характеристика |
Схема компаратора с положительной обратной связью (рис. 26, а) служит основой для построения генераторов прямоугольных импульсов на ОУ.
Мультивибраторы на ОУ.
Если схему компаратора, представленного на рис. 26, а дополнить времязадающей RC-цепью, подключенной к инвертирующему входу, то получится схема симметричного мультивибратора – устройства, предназначенного для генерирования последовательности импульсов прямоугольной формы с требуемыми параметрами – амплитудой, длительностью, частотой следования импульсов (рис, а. 27).
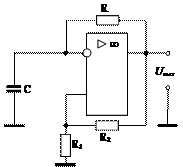
| 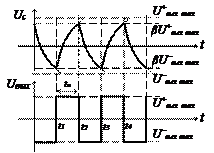
|
| аб Рис. 27. Мультивибратор на ОУ: а – схема; б – осциллограммы |
Процессы заряда-разряда конденсатора в схеме на рис. 27, а формируют переменный сигнал на инвертирующем входе ОУ, а ПОС создает опорное напряжение Uоп=βUвых mах на неинвертирующем входе. Работу схемы поясняют осциллограммы (см. рис. 27, б).
Частота следования импульсов симметричного мультивибратора
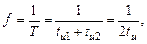
а tu можно определить по длительности интервала tu1 , где конденсатор С перезаряжается от напряжения βU+вых max до напряжения βU−вых max через резистор R. Нетрудно показать, что длительность импульса равна
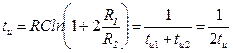 ,
,
и формула для определения частоты имеет вид:
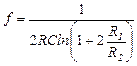 .
.
ЦИФРОВЫЕ УСТРОЙСТВА
Цифровые сигналы
Основой построения любого устройства, использующего цифровую информацию, являются элементы двух типов: логические и запоминающие. Логические элементы выполняют простейшие логические операции над цифровой информацией, а запоминающие служат для ее хранения.
Сигналы на входах и выходах логических элементов являются обычно двоичными (бинарными), то есть принимают лишь два значения, символически обозначаемые «0» и «1». Поэтому их называют также двоичными переменными и обозначают буквами латинского алфавита (например, входные сигналы Х1, Х2, Х3, … Хn, а результат операции, то есть выходной сигнал, F). Следует отметить, что цифры 0 и 1 не дают никакой количественной оценки состояний элементов. Они лишь обозначают эти состояния.
На рис. 28 приведены временные диаграммы однополярных сигналов, у которых логическому нулю и логической единице соответствуют различные уровни напряжения U 0 и U 1.

|
| Рис. 28. Цифровые сигналы для положительной логики при U > 0 (а), U < 0 (б) и для отрицательной логики при U > 0 (в), U < 0 (г) |
Принято считать, что если более высокому уровню присвоено состояние 1, то независимо от полярности напряжения, такой сигнал соответствует положительной логике (см. рис. 28, а, б). Если состояние 1 присвоено более низкому уровню, то такой сигнал соответствует отрицательной логике (см. рис. 28, в, г).
Одиночный цифровой сигнал не слишком информативен, так как он может принимать только два значения: 0 и 1. Поэтому в тех случаях, когда необходимо передавать, обрабатывать или хранить большие объемы информации, обычно применяют несколько параллельных цифровых сигналов. При этом все эти сигналы должны рассматриваться только одновременно, каждый их них по отдельности не имеет смысла. В таких случаях говорят о двоичных кодах, то есть о кодах, образованных цифровыми сигналами. Каждый из сигналов, входящих в код, называется разрядом. Чем больше разрядов входит в код, тем больше значений может принимать данный код.
В отличие от привычного для нас десятичного кодирования чисел, то есть кода с основанием 10, при двоичном кодировании в основании кода лежит число 2 (рис. 29). Каждая цифра кода (каждый разряд) двоичного кода может принимать не десять значений (как в десятичном коде 0, 1, 2, 3, …, 9), а всего лишь два значения – 0 и 1.

Рис. 29. Десятичное и двоичное кодирование информации
В общем виде число в двоичной системе счисления записывается как
A2 = an 2n + an-1 2n-1 + … a1 21 + a0 20.
Здесь коэффициентами аn являются цифры 0 и 1, а основанием – число 2.
В табл. 1 показано соответствие первых двадцати чисел в десятичной и двоичной системах.
Таблица 1. Соответствие чисел в десятичной и двоичной системах
| Десятичная система | Двоичная система | Десятичная система | Двоичная система |
Основные положения теории логических схем
Сложные зависимости между входными и выходными переменными в логических схемах могут быть реализованы различными способами. По этой причине схемы, выполняющие одни и те же функции, могут отличаться по числу входящих в них элементов и по способу их соединения. Проектирование экономически выгодных логических схем осуществляется с помощью булевой алгебры (алгебры Буля) – математического аппарата, значительно облегчающего решение этой задачи.
Основные логические операции и логические элементы
В булевой алгебре над переменными (0 или 1) могут производиться три основных действия: логическое сложение, логическое умножение и логическое отрицание.
Логическое сложение, называемое также «дизъюнкцией», либо операцией «ИЛИ», обозначается символом «Ú» или знаком обычного сложения «+».
Используя последнее обозначение, операция ИЛИ символически записывается:
F = х1 +х 2 + … + х n .
Для двух переменных функция принимает вид:
F = х1 + х 2 ,
где х1 и х2 могут принимать значения 0 и 1, как это показано в таблице 2.
Логические элементы, реализующие операцию ИЛИ, называются дизъюнкторами, либо элементами ИЛИ.
Как следует из табл. 2 элемент ИЛИ формирует на выходе единицу тогда и только тогда, когда хотя бы на одном из входов присутствует единица (или на первом, или на втором).
Таблица 2. Таблица истинности двухвходовых элементов ИЛИ, И
| Вход х1 | Вход х2 | Выход ИЛИ | Выход И |
Логическое умножение, называемое также конъюнкцией, либо операцией И, обозначается символом «Ù» либо знаком умножения «·», либо написанием переменных без всякого знака:
F = х1 · х2 · … х n .
Для двух переменных функция принимает вид:
F = х1 · х2.
Логические элементы, реализующие операцию И, называются конъюнкторами, либо элементами И.
Как следует из таблицы 2, элемент И формирует единицу тогда и только тогда, когда на всех его входах присутствует единица (и на первом, и на втором).
Логическое отрицание, называемое также инверсией, либо операцией НЕ, обозначается чертой над переменной F = 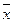 и читается: «F равно не х».
и читается: «F равно не х».
Правило выполнения операции НЕ:
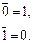
Операция НЕ выполняется логическим элементом, называемым инвертором. Отечественное и зарубежное обозначение рассмотренных логических элементов приведены на рис. 30.

|
| а б в |
| Рис. 30. Обозначения элементов ИЛИ (а), И (б), НЕ (в): отечественные – слева и зарубежные – справа |
Для двух аргументов наряду с дизъюнкцией, конъюнкцией и отрицанием практическое применение находят и другие функции. Все они могут быть выражены через И, ИЛИ, НЕ над двоичными аргументами, однако некоторые из них следует назвать и обозначить особо. Это функции ИЛИ-НЕ, И-НЕ и функции логической неравнозначности. Таблицы истинности этих функций приведены в табл. 3.
Таблица 3.Важнейшие логические функции 2-х переменных
| x1 | x2 | x1↓ x2 | x1│x2 | x1 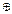 x2 x2
|
Операция ИЛИ-НЕ выполняет сложение с инверсией и обозначается символом «↓». Для двух переменных функция ИЛИ-НЕ примает вид F = x1↓ x2 = 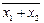 .
.
Из таблицы 3 следует, что функция ИЛИ-НЕ принимает значение единицы тогда и толко тогда, когда все ее аргументы равны нулю.
Опрерация И-НЕ выполняет умножение с инверсией и обозначается символом «│».Для двух переменных функция И-НЕ примает вид F = x1│ x2 = 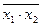 .
.
Как следует из таблицы 3 функция И-НЕ принимает значение единицы тогда и только тогда, когда хотя бы один из ее аргументов равны нулю.
Функция логической неравнозначности (исключающей ИЛИ) принимает значение единицы, если ее аргументы принимают противоположные значения. Для двух переменных функция принимает вид F =x1 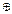 x2 =
x2 = 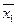 x2 + x1
x2 + x1 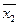 .
.
Отечественные и зарубежные обозначения логических элементов, выполняющие перечисленные операции, приведены на рис.31.

|
| а) б) в) |
| Рис. 31. Обозначения элементов ИЛИ-НЕ (а), исключающее ИЛИ (б), И-НЕ (в): отечественные – слева и зарубежные – справа |
Кроме знаков операции в алгебре Буля применяется знак равенства «=» и скобки. Знак «=» означает не количественное равенство, а то, что разделяемые им выражения равнозначны, поэтому левую часть всегда можно заменить правой и наоборот. Скобки в алгебре Буля, как и в обычной алгебре, указывают на порядок операций. Если скобок нет, то сначала выполняется отрицание над переменными, затем логическое умножение и, наконец, логическое сложение. Когда знак отрицания (черта) ставится над совокупностью символов, операция отрицания выполняется в последнюю очередь.
Логические элементы выпускаются промышленностью в виде интегральных микросхем. В одном корпусе микросхемы могут быть выполнены один, два, три, четыре и шесть логических элементов.
В обозначениях интегральных микросхем логических элементов присутствуют буквы ЛА, ЛИ, ЛЕ, ЛМ и так далее. в зависимости от функции, выполняемой логическим элементом. Например, К1533ЛИ1, 1531ЛА4, КМ555ЛН2.
Основные соотношения, правила и теоремы алгебры Буля
Теоремы для одной переменной. Эти теоремы охватывают все случаи операций над переменной Х и константами 0 и 1 и вытекают из определения операций сложения, умножения, инверсии.
1) х + 0 = х; 5) х · 0 = 0;
2) х + 1 = 1; 6) х · 1 = х;
3) х + х + …+ х = х; 7) х · х · … · х = х;
4) х + 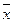 = 1; 8) х ·
= 1; 8) х · 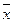 = 0.
= 0.
Теоремы для двух и более переменных. В соответствии с принципом двойственности все теоремы даются в двух вариантах: для логического сложения и для логического умножения. Для краткости изложения все последующие теоремы приведены без доказательств. Применение уже известных теорем алгебры Буля позволит без труда осуществить доказательства любой из теорем.
9) Переместительный закон:
а) х+y = y + х для сложения;
б) х · y = y · х для умножения.
10) Сочетательный закон:
а) х + у + z = х +(у + z) = (х + у) + z;
б) х · у · z = х · (у · z) = (х · у) · z.
11) Распределительный закон:
а) х · (у + z) = х · у + х · z;
б) х + у · z = (х + у) · (х + z).
Теоремы 9, 10, 11 (а) соответствуют законам обычной алгебры. Теорема 11 (б) в обычной алгебре аналога не имеет, но ее, как и теоремы 12–15 нетрудно доказать на основании уже известных теорем алгебры Буля.
12) Без названия:
а) (х + 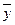 ) · у = ху;
) · у = ху;
б) х · 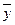 + х = х + y.
+ х = х + y.
Дата добавления: 2015-11-28; просмотров: 2030;
