Применение различных систем счисления в электронных устройствах.

В цифровых системах информация представляется в двоичном (бинарном) коде, состоящем из двух символов: логического «0» и логической «1». Наличие двух символов определяет применение в цифровых устройствах двоичной системы счисления.

Системы счисления, в которых значение каждой цифры определяется не только символом, но и разрядом (позицией в числе N), называют позиционными. Нетрудно заметить, что римская система счисления является непозиционной.

Любое число N в позиционной системе счисления с основанием q можно представить в виде полинома:

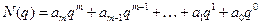
где q - основание системы счисления;

m - номер разряда, отчитываемого от нулевого;

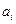- коэффициент i-го разряда (элемента числа N(q)), принимающий значения 0, 1,..., (q-1) - в зависимости от величины N(q).

Например, число 7526(10) в обычной десятичной системе (q=10) может быть представлено в виде:

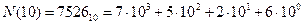
Как видно, коэффициенты нулевого разряда (a₀=6) определяет количество единиц в числе N(10), коэффициент первого разряда (a₁=2) - число десятков и т.д.

Для представления числа в двоичной системе счисления принимаем в основание q=2. Тогда

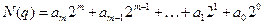
где a_i - коэффициент при разряде, принимающий одно из двух значений (0 или 1) в зависимости от величины N(2).

Например, число 26₁₀ в двоичной системе можно представить в виде:

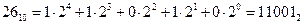
Правило перевода числа из десятичной системы в двоичную заключается в последовательном его делении на 2 (основание двоичной системы) до тех пор, пока частное от деления не станет равным 1. Тогда искомое число в двоичной форме можно сформировать из этого частного и всех остатков, начиная с последнего (справа налево).

В цифровых вычислительных системах используют также комбинированную, десятично-двоичную, систему счисления, облегчающую запись больших чисел с применением двоичного кода. В этом случае каждый разряд десятичного числа записывают двоичным кодом, используя для этого соответствующие тетрады, т.е. четырехразрядные двоичные элементы (числа 8 и 9 иначе представить нельзя). Например, число 197(10) в десятично-двоичной системе имеет вид

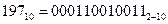
Недостатком рассматриваемой системы является ее избыточность для чисел 7 и менее (недоиспользуются многие двоичные разряды).

Для устранения этого недостатка в ЭВМ используют восьмеричную систему счисления (q=8), которую можно затем записать в двоичном коде (22.5) с использованием для каждой цифры только трех разрядов - триад. Важнейшее свойство восьмеричной системы состоит в следующем: при записи каждого из разрядов восьмеричной системы триадой двоичного кода полученное выражение представляется в двоичной системе счисления.

Восьмеричные системы применяют в ЭВМ для кодирования адресов и команд. Для этого сначала составляют в восьмеричной системе соответствующую программу, а затем переводят ее в двоичную систему, которую и вводят в вычислительную машину.

Еще более удобна шестнадцатеричная (цифро-буквенная) система счисления, которая образуется из десяти цифровых (0,1, ..., 9) и шести буквенных (A, B,..., F) символов. При этом буквы A, B,..., F изображают соответственно числа 10, 11,..., 15. Например, число В7Е₁₆ обозначает:

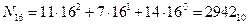
В большинстве ЭВМ число разрядов в группе цифровых символов, несущих некоторую порцию информации (так называемое “машинное слово”), кратно 8. Поэтому информационная емкость машинного слова кратна 8 бит. Единицу количества информации достоинством 8 бит именуют байтом (от английского слова byte - слог), т.е. 1 байт =8 бит. Единицы измерения байт и особенно килобайт (кбайт) находят широкое применение при оценке информационных показателей ЭВМ (объемов памяти и т.п.).

Следует отметить, что под приставкой “кило” в цифровой технике понимают увеличение не в 1000 раз, а в 1024 - число, которое представляет собой десятичную степень числа 2.

Так:

1 Кбайт = 2¹⁰ байт = 1024 байт

1 Мбайт = 2²⁰ байт = 1048576 байт