Операционные элементы
Наряду с рассмотренными ранее комбинационными операционными элементами (сумматор, дешифратор, мультиплексор, преобразователь кода, цифровой компаратор и др.) имеется большая группа последовательностных операционных устройств, таких как регистр, счетчик, арифметико-логические устройства, и др. Наиболее широко распространёнными из них являются регистры.
5.3.1 Регистры
Регистр представляет собой набор триггеров, охваченных общей цепью синхронизации. Триггеры называют разрядами регистра.
По способу ввода / вывода информации регистры делят на:
1) Параллельные (регистры хранения, информация вводится и выводится одновременно по всем разрядам).
2) Последовательные (регистры сдвига, информация бит за битом “проталкивается“ через регистр и выводится также, последовательно бит за битом ).
3) Комбинированные (параллельный ввод, последовательный вывод или наоборот).
По способу представления информации регистры делятся на однофазные и парафазные.
В однофазном регистре информация представляется в прямом или обратном (инверсном) виде, в парафазных - и в том и в другом виде одновременно, то есть в информации всегда имеются нули и единицы.
На рис. 5.2 изображён трёхразрядный регистр хранения на RS-триггерах ( это парафазный регистр, так как есть 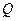 и
и  ):
):
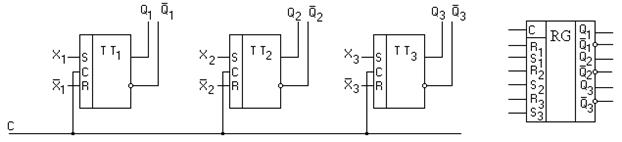
Рисунок 5.2 – Парафазный регистр хранения
Регистр обозначают идентификатором (имя регистра) RG [ 1 – 18 ] , P1[ 1 – 6 ] . Здесь [...] - количество разрядов.
Все входы образуют входную шину, а выходы – выходную шину. Условное обозначение регистра показано на рис. 5.3.
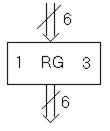
Рисунок 5.3 – Условное обозначение регистра
На операционных схемах регистры и их соединение изображают так, как показано на рис. 5.4.
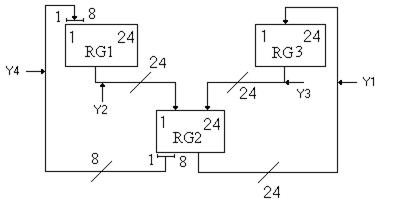
Рисунок 5.4 – Соединение регистров хранения
В этой операционной схеме c тремя 24 – разрядными регистрами выполняются следующие микрооперации передачи:
Y1: RG3: = RG2
Y2: RG2: = RG1
Y3: RG2: = RG3
Y4: RG1[1-8] : = RG2 [1-8]
Часть разрядов в регистре, которые носят самостоятельное значение называются субрегистром или подрегистром ( RG2[ 1-8] – подрегистр регистра RG2[1-24] ). Регистры хранения могут выполнятся на триггерах любых типов.
Синтез регистров хранения.
Возьмем два четырёхразрядных регистра хранения на JK-триггерах и соединим их между собой с помощью конъюнкторов (рис. 5.5).
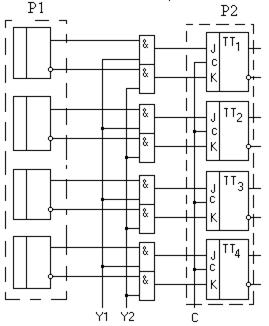
Рисунок 5.5 – Соединение регистров с помощью конъюнкторов
Входы Y1 и Y2 являются дополнительными управляющими входами. На операционных схемах такое соединение регистров условно обозначают следующим образом (рис. 5.6)
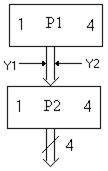
Рисунок 5.6 – Соединение регистров на операционных схемах
Рассмотрим, как будут влиять сигналы Y1 и Y2 на передачу информации с регистра P1 на регистр Р2.
Пусть, например, Y1=Y2=0. Тогда P2 находится в режиме хранения своей информации, так как на выходах всех конъюнкторов имеются нули (на входах J = K = 0 ). Если Y1=1, Y2=0, то на входах К =0 (нижние конънкторы), а состояние входов J рассмотрим по таблице (рис. 5.7), в которой состояние регистра определяется прямыми выходами триггеров:
| Такт t | Такт t+1 | ||
| P1 | P2 | Входы P2 | Регистр Р2 |
Рисунок 5.7 – Состояния входов и выходов регистра Р2
Если на входе J = 1, то на выходе Р2 тоже будет единица. Таким образом , выполняется микрооперация дизъюнкции над содержимым регистров
Y1: Р2 : = Р1 V Р2.
Возьмём другой случай Y1= 0, Y2 = 1 (рис. 5.8).
| Такт t | Такт t+1 | ||
| P1 | P2 | Входы P2 | Регистр Р2 |
Рисунок 5.8 – Состояния входов и выходов регистра Р2
Видно, что выполняется другая микрооперация, а именно – конъюнкция
Y2: P2 : = P1 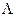 P2
P2
Нетрудно видеть, что если Y1=Y2=1, то Р1: = Р2, то есть выполняется микрооперация передачи.
Мы выполнили анализ регистра, то есть, соединили регистры и ответили на вопрос что будет при таком соединении.
На практике обычно ставится задача не анализа, а синтеза, то есть, как соединить регистры между собой, чтобы выполнялась требуемая микрооперация.
Синтез регистра сводится к синтезу одного разряда, так как все остальные разряды идентичны. Пусть, например, требуется синтезировать регистр на Т-триггерах для выполнения следующих микроопераций между входной информацией и содержимым регистра:
1) Передача 2) Дизьюнкция ( V ) 3) Конънкция ( 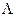 )
)
Составим схему (рис. 5.9):
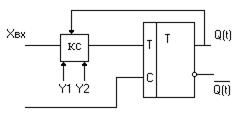
Рисунок 5.9 – Схема для синтеза одного разряда регистра
Здесь КС – комбинационная схема.
Составим таблицу истинности работы нашего устройства, но сначала необходимо произвольно закодировать управляющие сигналы (рис. 5.10):
| Y1 | Y2 | Микрооперация |
| Передача | ||
| V | ||
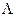
|
Рисунок 5.10 – Кодировка микроопераций
Составляем таблицу истинности для дальнейшего синтеза (рис. 5.11)
| Xвх | Y1 | Y2 | Q(t) | Q(t+1) | 
|
| * | - | ||||
| * | - | ||||
| * | - | ||||
| * | - | ||||
Рисунок 5.11 – Таблица истинности для синтеза регистра
На основании словаря переходов Т-триггера (рис. 5.12) заполняем колонку с сигналом T* - выходным сигналом комбинационной схемы
| Q(t) | T | Q(t+1) |
Рисунок 5.12 – Словарь переходов Т - триггера
Составим карту Карно (рис. 5.13) и минимизируем функцию для Т*
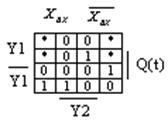
Рисунок 5.13 – Карта Карно для регистра
Получаем минимальную форму
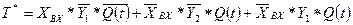 ,
,
по которой составляем комбинационную схему одного разряда регистра (рис. 5.14)
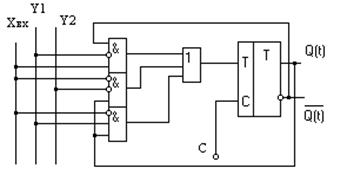
Рисунок 5.14 – Схема одного разряда регистра
По такому алгоритму регистры хранения можно создавать для выполнения различных микроопераций на триггерах любого типа.
Регистры сдвига.
Служат для сдвига кода слова, занесённого в регистр. В зависимости от направления сдвига регистры делят на:
1) регистры со сдвигом вправо.
2) регистры со сдвигом влево.
3) реверсивные регистры.
Причём, различают ещё и сдвиги - арифметические, логические и циклические.
При арифметическом сдвиге смещаются все разряды кода, кроме знакового (крайнего левого бита). При логическом сдвиге смещаются все разряды кода, включая знаковый бит. При циклическом сдвиге крайние разряды соединены между собой, поэтому выдвигающийся бит помещается на освободившееся место.
При арифметическом и логическом сдвигах выдвигающиеся биты теряются, а освободившиеся места заполняются нулями.
Микрооперация сдвига записывается следующим образом:
Y1: P2:= сдв ЛП (2) P2 - сдвиг логический вправо на два бита содержимого регистра Р2
Y2: P1:= сдв АЛ (1) P1 - сдвиг арифметический влево на один бит содержимого регистра Р1
Y3: RG : = сдв ЦП (1) RG – сдвиг циклический вправо на один бит содержимого регистра RG.
Регистр сдвига наиболее просто выполнить на D – триггерах (рис. 5.15).
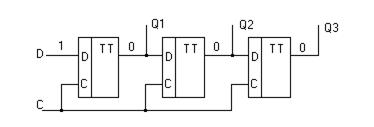
Рисунок 5.15 – Регистр сдвига
С приходом синхроимпульса код смещается вправо на один разряд. Регистр сдвига можно выполнить на JK-триггерах. Для чего организуют D- вход (рис. 5.16)

Рисунок 5.16 – Регистр сдвига на JK - триггерах
Так как цепь синхронизации является общей для всего блока (или узла), а микрооперацию сдвига требуется выполнить не всегда, то делают дополнительный вход через конъюнктор (рис. 5.17). При V=1 сдвиг будет выполнен по синхросигналу. При V=0 сдвига не будет.
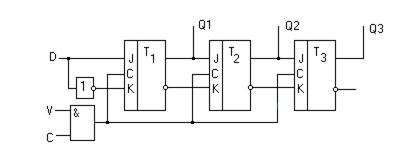
Рисунок 5.17 – Регистр сдвига на JK – триггерах c конъюнктором
Поэтому, регистры сдвига удобно выполнять на DV-триггерах (рис. 5.18). На вход V подают сигнал микрооперации сдвига.

Рисунок 5.18 – Регистр сдвига на DV – триггерах
Регистр сдвига на операционной схеме обозначают так (рис. 5.19)
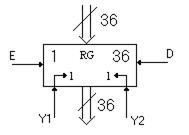
Рисунок 5.19 – Регистр сдвига на операционной схеме
На этом рисунке обозначено: Y1 - микрооперация сдвига вправо на 1 бит; Y2 - микрооперация сдвига влево на 1 бит; Д, Е - дополнительная информация, которая помещается в освобождающиеся разряды. Тогда происходит составление нового слова на регистре
Y1: P1: = сдв ЛП (1) P2 I E 
Y2: P2: = сдв ЛЛ (1) P2 I D
Микрооперация составления нового слова называется конкатенаций.
Регистры сдвига широко используются для организации последовательных АЛУ, преобразований кодов и выпускаются в виде отдельных микросхем
( К155ИР1, К155ИР11 и др.).
Если вход и выход регистра сдвига соединить между собой, то код будет непрерывно циркулировать по замкнутому контуру, получается так называемый динамический регистр. Возьмём трёхразрядный регистр сдвига (рис. 5.20).
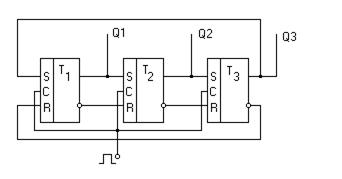
Рисунок 5.20 – Динамический регистр
Пусть в исходном состоянии на регистре записан код 1 0 0 (такт № 0). В каждом последующем такте эта единица будет перемещаться (рис.5.21)
| Такт | Q1 | Q2 | Q3 | tцсх<tцц | tцсх>tцц | ||||
Рисунок 5.21 – Движение кода в динамическом регистре
Видно, что код на регистре повторяется через n-тактов, где n = 3 - число разрядов регистра.
Существуют два понятия:
1) Период циркуляции кода на регистре. Он равен числу разрядов (tцц = n ).
2) Период цикла схемы - это время, через которое код считывается из регистра (t цсх).
В зависимости от соотношения tцц и tцсх возможны три режима работы:
1) tцц = tцсх - это режим хранения информации.
2) tцсх < tцц - режим сдвига влево (регистр со сдвигом влево ).
3) tцсх > tцц - регистр со сдвигом вправо.
Получился универсальный регистр, но быстродействие его невысокое.
Динамические n – разрядные регистры соединяются в блоки по m штук (как показано на рис. 5.22) и записывают в них слова “поперёк”. Всего можно записать n штук m – разрядных слов. Эти слова появляются в некотором сечении регистров через время равное n тактов. Получили, так называемую, регистровую память или цифровую линию задержки (ЦЛЗ).
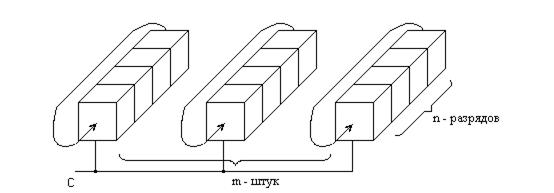
Рисунок 5.22 – Цифровая линия задержки
Для этих целей специально выпускаются регистры. Например, микросхема К144ИР3 – регистр на 64 бит (задержка на 64 такта).
5.3.2 Счетчики
Счетчик – это узел ЭВМ, предназначенный для подсчета числа входных сигналов. Счетчик выполняет микрооперацию счет Сч =Сч 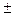 1.
1.
Счетчики характеризуются рядом параметров:
1) Модуль счета - М. Это число устойчивых состояний счетчика. Если М кратно 2 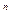 , где n-число разрядов (триггеров), то счётчик называется двоичный. Иначе - счётчик с произвольным модулем (основанием) счёта.
, где n-число разрядов (триггеров), то счётчик называется двоичный. Иначе - счётчик с произвольным модулем (основанием) счёта.
2) Емкость - Е. Это максимальное число, которое может быть записано в счетчик E = M – 1.
3) Быстродействие или скорость перехода из состояния 11...111 в состояние 00...000 или наоборот.
Счетчики классифицируют по таким признакам:
1) По направлению счета (суммирующие, вычитающие и реверсивные).
2) По способу построения цепи переноса (c последовательным переносом, с параллельным переносом и комбинированные).
3) По способу опрокидывания триггеров (асинхронные и синхронные).
Простейший суммирующий асинхронный двоичный счетчик строится на
Т-триггерах. Например, трёхразрядный счетчик (рис.5.23).
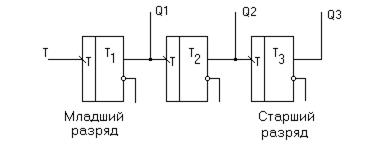
Рисунок 5.23 – Простейший суммирующий счётчик
Диаграмма его работы приведена на рис. 5.24. Из неё видно, что если двоичное число читать снизу вверх, то это число увеличивается на единицу с приходом очередного сигнала на вход Т. Модуль счёта М = 8, а емкость Е = 7. Если информацию снимать с инверсных выходов триггеров, то мы получаем вычитающий счетчик.
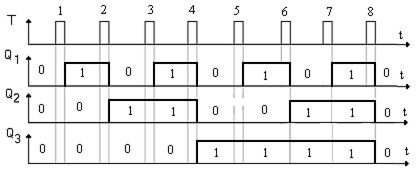
Рисунок 5.24 – Диаграмма работы счётчика
Составим схему такого же счетчика, но на триггерах с прямым типом управления (рис. 5.25):
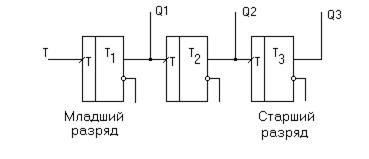
Рисунок 5.25 – Простейший вычитающий счётчик
Здесь триггеры опрокидываются по переднему фронту входного сигнала, поэтому диаграмма работы будет следующая (рис. 5.26).
Получили вычитающий счетчик. Если выходные сигналы снимать с инверсных выходов триггеров, то будет суммирующий счетчик.
Это счетчик с так называемым последовательным переносом, так как перенос распространяется последовательно от разряда к разряду.
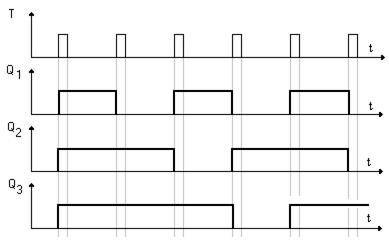
Рисунок 5.26 – Диаграмма работы
Быстродействие такого счётчика определяется временем опрокидывания всех разрядов (рис. 5.27) и примерно равно произведению времени срабатывания одного триггера (tср) и числа разрядов (n).
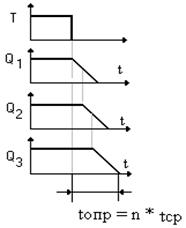
Рисунок 5.27 – Опрокидывание всех разрядов счётчика
Асинхронные счетчики с последовательным переносом имеют низкое быстродействие, поэтому чаще используют синхронные счетчики.
Трёхразрядный синхронный суммирующий счетчик(рис. 5. 28).
Счётчик строится на синхронных Т - триггерах. Счётные импульсы поступают  на вход С. Все триггеры опрокидываются одновременно, по сигналу С.
на вход С. Все триггеры опрокидываются одновременно, по сигналу С.

Рисунок 5.28 – Синхронный счётчик
Здесь t опр 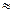 t ср – время опрокидывания счётчика не зависит от количества разрядов, но по сути этот счетчик остается счетчиком с последовательным переносом.
t ср – время опрокидывания счётчика не зависит от количества разрядов, но по сути этот счетчик остается счетчиком с последовательным переносом.
Несколько большими возможностями обладают счетчики с параллельным переносом. Трёхразрядный счетчик с параллельным переносом (рис. 5.29).
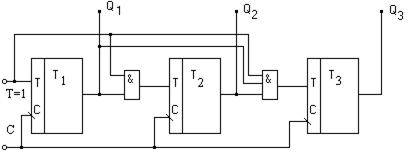
Рисунок 5.29 – Синхронный счётчик с параллельным переносом
Здесь, когда сигнал Т = 1, то выполняется счет, когда Т=0, на выходах всех конъюнкторов будут нули и все триггеры счетчика будут находится в режиме хранения информации, то есть сигнал Т - это сигнал микрооперации счета:
Т: Сч: = Сч + 1
Быстродействие t опр = t ср.
Счетчик хороший, но с увеличением числа разрядов, возрастает сложность конъюнкторов, поэтому многоразрядный счетчик разбивают на группы по 4 или 8 разрядов. Внутри группы делают параллельный или последовательный перенос, а между группами параллельный. Такой счетчик называется счетчиком с групповым переносом. На операционных схемах счетчик обозначают следующим образом (рис.5.30):
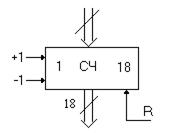
Рисунок 5.30 – Обозначение счётчика на операционных схемах
Здесь + 1 - вход для работы на сложение.
- 1 - вход для работы на вычитание.
R – вход установки всех разрядов счетчика в нуль.
Счетчики выполняются в виде отдельных микросхем. Например, четырёхразрядный двоичный реверсивный счетчик К155ИЕ7 (рис. 5.31)
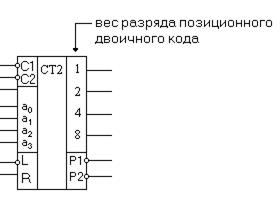
Рисунок 5.31 – Пример микросхемы счётчика
На этой схеме: C1,C2 – синхровходы (C1-для работы на сложение, C2-для работы на вычитание), A1,A2,A3,A4 - входы для начальной записи информации в счетчик, R-сброс всех разрядов счетчика в ноль, L-управление режимом. При L=0 запись информации по входам А. При L=1 выполняется счет. Р1-выход переноса при работе на сложение, Р2-выход единицы заёма при работе на вычитание.
Счётчик выполнен на RST-триггерах. Выходы Р1 и Р2 служат для наращивания разрядности счётчика.
Различные области использования счетчиков требуют различных модулей счета не кратных  , то есть это счетчики с произвольным модулем счета К.
, то есть это счетчики с произвольным модулем счета К.
Построить такие счётчики можно тремя способами.
1) Использование стандартного двоичного счетчика с модулем М =  большим, чем требуемый модуль К.
большим, чем требуемый модуль К.
Допустим, нам нужен счетчик с модулем 17. Тогда требуется пятиразрядный двоичный счетчик (n =5 ).
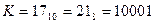 . На выход подключаем конъюнктор (рис. 5.32).
. На выход подключаем конъюнктор (рис. 5.32).
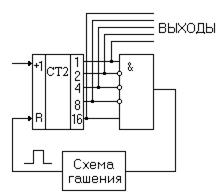
Рисунок 5.32 – Счётчик с произвольным модулем счёта
Когда код на счётчике будет равен К = 10001, то на выходе конъюнктора появляется единица, которая запускает схему гашения. Длительность импульса схемы гашения должна быть достаточной для надёжного сброса всех триггеров счётчика, иначе код на счётчике будет неправильным. Для другого модуля К, конъюнктор будет другим (рис. 5.33)
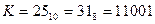
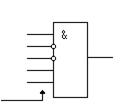
Рисунок 5.33 – Конъюнктор для счётчика
Схема гашения выполняется на RS – триггере, как это показано на рис. 5.34
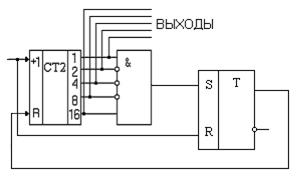
Рисунок 5.34 – Схема гашения на RS - триггере
Сигнал на входе R счётчика будет действовать в течение одного периода счётных импульсов.
Достоинства: используется стандартный счётчик; естественный ход нарастания кода на счетчике.
Недостаток: требуется схема гашения. Невозможность изменения модуля счета без переделки схемы.
2) Использование стандартного счетчика с 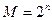 > К, в который загружают начальное число ( исходный код ) и работают либо на сложение до естественного переполнения счётчика, либо на вычитание до обнуления счётчика (рис. 5.35), после этого в счетчик снова загружается исходный код.
> К, в который загружают начальное число ( исходный код ) и работают либо на сложение до естественного переполнения счётчика, либо на вычитание до обнуления счётчика (рис. 5.35), после этого в счетчик снова загружается исходный код.
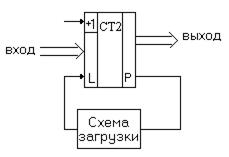
Рисунок 5.35 – Второй способ построения счётчика
Достоинства этого способа: использование штатной цепи переноса; легко программировать модуль и изменять его в процессе работы.
Недостатки: начало счета соответствует некоторому числу, поэтому нет естественного изменения кода; необходима схема загрузки.
3) Прямой синтез счетчика на триггерах заданных типов.
Этот способ используется в специальной аппаратуре, а также для построения устройств управления операционными элементами, где счётчики вырабатывают сигналы микроопераций.
Пусть, например, требуется синтезировать счетчик по произвольному основанию (с модулем М=6).
Порядок смены состояний такой: 001, 010, 011, 100, 110 , 111.
Младший разряд выполнить на RS-триггере, а два других на D и T - триггерах.
Составим таблицу истинности работы счетчика (рис. 5.36).
| № | Такт t | Такт t+1 | Функции возбуждения | ||||||
| Q1 | Q2 | Q3 | Q1 | Q2 | Q3 | T | D | R S | |
| 1 0 | |||||||||
| 0 1 | |||||||||
| 1 0 | |||||||||
| - 0 | |||||||||
| 0 1 | |||||||||
| 0 - |
Рисунок 5.36 – Таблица истинности счётчика и функции возбуждения
Функции возбуждения триггеров заполним на основании словарей переходов наших триггеров (рис.5.37).
| Q(t) | D | T | RS | Q(t+1) |
| - 0 | ||||
| 0 1 | ||||
| 1 0 | ||||
| 0 - |
Рисунок 5.37 – Словари переходов триггеров
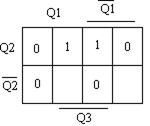
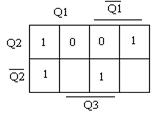
Составим карты Карно для каждого сигнала возбуждения (рис. 5.38).
Т–триггер: D–триггер:
RS – триггер:
Вход R Вход S
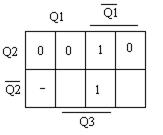
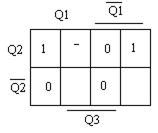
Рисунок 5.38 – Карты Карно для управляющих входов триггеров
На основании этих карт записываем минимальные формы 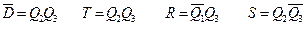 , по которым составляем схему счетчика.
, по которым составляем схему счетчика.
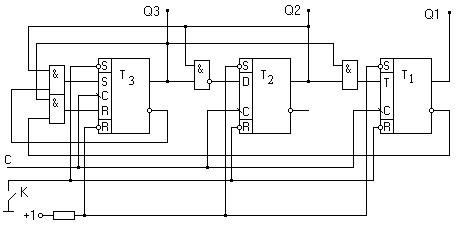
Рисунок 5.39 – Принципиальная схема счётчика на триггерах
Ключ К служит для установки счётчика в начальное состоянии Q1Q2Q3 = 0 0 1 путём его кратковременного замыкания.
5.3.3 Арифметико – логические устройства
Арифметико-логические устройства (АЛУ) служат для выполнения арифметических и логических операций над словами, называемых операндами.
АЛУ современных вычислительных машин выполняют такие группы операций:
- двоичная арифметика с фиксированной запятой;
- двоичная арифметика с плавающей запятой;
- десятичная арифметика;
- логические операции;
- специальная арифметика (нормализация чисел, сдвиги и др.);
- операции над алфавитно – цифровыми полями.
Мини, микро ЭВМ и микропроцессоры все операции выполняют в двоичной системе счисления над числами с фиксированной запятой. Другие группы операций выполняются, как правило, программным способом, то есть с использованием специальных подпрограмм.
По характеру использования элементов АЛУ делят на блочные и многофункциональные. В блочныхАЛУ, каждая группа операций выполняется отдельным блоком, которые могут работать одновременно. Повышается быстродействие, но возрастают и затраты оборудования.
В многофункциональныхАЛУ все операции выполняются одними и теми схемами, которые коммутируются в зависимости от требуемой операции. Поэтому, возрастает степень использования оборудования, но быстродействие ниже, чем в блочных АЛУ.
По своим функциям АЛУ является операционным блоком и широко используется для построения арифметических узлов, в частности, АЛУ входит в состав любого микропроцессора.
Рассмотрим схему АЛУ для сложения чисел с фиксированной запятой, передаваемых по общей шине. Она приведена на рис. 5.40.
Основой АЛУ является n – разрядный комбинационный сумматор. Операнды поступают по общей входной шине в регистры РА и РВ, которые поочерёдно подключают к шине с помощью тристабильных элементов. Первое слагаемое (уменьшаемое) помещается в регистре РВ. Второе слагаемое (вычитаемое) помещается в регистре Р1, который связан с регистром РА цепями прямой и инверсной передачи кода. Прямая передача используется при сложении, а инверсная при вычитании (выполняется сложение в дополнительном коде). Операция вычитания заменяется сложением: Z = X - Y = X + (-Y), а в младший разряд результата добавляется единица. Результат выдаётся в регистр Р2.
Комбинационная схема (КС) следит за переносами в знаковый разряд и из него и вырабатывает признак результата - ПР (флаг): больше нуля (ПР =01), меньше нуля(ПР =10), равно нулю (ПР = 00), переполнение разрядной сетки (ПР =11).
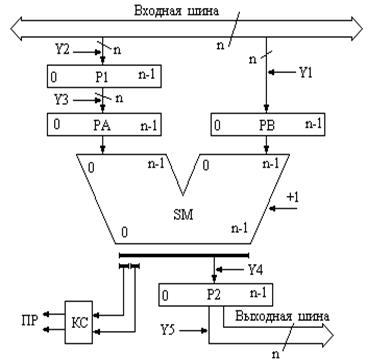
Рисунок 5.40 – Схема АЛУ для сложения чисел
Составим микропрограмму сложения двух чисел.
Y1: РВ = 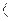 слово1
слово1 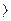


Y2: Р1 = 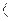 слово2
слово2 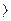


Y3: РА = Если сложение то Р1 иначе 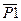
Y4: Р2 = Если сложение то РА + РВ иначе РА+ РВ + 1
Y5: Если ПР = 11 то переполнение иначе 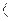 вых. шина
вых. шина 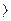 = Р2
= Р2
Конец
Для выполнения операций умножения, деления, логических операций схема АЛУ дополняется другими элементами.
Дата добавления: 2016-01-18; просмотров: 2308;
