Мультиплексор и демультиплексор

Мультиплексор (коммутатор) это многовходовая комбинационная схема служит для коммутации одного из 2ⁿ информационных входов на выход под действием n управляющих (адресных) сигналов.

Составим схему мультиплексора при n = 2 (рис. 3.10).

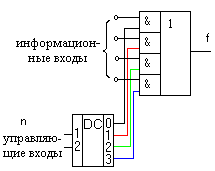
Рисунок 3.10 – Схема мультиплексора

Мультиплексор реализует дизъюнкцию элементарных конъюнкций и является универсальным устройством.

,

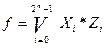где Z_i – информационный сигнал, X_i – сигналы с выхода декодера. Условное обозначение мультиплексора (рис. 3.11 а ):

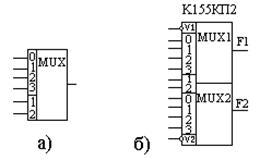
Рисунок 3.11 – Условное обозначение и пример микросхемы

Мультиплексоры выпускаются как отдельные микросхемы. Например, сдвоенный четырёхканальный мультиплексор К155КП2 (рис.3.11 б), который имеет общий декодер на оба канала.

Промышленностью выпускаются мультиплексоры с числом адресных входов 2, 3, 4. Если этого недостаточно, то используют их каскадное включение.

Пусть требуется создать 16и – канальный мультиплексор из 4х – канальных. Значит адрес должен быть четырёхразрядным Х Х Х Х ( 2 = 16 ). Этот адрес подаётся на входы декодеров определённым образом (рис. 3.12)

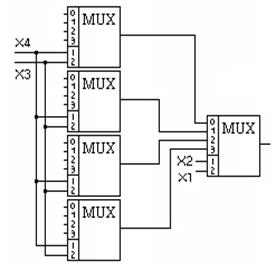
Рисунок 3.12 – Мультиплексор на 16 каналов (16 в 1)

Так как мультиплексор выполняет дизъюнкцию элементарных конъюнкций, то с его помощью можно реализовать любые функции алгебры логики. Пусть, например, задана функция алгебры логики F такой таблицей истинности (рис. 3.13):

№	а	b	c	F	D
					C

Рисунок 3.13 – Таблица истинности и входные сигналы D

Возьмем 4-х канальный мультиплексор. Старшую переменную подаем на старший вход декодера, на младший вход декодера поступает следующая переменная. Младшая переменная (С) подаётся на информационные входы, но в зависимости от значения самой ФАЛ. Так, на вход № 0 , определяемый переменными a,b (00), подадим сигнал С, поскольку значения F и C совпадают. На вход № 1 ( 01 ) – сигнал “не С”, поскольку значения F и C противоположны. На вход № 2 ( 10) – сигнал “0”, поскольку значения F не зависят от С и равны нулю. На вход №3 (11) – 1. Тогда реализация исходной ФАЛ будет такой (рис. 3.14)

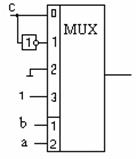
Рисунок 3.14 – Реализация ФАЛ на мультиплексоре

С точки зрения математики безразлично, какие переменные подавать на адресные входы, а какую переменную на информационные, но с точки зрения практики нет. На информационные входы следует подавать ту переменную, от которой в наименьшей степени зависит МДНФ функции. Это делается для того, чтобы не перегружать выходы источника сигнала. Проверим правильно ли мы поступили ?

Найдем МДНФ нашей функции по карте Карно (рис. 3.15).

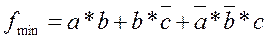
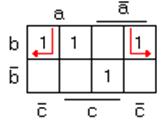
Рисунок 3.15 – Карта Карно исходной ФАЛ

В минимальной форме переменная “а” встречается 2 раза, переменная “b” – 3 раза, переменная ”c” – 2 раза. Значит, на информационные входы можно подавать “a” или “c”. Мы поступили верно. Теперь реализуем схему по переменной “а”.

Здесь номер информационного входа задают переменные “bc”, а значение ФАЛ надо сравнивать с переменной “a”. Тогда получим другую реализацию (рис. 3.16).

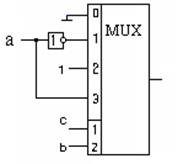
Рисунок 3.16 – Второй вариант реализации ФАЛ

Демультиплексор.

Выполняет функцию обратную мультиплексору, то есть коммутирует один информационный вход на один из 2ⁿ выходов под действием n управляющих (адресных ) сигналов. Составим схему демультиплексора при n = 2 (рис. 3.17).

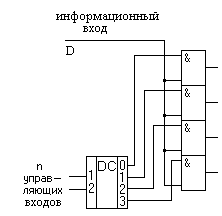
Рисунок 3.17 – Демультиплексор на 4 канала

Очевидно, что если на информационный вход (D) подать 1, то это будет дешифратор в чистом виде. Вход D можно использовать как клапан (V) (рис.3.18)

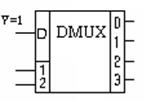
Рисунок 3.18 – Обозначение демультиплексора

Микросхемы так и называются дешифратор – демультиплексор. Например, ИМС КР531ИД14.

Сумматоры

Сумматор – это узел ЭВМ, предназначенный для сложения кодов двоичных чисел. Сумматоры делятся на последовательные (накапливающие) и параллельные (комбинационные). Накапливающие сумматоры имеют низкое быстродействие, поэтому они рассматриваться не будут. В комбинационных сумматорах слагаемые поступают на входы одновременно, а на выходе получается код суммы. После снятия слагаемых результат пропадает. Эти устройства не обладают памятью и строятся на логических элементах.

Составим таблицу истинности устройства для сложения двух одноразрядных чисел a и b (рис. 3.19)

Рисунок 3.19 – Таблица истинности для сложения двух цифр

Здесь р – перенос в старший разряд, s – значение суммы. Устройство, реализующее эту таблицу истинности, называют двоичным полусумматором. Его можно синтезировать по ФАЛ для каждого из выходов

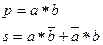
Составим схему на произвольных элементах (рис. 3.20)

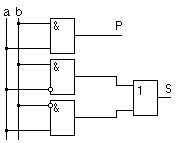
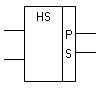
Рисунок 3.20 – Схемная реализация и условное обозначение

полусумматора

При сложении многоразрядных чисел необходимо складывать три двоичных цифры в каждом разряде – два слагаемых и единицу переноса из предыдущего разряда Pi-1. Наличие этой единицы переноса несколько меняет таблицу сложения двоичных чисел (рис. 3.21):

Рисунок 3.21 – Таблица истинности для сложения трёх цифр

Система собственных функций:

для суммы: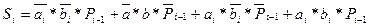

для переноса (рис. 3.22):

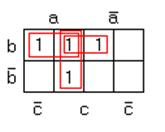
Рисунок 3.22 – Карта Карно для цепи переноса

Минимальная форма по этой карте .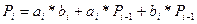

Уравнение для S_i не минимизируется. Устройство, реализующее эти ФАЛ называется сумматор (полный сумматор ). Он имеет три входа и два выхода. Цена сумматора по уравнениям составляет Ц = 25. Путем совместной минимизации уравнений S_i и P_{i ,} удается снизить цену до 20 и, в таком виде, выпускаются микросхемы сумматоров. Например, К155ИМ1 – полный одноразрядный сумматор (рис. 3.23).

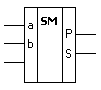
Рисунок 3.23 – Полный сумматор

Для сложения многоразрядных чисел сумматор составляют из одноразрядных. Пусть требуется сложить два четырёхразрядных двоичных числа: А и В

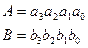
Составим схему сумматора (рис. 3.24)

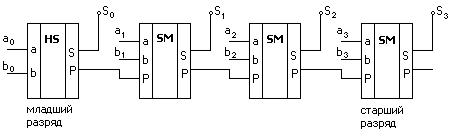
Рисунок 3.24 – Многоразрядный сумматор

Получился многоразрядный сумматор с последовательным переносом.Такие сумматоры выпускают в виде отдельных микросхем. Например, ИМС К155 ИМ3 - четырёхразрядный сумматор с последовательным переносом. Время сложения чисел определяется временем распространения переноса и равно 55 нсек (для четырёх разрядов).С ростом числа разрядов быстродействие сумматора

уменьшается, так как цепь переноса последовательная.

Вспомним формулу переноса

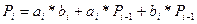
Найдём эти переносы

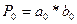
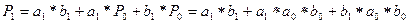
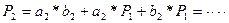
Видно, что имея только слагаемые можно формировать перенос в любом разряде не дожидаясь его появления в предыдущем разряде, причём с помощью только двухуровневой схемы (один слой конъюнкторов и один дизъюнктор ). Такая схема называется схема ускоренного переноса(параллельного переноса). Она может быть встроена в сумматор (сумматор с параллельным переносом) или выпускаться отдельно. Например, ИМС К155 ИМ6 – четырёхразрядный сумматор с параллельным переносом. Время сложения чисел равно 27 нсек.

При большом числе разрядов сложность схемы ускоренного переноса сильно возрастает. Поэтому сумматор разбивают на группы по 4 или 8 разрядов. Внутри группы выполняют параллельный перенос, а между группами - параллельный или последовательный. Такие сумматоры называют сумматоры с групповым переносом.

Многоразрядный сумматор условно обозначают так (рис. 3.25)

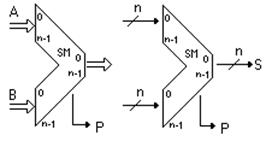
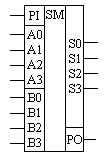
Рисунок 3.25 – Условное обозначение многоразрядного сумматора

С помощью сумматоров можно не только складывать, но и вычитать двоичные числа. При использовании дополнительных кодов операцию вычитания двух положительных чисел заменяют операцией суммирования положительного и отрицательного чисел, при этом получение дополнительного кода числа является элементарной операцией. Для этого необходимо проинвертировать число и прибавить к нему в младший разряд 1.

Схема вычитателя числа A из числа B приведена на рисунке 3.26, а схема вычитателя числа B из числа A приведена на рисунке 3.27.

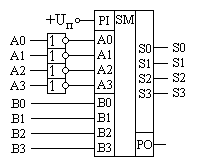
Рисунок 3.26. Схема вычитателя числа A из числа B

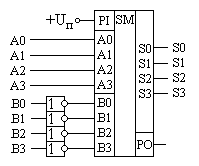
Рисунок 3.27. Схема вычитателя числа B из числа A.

Схема инкремент/декремент.

Возьмём три полусумматора и соединим их следующим образом (рис.3.28)

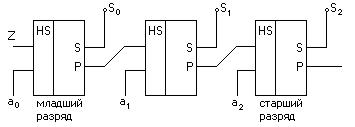
Рисунок 3.28 – Схема инкремент / декремент

Подавая на управляющий вход Z ноль или единицу, проанализируем состояние выхода при различных входных сигналах (рис. 3.29)

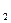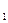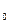
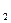Z	Входной код а а а	Выходной код S 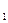S S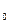

Рисунок 3.29 – Соответствие сигналов схемы инкремент / декремент

Если на вход Z поступает 0, то число на выходе будет без изменений. Если на вход Z подать 1, то эта единица добавляется к младшему разряду числа (инкремент +1).

Если числа на входе и выходе проинвертировать, то мы получаем схему декремент (декремент -1).

A₂ A₁ A₀ S₂ S₁ S₀

Число на входе 1 1 0 1 0 1 получился ответ

Выполняем инверсию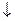

0 0 1 инкремент 0 1 0

Эта схема самостоятельного значения не имеет, но широко используется как составная часть арифметико – логических устройств.