ИНЕРЦИОННОЕ ОСАЖДЕНИЕ ЧАСТИЦ
При обтекании твердого тела (или капли) запыленным потоком частицы вследствие большей инерции продолжают двигаться поперек изогнутых линий тока газов (рис. 2.5) и осаждаются на поверхности тела. Такое осаждение называется инерционным. Коэффициент эффективности инерционного осаждения ηStk определяется долей частиц, извлеченных из потока, при обтекании им тела. Иногда его называют «эффективностью мишени».
Траектория движения частицы в газовом потоке может быть описана уравнением
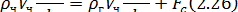
где  - объем частицы, м3; τ- время движения, с;
- объем частицы, м3; τ- время движения, с; 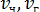 - вектор скорости соответственно частицы и газов в месте нахождения частицы, м/с.
- вектор скорости соответственно частицы и газов в месте нахождения частицы, м/с.
Если газовый поток движется стационарно, а частица настолько мала, что для 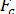 применим закон Стокса (включая поправку Кенингема - Милликена), уравнение (2.26) можно записать в следующем виде:
применим закон Стокса (включая поправку Кенингема - Милликена), уравнение (2.26) можно записать в следующем виде:

где 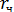 - радиус-вектор частицы, м.
- радиус-вектор частицы, м.
Уравнение (2.27) удобно привести к безразмерному виду, введя следующие обозначения:
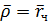 /
/ 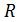 - безразмерная координата частицы, где
- безразмерная координата частицы, где 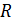 - характерный размер обтекаемого тела (например, радиус шара или цилиндра в м);
- характерный размер обтекаемого тела (например, радиус шара или цилиндра в м); 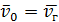 /
/  -безразмерная скорость газов, где
-безразмерная скорость газов, где  - скорость газов вдали от обтекаемого тела в м/с;
- скорость газов вдали от обтекаемого тела в м/с;  (
(  /
/ 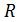 )
)  - безразмерное время.
- безразмерное время.
Тогда после соответствующих подстановок и упрощений получим

где 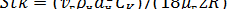 - критерий Стокса, или «инерционный параметр», характеризующий отношение инерционной силы, действующей на частицу к силе гидравлического сопротивления среды. Критерий численно равен отношению расстояния, проходимого частицей с начальной скоростью υгпри отсутствии внешних сил до остановки
- критерий Стокса, или «инерционный параметр», характеризующий отношение инерционной силы, действующей на частицу к силе гидравлического сопротивления среды. Критерий численно равен отношению расстояния, проходимого частицей с начальной скоростью υгпри отсутствии внешних сил до остановки 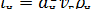 /
/  к характерному размеру обтекаемого тела (например диаметру шара или цилиндра).
к характерному размеру обтекаемого тела (например диаметру шара или цилиндра).
Если движение частицы осуществляется в области, где закон Стокса неприменим, необходимо ввести поправку, учитывающую отношение истинной силы сопротивления к стоксовскому сопротивлению, равную 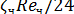

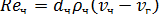 /
/ 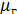 - критерий Рейнольдса для частицы.
- критерий Рейнольдса для частицы.
Критерий 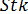 является единственным критерием подобия инерционного осаждения. Это означает, что уравнение (2.28) применимо к геометрически подобным системам с одинаковым значением Re; в этом случае подобие конфигураций линий тока будет соблюдено вне зависимости от различий между скоростями движения.
является единственным критерием подобия инерционного осаждения. Это означает, что уравнение (2.28) применимо к геометрически подобным системам с одинаковым значением Re; в этом случае подобие конфигураций линий тока будет соблюдено вне зависимости от различий между скоростями движения.
Из уравнения (2.28) следует, что при 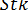 = 0 (у частиц с бесконечно малой массой)
= 0 (у частиц с бесконечно малой массой)  /
/ 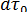 т. е. частица точно следует по линии тока, не соприкасаясь с поверхностью обтекаемого тела. Очевидно, такое же явление будет наблюдаться и при достаточно малых значениях критерия Стокса. Существует определенное минимальное, так называемое критическоезначение числа Стокса
т. е. частица точно следует по линии тока, не соприкасаясь с поверхностью обтекаемого тела. Очевидно, такое же явление будет наблюдаться и при достаточно малых значениях критерия Стокса. Существует определенное минимальное, так называемое критическоезначение числа Стокса 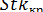 , при котором инерция частицы оказывается достаточной, чтобы преодолеть увлечение ее газовым потоком, и она достигает поверхности тела. Таким образом, захват частицы телом возможен при условии:
, при котором инерция частицы оказывается достаточной, чтобы преодолеть увлечение ее газовым потоком, и она достигает поверхности тела. Таким образом, захват частицы телом возможен при условии: 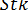 >
> 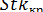 .
.
Следует отметить, что теория инерционного осаждения рассматривает осаждение частиц на фронтальной (передней) части обтекаемого тела и не учитывает их осаждение на задней поверхности тела, которое может происходить за счет турбулентных пульсаций газового потока. Это явление становится существенным при малых значениях критерия 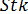 , т. е. при улавливании субмикронных частиц пыли. Поэтому даже при
, т. е. при улавливании субмикронных частиц пыли. Поэтому даже при 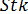 <
< 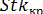 эффективность осаждения не равна нулю.
эффективность осаждения не равна нулю.
Траектория движения частицы, включая крайние траектории, может быть определена с помощью уравнения (2.28). Однако проинтегрировать это уравнение в общем виде пока не удалось.
По рис. 2.5 легко проследить и влияние критерия 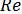 на инерционное осаждение. При ламинарном течении потока (Re=υгℓρг/ /μг<2) эффективность осаждения не будет зависеть от этого критерия пока можно пренебречь существованием пограничного слоя вокруг обтекаемого тела (вязкое обтекание). С увеличением значения критерия
на инерционное осаждение. При ламинарном течении потока (Re=υгℓρг/ /μг<2) эффективность осаждения не будет зависеть от этого критерия пока можно пренебречь существованием пограничного слоя вокруг обтекаемого тела (вязкое обтекание). С увеличением значения критерия 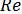 при перехода к турбулентному движению потока на поверхности обтекаемого тела образуется пограничный слой, толщина которого уменьшается по мере роста критерия
при перехода к турбулентному движению потока на поверхности обтекаемого тела образуется пограничный слой, толщина которого уменьшается по мере роста критерия 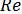 . При значениях
. При значениях 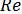 больше критического (Re>500) линии тока сильнее изгибаются (потенциальное обтекание)и обтекают тело на более близком от него расстоянии, вследствие чего при том же значении критерия
больше критического (Re>500) линии тока сильнее изгибаются (потенциальное обтекание)и обтекают тело на более близком от него расстоянии, вследствие чего при том же значении критерия 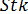 эффективность осаждения будет выше. Этот рост эффективности будет продолжаться с уменьшением толщины пограничного (ламинарного) слоя вокруг тела, т. е. с увеличением критерия
эффективность осаждения будет выше. Этот рост эффективности будет продолжаться с уменьшением толщины пограничного (ламинарного) слоя вокруг тела, т. е. с увеличением критерия 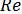 . Таким образом, при потенциальном обтекании эффективность осаждения зависит как от критерия
. Таким образом, при потенциальном обтекании эффективность осаждения зависит как от критерия 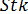 , так и от критерия
, так и от критерия 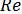 .
.
Рисунок2.5 - Осаждение частиц на шаре:
-движение газов; ------------движение частиц.
Еще более сложный характер приобретает пограничный слой при развитом турбулентном течении потока. Поэтому целесообразно рассматривать только системы с одинаковым значением критерия 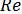 или системы, в которых режим движения потока приближается к автомодельному, и критерий
или системы, в которых режим движения потока приближается к автомодельному, и критерий 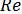 можно не учитывать при расчетах.
можно не учитывать при расчетах.
Ниже приводится ряд диаграмм и эмпирических формул, позволяющих рассчитать значения 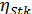 . При получении этих формул предполагалось, что инерционное осаждение частиц происходит на стороне тела, обращенной навстречу потоку, т. е. не учитывалось влияние завихрения на подветренной стороне тела, которое также может способствовать осаждению частиц.
. При получении этих формул предполагалось, что инерционное осаждение частиц происходит на стороне тела, обращенной навстречу потоку, т. е. не учитывалось влияние завихрения на подветренной стороне тела, которое также может способствовать осаждению частиц.
В области 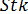 ≥ 1 при потенциальном обтекании коэффициент осаждения на шаре может быть определен по эмпирической формуле [3]
≥ 1 при потенциальном обтекании коэффициент осаждения на шаре может быть определен по эмпирической формуле [3]

Величина 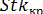 (в качестве определяющего линейного параметра в критерии
(в качестве определяющего линейного параметра в критерии 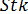 принят диаметр шара
принят диаметр шара 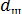 ), соответствующая
), соответствующая 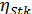 = 0 составляет 0,0417. При выводе формулы (2.30) было принято, что идеальный поток движется вдоль поверхности тела, т. е. совершенно не учитывалось существование пограничного слоя.
= 0 составляет 0,0417. При выводе формулы (2.30) было принято, что идеальный поток движется вдоль поверхности тела, т. е. совершенно не учитывалось существование пограничного слоя.
Путем аналитического решения уравнения (2.28) при потенциальном обтекании шара вблизи точки на бегания потока было получено [7] близкое значение критерия 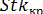 = 1/24.
= 1/24.
1 - по теоретическим данным; 2 - по экспериментальным данным.
Рисунок 2.6 - Инерционное осаждение частиц на шаре при потенциальном его обтекании.
На рис. 2.5 приведены теоретические и экспериментальные зависимости эффективности осаждения частиц на шаре при потенциальном его обтекании. Данные, приведенные на рис. 2.6, могут быть использованы и при практических расчетах эффективности пылеулавливающих установок, в которых осаждение осуществляется на телах шарообразной формы (например, на капле). При этом, если тела расположены не очень тесно, заметного искажения потока не будет. При тесном расположении обтекаемых тел эффективность может увеличиваться по сравнению с теоретической величиной ηStk для одиночного тела, что объясняется более близким прохождением линий токов.
На рис. 2.7 приведены значения ηStk при потенциальном обтекании цилиндра для различных отношений 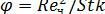 . Величина
. Величина 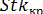 в этом случае равна 1/16.
в этом случае равна 1/16.
Рисунок2.7 - Инерционное осаждение частиц при потенциальном обтекании цилиндра при различных значениях 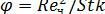 : 1 - φ = 0; 2 - φ=100; 3 - φ=1·103; 4 - φ=1·104; 5 - φ=5·104.
: 1 - φ = 0; 2 - φ=100; 3 - φ=1·103; 4 - φ=1·104; 5 - φ=5·104.
Практика показывает, что функция ηStk =f(Re, Stk) является нормально-логарифмической. Поэтому на графике с вероятностно-логарифмической шкалой ординат в определенном гидродинамическом режиме ( 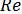 = const) она может быть изображена в виде прямой линии.
= const) она может быть изображена в виде прямой линии.
В переходной области обтекания цилиндра (0,2< 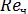 < 150) прямая для инерционного осаждения частиц на цилиндре описывается уравнением
< 150) прямая для инерционного осаждения частиц на цилиндре описывается уравнением
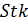 0,5= l,253
0,5= l,253 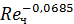 (2.31)
(2.31)
Дата добавления: 2016-01-18; просмотров: 1215;
