Статические моменты плоских сечений

Площадь стержня.

При расчетах элементов конструкций используются различные геометрические характеристики. Так, например, при растяжении и сжатии используется площадь поперечного сечения стержня. Она применяется при определении напряжений и деформаций растянутого или сжатого стержня, т.е. чем больше площадь поперечного сечения тем большую нагрузку сможет выдержать стержень.

Оказывается, при других деформациях эта геометрическая характеристика не является достаточной. Необходимо использовать другие, более сложные геометрические характеристики.

Статические моменты плоских сечений

Нетрудно убедиться, что в случае изгиба бруса площадь се­чения не может служить характеристикой его жесткости. Дей­ствительно, из двух брусьев (рис. 2.2.1) с равновеликими площа­дями поперечных сечений первый при данной нагрузке деформируется значительно сильнее второго (например, при h/b = 2 прогибы первого бруса в четыре раза больше, чем второго).

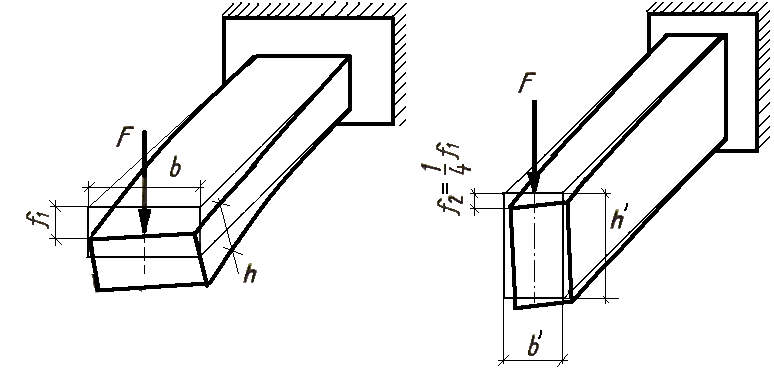
Рисунок 2.2.1

Следовательно, при одной и той же площади поперечного сечения стержня, но при разном расположении его стержень сопротивляется изгибу по разному. Это позволяет сделать вывод о том, что площадь поперечного сечения не может характеризовать сопротивляемость стержня изгибу и при изучении изгиба приходится вводить другие геометрические характеристики — статический момент площади (сечения).

Выполняя расчеты на прочность, необходимо бывает вычислять статические моменты всего сечения или части его относительно некоторых осей.

Рассмотрим произвольное поперечное сечение стержня в системе координат х,у, выдел элементарную площадку dА (рис. 2.2.2)

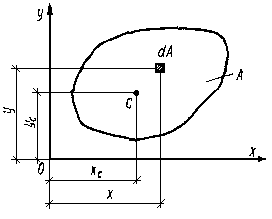
Рисунок 2.2.2

Статическим моментом сечения относительно данной оси называется сумма произведений элементарных площадей dА, на их расстояния до данной оси (например, х или у), которая распространяется на всю площадь сечения А.

Так, статические моменты сечения относительно осей х и у равны:

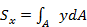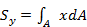; (2.2.1)

Статические моменты обычно выражаются в см³ или м³. При параллельном переносе осей значения статических моментов не остаются постоянными, а изменяются и могут иметь как положительное, так и отрицательное значение. Следовательно, среди семейства параллельных осей существует единственная ось, относительно которой статический момент равен нулю

Ось, относительно которой статический момент равен нулю, называется центральной.

Точка пересечения центральных осей называется центром тяжести сечения.

Можно показать, что и относительно любой оси, проходящей через центр тяжести сечения, статический момент равен нулю. Для изображенного на рис. 2.2.2 сечения центр тяжести располагается в точке С, его координатами являются ординаты х_с и у_с. Все оси, которые проходят через эту точку, будут центральными и относительно таких осей статический момент равен нулю.

На основании теоремы Вариньона следует, что

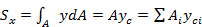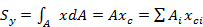; (2.2.2)

Следовательно, статический момент площади А относительно какой-либо оси равен произведению всей площади на расстояние от ее центра тяжести до этой оси.

Из выражений (2.2.2) получим формулы для определения координат центра тяжести сечения:

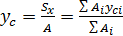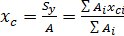; (2.2.3)

Заметим, что последняя форма записи в выражениях (2.2.3) относится к определению координат центра тяжести сложного сечения разбитого на простейшие составные части, для которых известны площади А и положение центра тяжести и у_с

Для большинства сечений определение положения центра тяжести упрощается. Так, если сечения имеют ось или центр симметрии, то центр тяжести в таких сечениях находится соответственно на оси симметрии или в центре симметрии.