Способ моментных точек.

Главнейшая задача статики ферм заключается применении таких способов расчета, которые избавляют от решения системы совместных уравнений.

Способ моментных точек в наиболее простой форме применяется к фермам, в которых можно провести разрез только через три стержня.

Определение усилия O₂, D₂, U₂ в элементах фермы с треугольной решеткой (рис.1.4.1). Предварительно находим о реакции А и В. Проводим разрез п-п через три стержня усилия в которых определяются, и действия частей фермы представляем соответствующим векторами O₂, D₂, U₂ полагая усилия растягивающими.

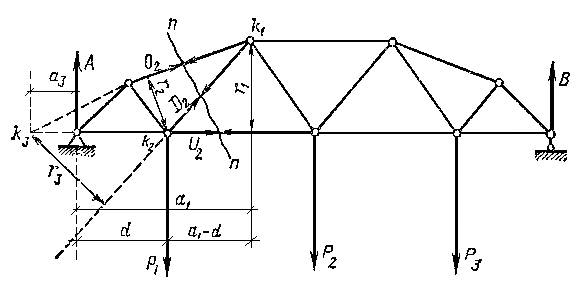
Рисунок 1.4.1.

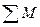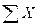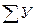Рассматривая равновесие левой части (где меньше сил), составляем три уравнения, каждое из которых включает только одно неизвестное. Для этого вместо трех классических уравнений: = 0, =0, =0 получим для левой отсеченной части уравнения следующего вида:

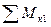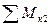=0; =0; 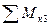=0; (1.4.1)

где в сумму моментов 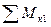не войдут усилия O₂, D₂ проходящие через моментную точку к₁. Сумма моментов 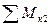не содержит усилий D₂, U_2; сумма 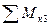не включает усилий O₂,U₂ . Каждое уравнение (1.4.1) будет содержать только одно неизвестное усилие, что позволит легко и точно его найти. Для определения U₂, составляем сумму моментов сил, приложенных к отсеченной левой части фермы, относительно точки пересечения направлений усилий O₂, D₂:

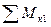=0;

или Аа₁-Р₁(а₁-d) – U₂ r ₁=0

откуда U₂ = [Aa₁ — P₁(а₁-d)]/ r ₁

Здесь числитель не что иное, как момент левых внешних сил относительно точки к₁ (изгибающий момент в сечении воображаемой балки со сплошной стенкой).

Таким образом, получаем U₂ = М_{вн к1}/ r ₁

,где М_{вн к1} – момент левых внешних сил относительно точки к₁;

r ₁— плечо усилия.

Найдем теперь усилие O₂ составляю сумму моментов сил, приложенных к левой отсеченной части фермы, относительно точки к₂ - точки схода D₂, U₂:

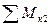=0

или Аd + O₂ r₂=0

откуда O₂= — Аd / r₂ = —М_{вн к2} / r₂

Для определения усилия D₂ выбираем точку моментов к₃ — точке пересечения направлений усилий O₂, U₂ .Рассматривая равновесие левой части, находим

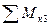=0;

или -Аa₃, + Р, (d+a₃) — D₂r₃ =0,

откуда D₂ = [ Р (d+a₃) -Аa₃]/ r₃

Как видим, при применении способа моментных точек усилие всегда выражается отношением момента внешних сил, приложенных к левой отсеченной части, к плечу усилия.

Так, для определения усилия U₂ в элементе нижнего пояса полураскосной фермы (рис. 1.4.2) проводим разрез п — п, пересекающий четыре стержня.

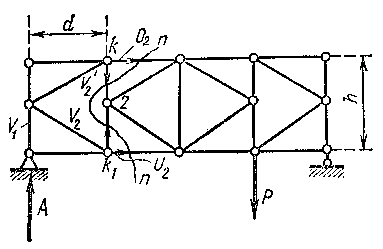
Рисунок 1.4.2

Но направления трех усилий O₂, V₂ и V₂¹ пересекаются в одной точке. Ее и принимаем за точку моментов для определения U₂:

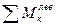=0

откуда Ad – U₂h=0; U₂= Ad/ h.

Аналогично определяется усилие О₂ с использованием моментной точки к₁.

Замкнутый разрез применяем для отыскания усилий в стернях фермы Шухова (рис. 1.4.3) и подобных ей системах. Положим, требуется определить усилие О₁, в первом элементе верхнего пояса фермы Шухова.

Для определен усилий в стержнях О₁, О₂, и О₅ связывающих два основных треугольника, проводим разрез, который рассекает стержни верхнего пояса по одному разу и раскосы D₁ и D₂ по два раза.

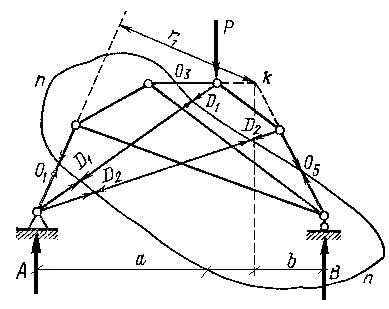
Рисунок 1.4.3

Рассматривая равновесие части фермы расположенной внутри разреза п—п, составляем условие равновесия в виде равенства нулю суммы моментов относительно к— точки пересечении осевых линий стержней О₂ и О₅:

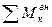=0

или -O₁r₁ – Bb = 0

откуда О₁ = -Bb/ r₁

Способ проекций.

Способ проекций применяют когда моментная точка оказывается в бесконечности, т. е. при параллельности двух стержней из трех рассеченных. Допустим требуется определить усилие в раскосе D₃ фермы с параллельными поясами (рис. 1.4.4).

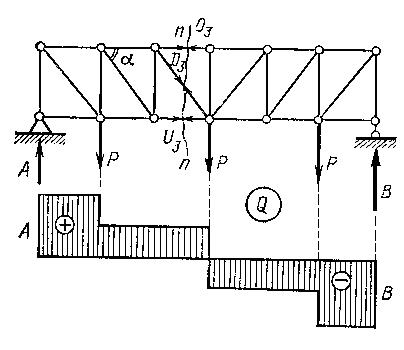
Рисунок 1.4.4.

Проводя разрез п-п, рассекаем три стержня, усилия в которых O₃, D₃, U_3. Направления усилий O₃ и U₃, параллельны, следовательно моментная точка для D₃ будет в бесконечности. Задача определения усилия D₃ легко решается применением уравнения проекций всех сил, приложенных к отсеченной части, на вертикальную ось, перпендикулярную направлениям O₃ и U_3:

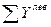=0

или: А-Р-D₃sin 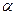= 0

откуда D₃ = (A— Р)/ sin 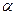= Q_пп/ sin ,

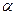где (А-Р)= Q_пп – поперечная сила в сечении п—п воображаемой балки со сплошной стенкой.

Раскос фермы с параллельными поясами работает на восприятие поперечной силы. Закон изменения усилий в раскосах легко установить по эпюре поперечных сил.

1.4.3 Способ вырезания узлов.

Способ вырезания узлов наряду со способом моментов является одним из самых общих способов определения усилий. Для каждого узла фермы составляют два условии равновесия в виде двух уравнений проекций на две непараллельные оси. Целесообразно поэтому начинать с узла, где сходятся два

стержня. Покажем применение способа вырезания узлов для определения усилий в элементах фермы, представленной на рис. 1.4.5, а. Для определения усилия О проще всего вырезать опорный узел фермы (рис. 1.4.5,6).

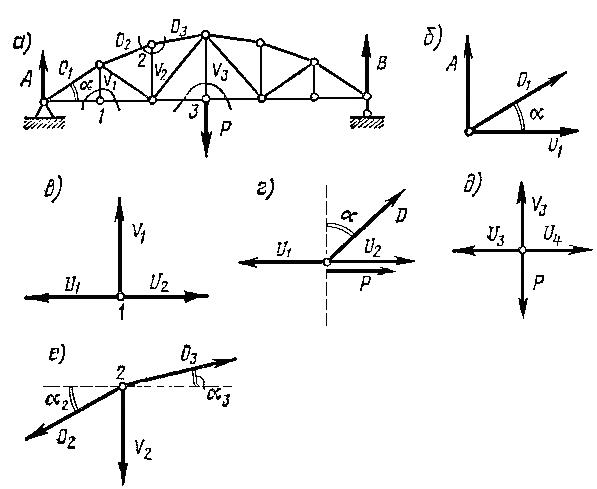
Рисунок 1.4.5

Проектируя все силы, действующие на узел, на вертикаль получаем:

O₁ sin 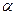+ A = 0

Откуда O₁= - A/ sin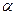

т. е. усилие в опорном элементе верхнего пояса фермы пропорционально опорной реакции.

Для определения усилий в стойках V₁ и V₂ вырезаем соответственно узлы 1 и З нижнего пояса фермы. и проектируя все силы, приложенные к нему на вертикальную ось, получаем (рис. 1.4.5, в) V₁ = 0. Отсюда можно сделать следующее заключение: если в узле сходятся три стержня, из которых два направлены одинаково(U₁ и U₂)и нет нагрузки, то усилие в отдельно направленном стержне(V₁)равно нулю. Такой стержень называют нулевым. Указанное правило распространяется также на узлы, к которым приложена нагрузка, не имеющая составляющей, нормальной к двум другим стержням одного и того же направления.

Предположим, что к узлу, в котором сходятся два поясных усилия U₁ и U₂ и усилие в раскосе D, приложена горизонтальная сила Р (рис. 1.4.5,г). Проектируя все силы, действующие на узел, на вертикаль, находим:

D cos 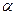= 0.

откуда D = 0.