НЕСИММЕТРИЧНЫЕ ТРЁХФАЗНЫЕ ЦЕПИ
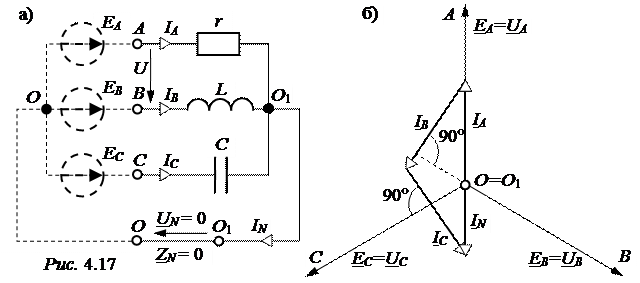
ЗАДАЧА 4.14. Определить токи в четырёхпроводной цепи (рис. 4.17,а) и напряжения на фазах несимметричного приёмника, включенного в симметричную трёхфазную сеть с напряжением U = 380 B, если
r = wL = 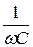 = 44 Ом.
= 44 Ом.
Найти активную и реактивную мощности несимметричного приёмника, построить векторную диаграмму.
Решение
По умолчанию считаем, что фазы симметричного генератора соединены в звезду с выведенной нулевой точкой О (на рис. 4.17,а показано штриховыми линиями). Так как сопротивление нулевого провода ZN = 0, то потенциалы j 0 = j 01 = 0 и UN = j 0 – j 01 = 0.
В этом случае фазные напряжения несимметричного приёмника равны фазным ЭДС симметричного генератора UA = EA – UN = EA, аналогично UB = EB, UС = EС.
Фазная ЭДС E = 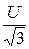 =
= 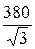 = 220 В.
= 220 В.
Приняв EA = 220 В, получим ЕB = 220×e -j120° B, ЕС = 220×e j120° B.
По закону Ома токи
IA =  =
= 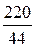 = 5 А; IВ =
= 5 А; IВ =  =
= 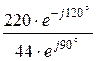 = 5×e –j210° А;
= 5×e –j210° А;
IС = 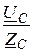 =
= 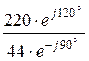 = 5×e j210° А, а по первому закону Кирхгофа
= 5×e j210° А, а по первому закону Кирхгофа
IN = IA + IВ + IС = 5×(1 + e –j210° + e j210°) = 5×(1 - 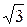 ) = -3,64 A.
) = -3,64 A.
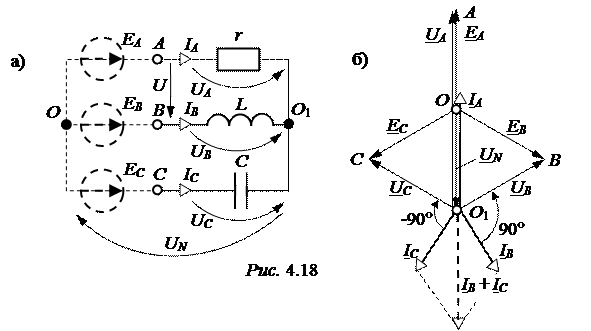
Векторная диаграмма цепи приведена на рис. 4.17,б.
Активная мощность приёмника
Р = РА + РВ + РС = 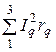 = IA2×r = 52×44 = 1100 Вт.
= IA2×r = 52×44 = 1100 Вт.
Реактивная мощность также определяется как алгебраическая сумма мощностей трёх фаз приёмника
Q = QА + QВ + QС = 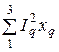 = IB2×wL - IC2×
= IB2×wL - IC2× 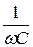 = 52×44 - 52×44 = 0.
= 52×44 - 52×44 = 0.
 ЗАДАЧА 4.15. Решить задачу 4.14 при разомкнутом нулевом проводе.
ЗАДАЧА 4.15. Решить задачу 4.14 при разомкнутом нулевом проводе.
Решение
Приведём расчётную схему установки (рис. 4.18,а).
Рассчитаем узловое напряжение (напряжение смещения нейтрали)
UN = 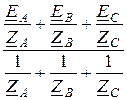 = 220×(1 + e –j210° + e j210°) = -160 B.
= 220×(1 + e –j210° + e j210°) = -160 B.
Фазные напряжения приёмника
UA = EA – UN = 220 + 160 = 380 B, UA = 380 B;
UB = EB – UN = 220×e –j120° + 160 = 50– j190 B, UB = 196,5 B;
UC = EC – UN = 220×e j120° + 160 = 50+ j190 B, UC = 196,5 B.
Фазные токи приёмника равны линейным
IA =  =
= 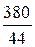 = 8,64 A, IA = 8,64 A;
= 8,64 A, IA = 8,64 A;
IB = 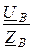 =
= 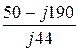 = -4,32 – j1,14 A, IB = 4,47 A;
= -4,32 – j1,14 A, IB = 4,47 A;
IC = 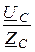 =
= 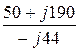 = -4,32 + j1,14 A, IC = 4,47 A.
= -4,32 + j1,14 A, IC = 4,47 A.
Проверка осуществляется по I закону Кирхгофа: IA + IВ + IС = 0, то есть выполняется.
Активная мощность приёмника
Р = 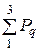 = IA2×r = 8,642×44 = 3285 Вт.
= IA2×r = 8,642×44 = 3285 Вт.
Реактивная мощность
Q =  = IB2×wL - IC2×
= IB2×wL - IC2× 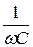 = 4,472×44 – 4,472×44 = 0.
= 4,472×44 – 4,472×44 = 0.
ЗАДАЧА4.16. Рассчитать токи несимметричного треугольника (рис. 4.19,а), построить векторную диаграмму, если
U = 380 В, r = xC = 100 Ом, xL = 100 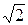 Ом.
Ом.
 |
Найти показания ваттметров, сравнить их с активной мощностью несимметричного трёхфазного приёмника.
Решение
При подключении треугольника сопротивлений к трёхфазному генератору линейные напряжения генератора равны фазным напряжениям нагрузки. Примем UAB = 380 B = UAX, тогда
UBY = UBC = 380×e -j120° B, UCZ = UСA = 380×e j120° B.
По закону Ома находим фазные токи треугольника
Iax =  =
=  = 3,8 А; Iby =
= 3,8 А; Iby = 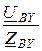 =
= 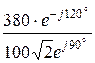 = 1,9
= 1,9 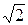 ×e –j210° А;
×e –j210° А;
Icz =  =
= 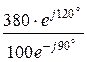 = 3,8×e j210° А.
= 3,8×e j210° А.
Линейные токи находим по I закону Кирхгофа
IA = Iax – Icz = 3,8 – 3,8×e j210° = 3,8 + 3,3 + j1,9 = 7,1 + j1,9 = 7,35×e j15° А;
IВ = Iby – Iax = -2,3 + j1,34 – 3,8 = -6,13 + j1,34 = -6,28×e –j12,33° А;
IС = Icz – Iby = -3,3 – j1,9 + 2,33 – j1,34 = -0,97 – j3,24 = -3,38×e j73,33° А.
Векторная диаграмма треугольника сопротивлений приведена на рис. 4.19,б.
Показания ваттметров
PW1 = Re[UAB×  ] = Re[380×(7,1 – j1,9)] = 2698 Вт,
] = Re[380×(7,1 – j1,9)] = 2698 Вт,
PW2 = Re[UСB× 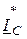 ] = Re[-380×e –j120°×(-3,38×e -j73,33°)] = -1250 Вт.
] = Re[-380×e –j120°×(-3,38×e -j73,33°)] = -1250 Вт.
Активная мощность несимметричного приёмника
Р = РАХ + РВY + РСZ = Iах2×r = 3,82×100 = 1444 Вт.
Сумма показаний двух ваттметров схемы рис. 4.19,а
PW1 + PW2 = 2698 – 1250 = 1448 Вт = Р.
Таким образом, приведенная схема включения двух ваттметров есть схема измерения активной мощности в трёхфазной трёхпроводной цепи, а отличие в четвёртом знаке результатов есть следствие округления чисел.
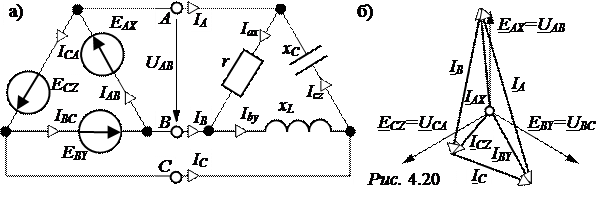
ЗАДАЧА 4.17. Схема задачи 4.16 питается от симметричного источни-ка, фазы которого соединены в треугольник. Считая источник питания идеаль-ным (рис. 4.20,а), фазную ЭДС ЕАХ = 380 B, найти фазные токи генератора.
 |
Решение
Так как внутренние сопротивления фаз трёхфазного источника питания равны нулю, то при любых токах нагрузки линейные напряжения
UAВ = ЕАХ = 380 B, UВС = ЕВY = 380×e –j120° B, UСА = ЕСZ = 380×e j120° B;
что совпадает с линейными напряжениями схемы задачи 4.16, на основании расчётов которой линейные токи
IA = 7,1 + j1,9 А; IВ = -6,13 + j1,34 А; IС = -0,97 – j3,24 А.
Для расчёта фазных токов генератора составим систему уравнений Кирхгофа. По первому закону Кирхгофа для узлов
А) iАВ – iСА = iА; В) iВС – iАВ = iВ.
Уравнение по второму закону Кирхгофа для контура, состоящего из фаз генератора, запишем, исходя из того, что внутреннее сопротивление фазы генератора Z любое, но для всех фаз одинаковое – симметричный генератор. Получим iАВ×Z + iВС×Z + iСА×Z = ЕАХ + ЕBY + ЕCZ.
У симметричного генератора ЕАХ + ЕBY + ЕCZ º 0, поэтому
Z×(iАВ + iВС + iСА) º 0 при любом внутреннем сопротивлении Z.
Таким образом, для расчёта фазных токов источника питания необходимо решить систему уравнений
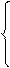 iАВ – iСА = iА;
iАВ – iСА = iА;
iВС – iАВ = iВ;
iАВ + iВС + iСА = 0;
откуда с учётом iА + iВ + iС = 0 получаем:
iАВ =  ; iВС =
; iВС = 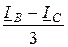 ; iСА =
; iСА = 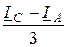 .
.
Для рассматриваемого примера получаем:
iАВ = 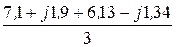 = 4,41 + j0,19 А, iАВ =4,41 А;
= 4,41 + j0,19 А, iАВ =4,41 А;
iВС = 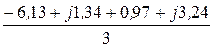 = -1,71 + j1,53 А, iВС =2,3 А;
= -1,71 + j1,53 А, iВС =2,3 А;
iСА = 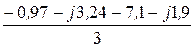 = -2,69 – j1,71 А, iСА =3,19 А.
= -2,69 – j1,71 А, iСА =3,19 А.
Отметим, что фазные токи источника питания отличаются от фазных токов нагрузки, для которой на основании задачи 4.16 получено:
Iax = 3,8 А; Iby = 2,7 А; Icz = 3,8 А.
Векторная диаграмма токов источника питания приведена на рис.4.20,б.
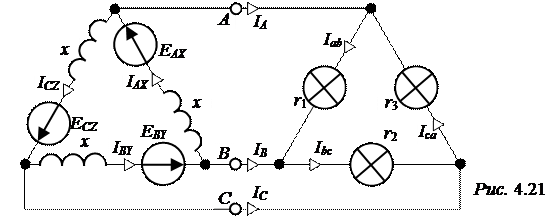 |
ЗАДАЧА4.18. Для питания осветительной нагрузки в опасных средах (угольная пыль и метан шахт, мукомольная пыль мельниц, цехи, обрабатывающие дерево, лакокрасочные производства и т.п.) применяется система треугольник-треугольник (рис. 4.21).
Генератор симметричный, его фазные ЭДС ЕАХ = EВY = EСZ = 127 B, внутреннее сопротивление фазы x = 9 Ом. Нагрузка неравномерная, причём r1 = 20 Ом, r2 = 30 Ом, r3 = 50 Ом. Рассчитать состояние цепи.
 Решение
Решение
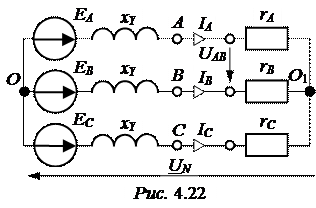
Преобразуем активный трёх-полюсник в эквивалентную звезду (рис. 4.22):
ЕА = EВ = EС =  =
= 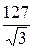 = 73,3 B,
= 73,3 B,
xY = 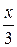 =
= 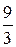 = 3 Ом.
= 3 Ом.
Так же поступим и с нагрузкой. Сопротивления эквивалентной звезды
rA = 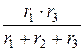 =
=  = 10 Ом;
= 10 Ом;
rВ = 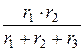 =
= 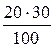 = 6 Ом; rС =
= 6 Ом; rС = 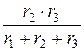 =
= 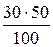 = 15 Ом.
= 15 Ом.
Примем ЕА = 73,3 B, тогда ЕВ = 73,3×e –j120° B, ЕС = 73,3×e j120° B.
Узловое напряжение
UN = 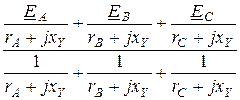 =
= 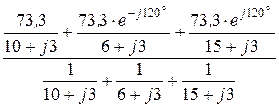 =
=
= -17,05×e j61,99°= -8 – j15,05 B.
Линейные токи
IА = 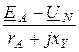 =
= 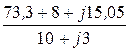 = 7,87 – j0,857 A;
= 7,87 – j0,857 A;
IB = 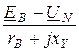 =
= 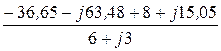 = -7,047 – j4,545 A;
= -7,047 – j4,545 A;
IC = 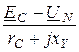 =
= 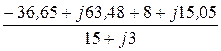 = -0,829 + j5,397 A.
= -0,829 + j5,397 A.
Линейное напряжение на нагрузке
UAB = IА×rA – IB×rB = (7,87 – j0,857)×10 – (-7,047 – j4,545)×6 =
= 121 + j18,7 = 122,4×e j8,79° B.
Фазные токи осветительной нагрузки (рис. 4.21)
Iab = 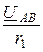 =
= 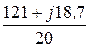 = 6,05 + j0,935 = 6,122×e j8,79° A;
= 6,05 + j0,935 = 6,122×e j8,79° A;
Ica = Iab – IА = 6,05 + j0,935 – 7,87 + j0,857 = -1,82 + j1,792 = 2,554×e j135,44° A;
Ibc = Iab + IB = 6,05 + j0,935 – 7,047 – j4,545 = -0,997 – j3,61 = 3,745×e -j105,44° A.
Линейные напряжения
UBC = Ibc ×r2 = 112,4 B, UCA = Ica ×r3 = 127,7 B.
Активная мощность осветительной нагрузки и генератора
P = PАB + PBC + PCA = Iab2×r1 + Ibc2×r2 + Ica2×r3 =
= 6,1222×10 + 3,7452×30 + 2,5542×50 = 1122 Вт = 1,122 кВт.
Фазные токи источника питания (см. задачу 4.17)
iАХ =  = 4,972 + j1,229 = 5,122×e j13,88° A;
= 4,972 + j1,229 = 5,122×e j13,88° A;
iВY = 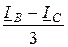 = -2,073 – j3,314 = -3,91×e j57,97° A;
= -2,073 – j3,314 = -3,91×e j57,97° A;
iСZ = 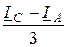 = -2,9 + j2,085 = -3,572×e -j35,71° A.
= -2,9 + j2,085 = -3,572×e -j35,71° A.
Реактивная мощность генератора (и всей цепи)
Q = QАX + QBY + QCZ = IАX2×x + IBY2×x + ICZ2×x =
= 9×(5,1222 + 3,912 + 3,5722) = 488,5 вар = 0,4885 квар.
Полная мощность источника питания
S = 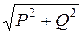 =
= 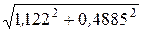 = 1,224 кВA.
= 1,224 кВA.
Коэффициент мощности источника питания cosj = 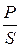 =
= 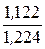 = 0,917.
= 0,917.
ЗАДАЧА 4.19. Трёхфазная цепь (рис. 4.23) подключена к симметрич-ному генератору с напряжением U = 660 B. Параметры цепи
r = wL = 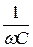 = 10 Ом, r1 = wL1= 5 Ом.
= 10 Ом, r1 = wL1= 5 Ом.
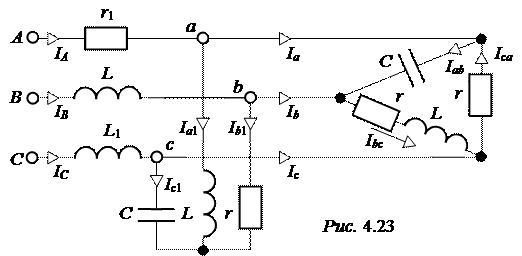 |
Рассчитать линейные и фазные токи всех участков цепи.
Дата добавления: 2016-01-18; просмотров: 3707;
