Средние показатели динамики
| № п/п | Показатель | Метод расчета |
| 1. | Средний уровень ряда ( 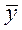 ):
- для интервального ряда
- для моментного ряда
с равными интервалами
с неравными интервалами ):
- для интервального ряда
- для моментного ряда
с равными интервалами
с неравными интервалами
|

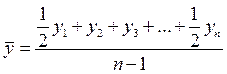
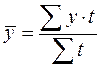
|
| 2. | Средний абсолютный прирост (  ): ):
| 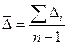 или или 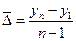
|
| 3. | Средний коэффициент роста ( 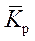 ): ):
| 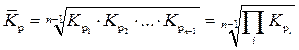 или
или 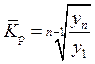
|
| 4. | Средний темп роста ( 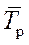 ),% ),%
| 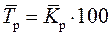
|
| 5. | Средний темп прироста ( 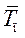 ), % ), %
| 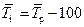
|
| 6. | Средняя величина абсолютного значения 1 % прироста ( 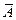 ) )
| 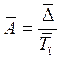
|
Хронологическая средняя – средняя, исчисляемая из уровней динамического ряда.
Средняя хронологическая интервального ряда исчисляется по формуле средней арифметической, причем при равных интервалах применяется средняя арифметическая простая, а при неравных – средняя арифметическая взвешенная.
Средняя хронологическая моментного ряда исчисляется как сумма всех уровней ряда, поделенного на число членов ряда без одного, причем первый и последний члены ряда берутся в половинном размере.
Средний абсолютный прирост – показатель, характеризующий среднюю абсолютную скорость роста (или снижения) уровня за отдельные периоды времени. Он показывает, на сколько единиц увеличился (или уменьшился) уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежемесячно и т.д.).
Средний темп роста – относительный показатель, выраженный в форме коэффициента и показывающий, во сколько раз увеличился уровень по сравнению с предыдущим, во сколько раз увеличился уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежеквартально и т.п.).
Средний темп прироста – относительный показатель, выраженный в процентах и показывающий, на сколько увеличился (или уменьшился) уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежемесячно и т.п.).
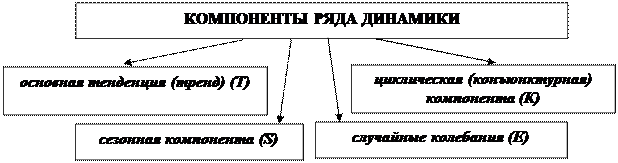
Рис. 4.5. Компонентная структура ряда динамики
Основная тенденция (тренд) – достаточно плавное и устойчивое изменение уровня явления во времени, более или менее свободное от случайных колебаний. Основная тенденция складывается под влиянием факторов эволюционного характера, и ее можно представить либо аналитически, в виде уравнения (модели) тренда, либо графически.
Циклические колебания в экономических процессах примерно соответствуют так называемым циклам конъюнктуры. Они складываются под влиянием факторов осциллятивного характера и могут быть описаны с помощью модели синусоидальной кривой 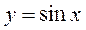 .
.
Сезонные колебания – это колебания периодически повторяющиеся в некоторое определенное время каждого года, дня месяца или часа дня, они формируются также под воздействием факторов осциллятивного характера.
Случайные (нерегулярные) колебания в социально-экономических явлениях могут быть вызваны: а) спорадически наступающими изменениями (война, эпидемия, экологическая катастрофа и т.д.); б) совокупностью случайных колебаний, являющихся результатом действия большого количества относительно слабых второстепенных факторов.

Рис. 4.6. Типизация моделей рядов динамики
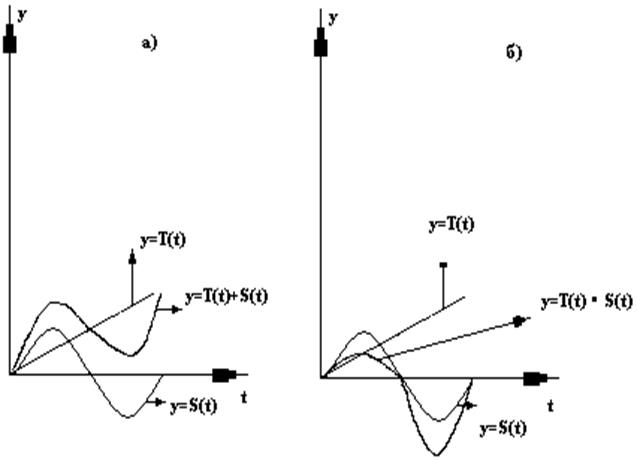
Рис. 4.7. Сочетание различных составляющих ряда динамики:
а) при аддитивной связи; б) при мультипликативной связи.
 |
Рис. 4.8 Классификация методов сглаживания ряда динамики


Рис. 4.9 Классификация уравнений трендов, отображающих развитие социально-экономических явлений во времени
Согласноправилу выбора степени полинома модели развития, основанному на определении величин конечных разностей уровней динамических рядов, полином 1-й степени применяется как модель такого ряда динамики, у которого первые разности (абсолютные приросты) постоянны; полиномы 2-й степени – для отражения ряда динамики с постоянными вторыми разностями (ускорениями); полиномы 3-й степени - с постоянными третьими разностями и т.д. Признаком экспоненциального тренда является тенденция развития абсолютных цепных приростов.
Гармонический анализ представляет собой операцию по выражению заданной периодической функции в виде ряда Фурье по гармоникам разных порядков 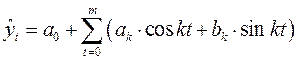 , откуда
, откуда 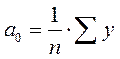 ;
; 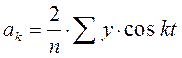 и
и 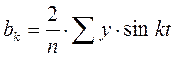 .
.
Сезонная компонента ряда динамики – внутригодичные колебания, имеющие более или менее регулярный характер. Их мерой обычно является индекс сезонности.
Сезонные колебания характеризуются специальными показателями, которые называют индексами сезонности ( 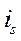 ):
):
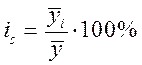 ,
,
где 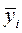 - средняя величина одного и того же уровня (месяца)
- средняя величина одного и того же уровня (месяца)
в течение различных периодов (лет);
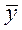 - средняя величина уровня для всего ряда.
- средняя величина уровня для всего ряда.
Если ряд динамики содержит определенную тенденцию в развитии, то прежде чем вычислить сезонную волну фактические данные нужно обработать так, чтобы выявить общую тенденцию, т.е. прибегают к аналитическому выравниванию ряда динамики. С этой целью:
- по соответствующему полиному вычисляют для каждого месяца (квартала) выравненные (теоретические) уровни на момент времени 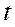 ;
;
- определяют отношение фактических месячных (квартальных) данных 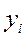 к соответствующим выравненным данным
к соответствующим выравненным данным 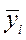 в процентах, т.е.
в процентах, т.е. 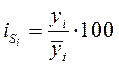 ;
;
- находят средние арифметические из процентных соотношений, рассчитанных по одноименным периодам в процентах, т.е. 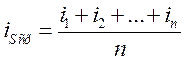 .
.
Исследование динамики социально-экономических явлений, выявление и характеристика основной тенденции развития и моделей взаимосвязи дают основание для прогнозирования – определения будущих размеров уровня социально-экономического явления.
Интерполяция – приближенный расчет уровней, лежащих внутри ряда динамики, но почему-либо неизвестных.
Лаг – промежуток времени отставания одного явления на другого, связанного с ним.
Экстраполяция – нахождение уровней за пределами изучаемого ряда, т.е. продление ряда на основе выявленной закономерности изменения уровней в изучаемый отрезок времени. Экстраполяция, проводимая в будущее, называется перспективной и в прошлое – ретроспективой. Экстраполяцию в общем виде можно представить формулой:
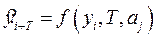 ,
,
где 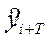 - прогнозируемый уровень;
- прогнозируемый уровень;
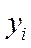 - текущий уровень прогнозируемого ряда;
- текущий уровень прогнозируемого ряда;
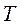 - период упреждения;
- период упреждения;
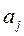 - параметр уравнения тренда.
- параметр уравнения тренда.
Прогнозирование по среднему абсолютному приросту может быть выполнено в том случае, если выполняется предположение о равномерном изменении ряда (абсолютный прирост стабилен),
т.е.  ,
,
где 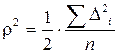 и
и 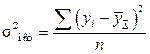 .
.
В этом случае экстраполяцию можно выполнить по формуле:
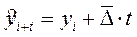 ,
,
где 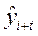 - экстраполируемый уровень, а (
- экстраполируемый уровень, а ( 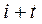 ) – номер этого уровня;
) – номер этого уровня;
 - номер последнего уровня исследуемого периода, за который рассчитан
- номер последнего уровня исследуемого периода, за который рассчитан 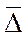 ;
;
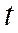 - срок прогноза (период упреждения);
- срок прогноза (период упреждения);
 - средний абсолютный прирост.
- средний абсолютный прирост.
Любой статистический прогноз носит приближенный характер. Поэтому целесообразно определение доверительных интервалов прогноза. Величина доверительного интервала определяется следующим образом:
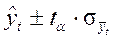 ,
,
где 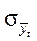 - средняя квадратическая ошибка тренда;
- средняя квадратическая ошибка тренда;
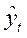 - расчетное значение уровня;
- расчетное значение уровня;
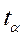 - доверительная величина.
- доверительная величина.
При изучении развития явления во времени часто возникает необходимость оценить степень взаимосвязи в изменениях уровней двух и более рядов динамики различного содержания, но связанных между собой.

Рис. 4.10. Классификация методов изучения корреляции рядов динамики
Расчет парного коэффициента корреляции по уровням ряда динамики осуществляют по формуле:
 ,
,
где 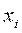 - уровни первого ряда динамики;
- уровни первого ряда динамики;
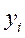 - уровни второго ряда динамики.
- уровни второго ряда динамики.
Расчет парного коэффициента корреляции по отклонениям фактических уровней от выравненных по уравнению (тренду)осуществляется по формуле:
 ,
,
где  и
и 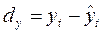 - отклонения эмпирических уровней от выравненных уровней двух рядов динамики.
- отклонения эмпирических уровней от выравненных уровней двух рядов динамики.
Расчет парного коэффициента корреляции по абсолютным отклонениям уровней ряда динамики осуществляется по формуле:
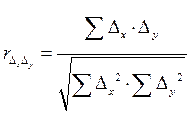 ,
,
где 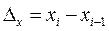 и
и 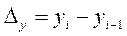 - разности уровней рядов динамики.
- разности уровней рядов динамики.
Дата добавления: 2016-01-18; просмотров: 1482;
