Метод Протодьяконова.
Наиболее распространенная задача технологического эксперимента – найти выход продукта или степень превращения вещества в зависимости от целого ряда факторов. Одновременное воздействие всех факторов при определенном их значении дает некоторый конкретный и практически воспроизводимый результат, поэтому можно говорить о существовании объективной фундаментальной многофакторной зависимости. К сожалению, общий вид такой зависимости неизвестен.
Заведомо известно, что зависимости выхода продукта от вышеназванных факторов нелинейны. Часто эти зависимости экстремальны. Число же факторов, которые необходимо учесть, может доходить до десятка и более. Поэтому более подходящими следует считать методы планирования, в основу которых положена нелинейная множественная корреляция.
Отметим очень важное преимущество формулы М.М. Протодьяконова (старшего) по сравнению с уравнением регрессии, получаемым при обработке данных по методу многофакторного планирования для описания технологических процессов. В уранении Протодьяконова частные зависимости объединяются как произведение, а в уравнении регрессии – как сумма. Следовательно, при нулевом значении любого из факторов в первом случае обобщенная функция обращается в нуль, а во втором сохраняет некоторое значение благодаря ненулевым характеристикам остальных факторов. Последнее - абсурд, поэтому многочленным уравнением регрессии можно пользоваться только в узких пределах.
Матрица – это множество чисел, представленное в виде прямоугольной таблицы с m столбцов и n строк.
Число экспериментов n определяется числом р уровней или значений, задаваемых каждому фактору, по формуле n=р2.
Число факторов не может превышать число уровней более чем на 1, т.е. m ≤ р+1.
Структура матрицы такова, что при проведении всех экспериментов каждый уровень любого фактора встречается один раз с каждым уровнем всех остальных факторов.
Этим обеспечиваетсяусреднение действия любого фактора при выборке результатов эксперимента на любой уровень любого фактора, т.е. обеспечивается тот же самый эффект, какой достигается при бесконечно большом числе экспериментов со случайной вариацией всех факторов. Тем самым открывается возможность для применения законов математической статистики и достигается экономия в числе экспериментов.
Число факторов можно выбирать меньшим, чем имеется в матрице, - от этого структура матрицы не изменится.
Матрица шестифакторного эксперимента на пяти уровнях
(25 опытов).
| № опыта | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Yэ | Yп |
М.М. Протодьяконов предложил для описания статистических многофакторных зависимостей следующую формулу:
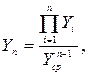
где Yп – обобщенная функция, Yi- частная функция, 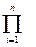 - произведение всех частных функций, Yср- общее среднее всех учитываемых значений обобщенной функции в степени, на единицу меньшей числа частных функций.
- произведение всех частных функций, Yср- общее среднее всех учитываемых значений обобщенной функции в степени, на единицу меньшей числа частных функций.
Обобщенное уравнение – это математическая модель процесса. Обычно обобщенное уравнение используют для оптимихзации процесса.
| <== предыдущая лекция | | | следующая лекция ==> |
| Интегральные микросхемы, их классификация | | | Полупроводниковый диод |
Дата добавления: 2016-01-18; просмотров: 1743;
