Формирование представлений о геометрических фигурах
В соответствии с программой в начальных классах у школьников необходимо сформировать представления о различных геометрических фигурах и их свойствах. Это точка, линии (кривая, прямая, ломаная, отрезок), многоугольники различных видов и их элементы, круг, окружность и др.
В программе четко определены и требования к знаниям и умениям детей о геометрических фигурах. Учитель должен добиться усвоения детьми названий изучаемых геометрических фигур и их свойств, а также сформировать умение выполнять их построение на клетчатой бумаге.
Отмечая особенности изучения геометрических фигур в начальных классах, следует обратить внимание на то обстоятельство, что свойства всех изучаемых фигур выявляются экспериментальным путем в ходе выполнения соответствующих упражнений.
Важную роль при этом играет выбор методов обучения. Значительное место при изучении геометрических фигур и их свойств должны занимать группа практических методов и особенно практические работы.
Систематически должны проводиться такие виды работ, как изготовление геометрических фигур из бумаги, палочек, пластилина, их вырезание, моделирование и др. При этом важно учить детей различать существенные и несущественные признаки фигур. Большое внимание при этом следует уделить использованию приема сопоставления и противопоставления геометрических фигур.
Упражнения, в ходе выполнения которых происходит формирование представлений о геометрических фигурах, предложенные в учебнике, можно охарактеризовать как задания:
- в которых геометрические фигуры используются как объекты для пересчитывания;
- на классификацию фигур;
- на выявление геометрической формы реальных объектов или их частей;
- на построение геометрических фигур;
- на разбиение фигуры на части и составление ее из других фигур;
- на формирование умения читать геометрические чертежи;
- вычислительного характера (сумма длин сторон многоугольника и др.)
Первая встреча детей с геометрическими фигурами происходит еще до школы. У них накапливаются представления о форме, размерах и взаимном расположении различных предметов в окружающем их мире. Эти представления являются необходимой основой для формирования у младших школьников важнейших геометрических представлений, а затем и понятий.
В школе с геометрическими фигурами первоклассники встречаются, начиная с первых уроков, где фигуры выступают в качестве объектов счета. Здесь школьникам целесообразно предлагать упражнения, в ходе выполнения которых они будут называть и пересчитывать демонстрируемые учителем фигуры, находить их у себя в наборах и выкладывать перед собой заданное их количество.
Например, учитель выставляет на наборное полотно 5 треугольников и ведет с детьми разговор в таком плане:
- Какие фигуры я выставила?
- Сколько треугольников?
- Найдите у себя в наборе столько же треугольников и положите их перед собой на столе.
В результате такой работы дети учатся узнавать фигуры по форме, выделять ту или иную из числа других и давать им название.
В это же время происходит знакомство детей с тетрадью, страницы которой покрыты различными линиями (прямыми горизонтальными, вертикальными и наклонными, пересекающимися и непересекающимися). Эта своеобразная геометрия листа дает хороший материал для формирования геометрических представлений детей, и его необходимо использовать.
Этот период, формально не связанный с изучением геометрических фигур, фактически занимает важное место в этом процессе, так как в ходе такой работы у детей формируются определенные представления о геометрических фигурах, но происходит это в основном на интуитивном уровне (без выделения существенных признаков объекта).
Дальнейшая работа по изучению геометрических фигур проводится уже в соответствии с программой и учебником. При этом, выполняя соответствующие упражнения и организуя деятельность детей, следует обратить самое серьезное внимание на выделение существенных признаков каждой изучаемой фигуры.
С точкой учащиеся знакомятся с первых шагов обучения. Это основное, неопределяемое понятие. Готовясь к письму цифр, они выполняют задания: поставьте точку в середине клетки; соедините поставленные точки отрезками. Точками являются концы отрезков, вершины многоугольников.
Позже учащиеся знакомятся с обозначением точек заглавными латинскими буквами: А, B, C, D, K, M, N, O, Q, E и др. , которые пишутся около точки.
Упражнения: 1) Поставить точки и обозначить их буквами. 2) Выписать точки, которые лежат внутри круга, вне круга, на окружности.
Представление о прямой, кривой линиях происходит в процессе выполнения практических упражнений. Это основные, неопределяемые понятия. При этом прямую линию сопоставляют с кривой. Представление о прямой линии дает туго натянутая линия, линия горизонта в степной местности. Необходимо научиться узнавать прямую линию, изображенную в любом положении на плоскости. С целью выработки практических умений дается задание – начертить прямые и кривые линии, найти и показать их в окружающих предметах, на чертежах.
С отрезком учащиеся знакомятся также практически: учитель предлагает на прямой отметить две точки и поясняет, что часть прямой от одной точки до другого называют отрезком прямой, или кратко – отрезком, а точки – концами отрезка. Выполняются упражнения: показать отрезок на чертеже, показать концы отрезка; построить отрезок, построить отрезок данной длины; построить отрезок через три точки, лежащие на одной прямой показать все получившиеся при этом отрезки.
Опираясь на понятие отрезка, учащиеся знакомятся с ломаной линией. Для этого учитель предлагает построить по образцу линию из палочек. Дается название новой линии. Учащиеся строят ломаные линии на доске и в тетрадях: ставят несколько точек, не лежащих на одной прямой, и соединяют их отрезками. Учащиеся подсчитывают, сколько отрезков (звеньев) содержит ломаная линия. Так же с помощью наглядного пособия вводятся понятия незамкнутой и замкнутой ломаной линии. Учитель предлагает показать начало (начало первого отрезка) и конец (конец последнего отрезка) и дает название такой ломаной - незамкнутая ломаная линия. Затем предлагает соединить начало и конец ломаной линии и дает название ломаной – замкнутая ломаная линия. При этом звенья соединяют так, чтобы они, кроме вершин, не имели общих точек.
В процессе упражнений устанавливают связь между замкнутой ломаной линией и многоугольником, для которого ломаная линия является границей. Замкнутая ломаная линия их трех звеньев ограничивает треугольник, из четырех звеньев – четырехугольник.
Затем учащихся знакомят с измерением ломаных линий. Для этого необходимо измерить звенья ломаной и сложить полученные длины.
Понятие о периметре многоугольника дается в процессе решения конкретной задачи на нахождение суммы длин сторон треугольника (четырехугольника). Выполняются упражнения:: найти сумму длин сторон треугольника (разностороннего, равностороннего), четырехугольника (прямоугольника).
Понятия многоугольника, круга, угла формируются в течение первого года обучения и в последующих классах.
При изучении чисел первого десятка геометрические фигуры используются как дидактический материал. Опираясь на него, учащиеся считают предметы, решают задачи, вычисляют, составляют орнаменты, сравнивают, классифицируют. Попутно уточняются представления об отдельных фигурах, запоминаются их названия: круг, треугольник, четырехугольник, квадрат, овал.
Далее приступают к изучению отдельных видов многоугольников. На этом этапе вычленяют элементы многоугольников: стороны, углы, вершины. Так, при изучении числа 3 рассматривают понятие треугольника, а числа 4 – четырехугольника. С помощью моделей выделяют элементы треугольника: три стороны (отрезка), три вершины (точки), три угла. Выполняются упражнения: сложить треугольник; найти и раскрасить треугольники; указать предметы, имеющие форму треугольника; выделить на чертеже и показать треугольники. При этом рассматриваются треугольники разных видов (равносторонние и разносторонние, прямоугольные, тупоугольные и остроугольные). Это способствует формированию правильного представления о треугольнике.
Таким же образом рассматривают четырехугольники. Подмечается связь между числом элементов и названием фигуры (три угла – треугольник, четыре угла – четырехугольник, пять углов – пятиугольник). Понятие многоугольника можно ввести как обобщение рассмотренных видов многоугольников, а также как замкнутую ломаную линию.
В процессе работы над многоугольниками учащиеся получают первые сведения об углах. Угол образуют две стороны многоугольника, выходящие из одной из вершин.
Далее учащиеся знакомятся с прямым углом. Для этого лист бумаги дважды перегибают пополам и устанавливают, что получившиеся при этом две пересекающиеся прямые линии образуют четыре одинаковых угла. Учитель сообщает, что такие углы называют прямыми. Наложением устанавливают, что все получившиеся прямые углы равны. Пользуясь моделью прямого угла, учащиеся находят прямые и непрямые углы на окружающих предметах, на чертеже. Учащиеся знакомятся с чертежным треугольником. Выполняются упражнения: найти прямые углы на чертеже; найти прямые углы в данных многоугольниках; начертить прямой угол в тетради, используя ее разлиновку; начертить треугольник (четырехугольник), имеющий прямой угол, и др.
Для правильного представления об углах используют модель «раздвижного угла» (малку). Учащиеся убеждаются, что величина угла зависит не от длины его сторон, а от взаимного положения сторон относительно друг друга.
Понятие угла закрепляется в дальнейшем в процессе изучения многоугольников, например, при рассмотрении прямоугольника. Среди нескольких четырехугольников учащиеся находят четырехугольники с одним, двумя прямыми углами, а также четырехугольники, у которых все углы прямые. Дается определение прямоугольника. Выполняются упражнения: найти прямоугольники в окружающей обстановке, найти прямоугольники среди других четырехугольников, среди многоугольников; найти прямоугольники на чертеже; вырезать их из бумаги в клетку; построить в тетради.
На следующем этапе учащиеся знакомятся с одним из свойств прямоугольника: противоположные стороны прямоугольника равны между собой.
Далее рассматривается нахождение периметра многоугольников: треугольника, четырехугольника, в частности, прямоугольника. Рассматривают все способы нахождения периметра: 1) измеряют каждую сторону и складывают полученные числа; 2) измерить длину и ширину, затем умножить каждое из этих чисел на 2 и полученные произведения сложить.
Из множества прямоугольников вычленяют квадраты – прямоугольники с равными сторонами. Квадрат – это частный случай прямоугольника. Выполняются упражнения: найдите среди прямоугольников квадраты; покажите прямоугольники, которые нельзя назвать квадратами; найдите среди четырехугольников квадраты. Периметр квадрата находят, умножая длину стороны на 4.
Знакомство с окружностью происходит практически: учащиеся учатся строить окружности с помощью циркуля. Рассматриваются элементы окружности и круга – центр и радиус.
Сопоставив круг с многоугольником, учащиеся устанавливают, что границей многоугольника является замкнутая ломаная линия, а границей круга – замкнутая кривая линия – окружность. Чтобы учащиеся не смешивали круг и окружность, выполняются упражнения: проведите окружность и раскрасьте круг, отметьте центр круга или окружности, отметьте точки, лежащие внутри круга, вне круга, на окружности.
Знакомству с геометрическими фигурами и их свойствами способствуют и простейшие задачи на построение. В ходе их выполнения дети учатся пользоваться чертежными инструментами, у них формируются чертежные навыки.
Первые построения выполняются по образцу. Научив детей выделять данную фигуру (отрезок, прямоугольник и др.) из множества других фигур, мы даем им задание начертить такую же, как в книге, как на доске и т.д.
Большая часть задач на построение - это в основном метрические задачи на построение, в которых обращается внимание только на размеры и форму искомой фигуры. Например, построить прямоугольник, периметр которого 12 см.
Процесс решения задачи на построение разбивается обычно на 4 этапа: анализ, построение, доказательство и исследование.
В начальных классах эти этапы явно не присутствуют, но учитель должен начинать неявное включение учащихся в выполнение этой работы. В зависимости от содержания решаемых задач и целей их решения можно варьировать число этих этапов.
Пример.
1) Построение и исследование.
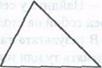
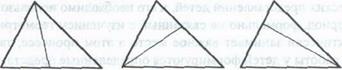
Задача. Начерти такой треугольник. Проведи один отрезок так, чтобы получилось еще два треугольника.
После выяснения, как расположен треугольник (по числу клеточек), приступаем к исследованию (Сколько отрезков надо провести? Сколько можно провести разных отрезков?).
2) Построение и доказательство.
Задача. Начерти прямой угол. (После построения с помощью модели прямого угла доказываем, что построение выполнено верно).
3) Анализ и построение.
Задача. Начерти четырехугольник, у которого два угла прямые, а два других – непрямые.
(Следует использовать таблицу с четырехугольником, по которой ведется анализ).
При выполнении построений необходимо учить детей правильно пользоваться линейкой, карандашом и т.д. Здесь надо предъявлять к учащимся требования не меньше, чем при формировании навыков письма и счета.
Дата добавления: 2016-01-18; просмотров: 4454;
