Монолитные ребристые перекрытия с плитами, опертыми по контуру

Существует два вида таких перекрытий. В перекрытиях первого вида балки располагаются по осям колонн, шаг которых 4...6 м (рис. 9.8, а). Балки имеют одинаковую высоту поперечных сечений. Соотношение сторон плит 1...1.5. Перекрытия второго вида, называемые кес­сонными, отличаются более частым расположением балок, отсутствием промежуточных колонн и малыми размерами плит, не превышающими 2 м (рис. 9,8, б). Перекрытия с плитами, опертыми по контуру, менее экономичны, чем с балочными плитами, при той же сетке колонн, но эстетически они выглядят лучше и применяются для перекрытия зданий общественного назначения: вестибюлей, залов и т. п.

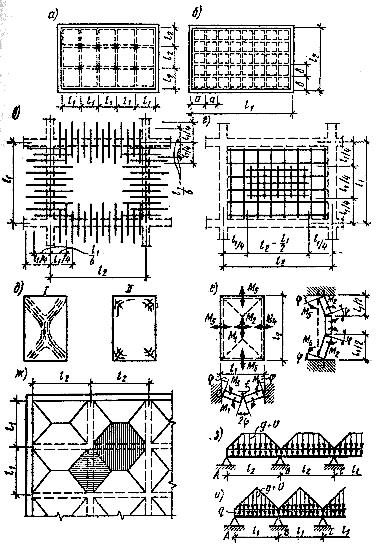
Рис. 9.8. Ребристые монолитные перекрытия с плитами,

опертыми по контуру

Плита, опертая по контуру, работает в двух направлениях и армируется сварными сетками, укладываемыми в пролете понизу, а у опор (над балками) — поверху. При пролетах плиты более 2,5 м применяют раздельное армирование. Нижнюю арматуру выполняют из двух сеток с одинаковой площадью сечения рабочей арматуры в каждом направлении. В целях экономии одна сетка доводится до опор, а другая размещается в средней части и не доводится до опор на расстояние ¹/₄l₁, если плита примыкает к балке (рис. 9.8, г), или на ¹/₈l₁ при свободном опирании плиты. Верхняя арматура плиты (над балками) выполняется в виде сеток, у которых рабочие стержни располагаются в направлении, перпендикулярном балке, и заходят в пролеты через один на расстояния ¹/₄l₁ и ¹/₆l₁ (рис. 9.8, в).

Для расчета плит, опертых по контуру существуют два практических метода: по упругой стадии и по предельному равновесию. Расчет по упругой стадии применяют для плит, в которых трещины не допускаются. Точный расчет плит, опертых по контуру, представляет достаточно сложную задачу теории упругости. Он сводится к интегрированию дифференциальных уравнений упругой пластинки. Для плит из однородного материала эта теория разработана достаточно подробно. Для практических расчетов плит в упругой стадии существуют приближенные методы и составлены вспомогательные таблицы, позволяющие определить усилия в плитах при разных граничных условиях и нагрузках [24].

Расчет плит, в которых по условиям эксплуатации допускаются трещины, производят методом предельного равновесия. При его использовании должна быть известна схема разрушения конструкции. Опытами установлено, что в предельном состоянии по прочности в плите образуется ряд линейных пластических шарниров: на опорах – сверху вдоль балок, в пролетах – снизу по биссектрисам углов плиты и в середине пролета – вдоль длинной стороны плиты (рис. 9.8. д). Исходя из этого, плиту рассматривают как систему жестких дисков, соединенных между собой пластическими шарнирами по линиям излома. Значение момента в пластическом шарнире на единицу его длины зависит от площади сечения рабочей арматуры A_s и определяется по формуле

В общем случае каждая панель плиты перекрытия испытывает действие шести изгибающих моментов: двух пролетных M₁ и M₂ и четырех опорных M₃, M₄, M₅, M₆ (рис. 9.8, е).

Для обеспечения равновесия плиты необходимо и достаточно, чтобы имело место равенство работ внешних W_q и внутренних W_M усилий на возможных перемещениях. При равномерно распределенной нагрузке q это условие имеет вид

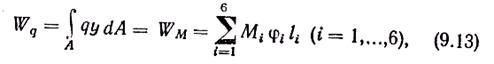
где у — перемещения плиты в рассматриваемой точке; M_i — момент в i-м шарнире пластичности, приходящийся на единицу его длины; φ_i — угол поворота дисков в i-м шарнире пластичности; l_i — длина i-го пластического шарнира.

Нетрудно видеть, что ∫ qydA представляет собой объем фигуры перемещений плиты

где f — прогиб середины плиты.

Тогда работа внешней нагрузки

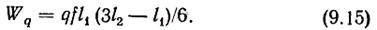
Работа внутренних усилий — изгибающих моментов на соответствующих углах поворота φ (рис. 9.8, е)

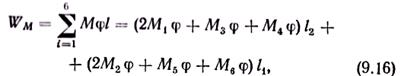
Учитывая небольшую величину φ, принимают

Из условия равенства работ (9.13) с учетом (9.15) и (9.16) получают

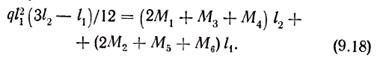
В том случае, когда в приопорных полосах шириной l₁/4 арматура поставлена в половинном количестве (рис. 9.8, г), пролетные моменты в этих полосах будут М₁/2 М₂/2.

Приведенные формулы содержат шесть неизвестных моментов. Задавшись их соотношениями, получим только одно неизвестное М, определив которое, по принятым соотношениям находят и остальные моменты [12].

В практических расчетах определение моментов упрощается. Так, для средней панели квадратной плиты (l₁ = 1₂ = 1), окаймленной по периметру балками, задавшись М₁=М₂=М₃=М₄=М₅=М₆ и приняв обрыв одной из нижних сеток на расстояние ¹/₄l от балок, получают для опорных и пролетных моментов

Для свободно опертой квадратной плиты все опорные моменты равны нулю, а пролетные — М₁=M₂=M, тогда при обрыве одной нижней сетки на ¹/₈l от опоры

После вычисления моментов подбирают арматуру в пролетах и на опорах как для элементов прямоугольного сечения с одиночной арматурой.

В плитах, окаймленных по всему контуру монолитно связанными с ними балками, возникает распор, повышающий их несущую способность. Поэтому при подборе арматуры значения моментов, определенные расчетом, следует уменьшать до 20% [12].

Плиты, опертые по контуру, передают нагрузку на балки в соответствии с грузовыми площадями (рис. 9.8, ж). Балки рассчитывают как обычные неразрезные с учетом перераспределения усилий. При этом расчетные пролеты принимают равными расстоянию между гранями колонн, а для крайних пролетов — между гранью колонны и осью опоры на стене.

Моменты в первом пролете и на первой промежуточной опоре

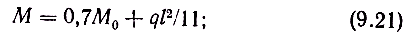
в средних пролетах и на средних опорах

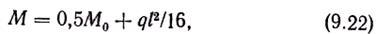
где М₀ — момент в свободно опертой балке;

при треугольной нагрузке (рис. 9.8, и)

при трапецеидальной нагрузке (рис. 9.8, з)

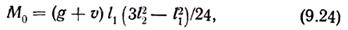
где (g+v) — расчетная нагрузка на 1 м² плиты; q — нагрузка от массы балки и части перекрытия с временной нагрузкой на ней.

Поперечные силы в таких балках определяют по выражениям

где Q₀ — балочная поперечная сила.

Площадь сечения продольной рабочей арматуры в пролетах определяют как для тавровых сечений, а на опорах — как для прямоугольных. И в пролетах и на опорах балки армируют сварными каркасами.