Метод Квайна −Мак-Класки
Этот метод ориентирован на числовое задание ФАЛ в виде кубического комплекса, состоящего из 0-кубов. Метод представляет собой формализованный на этапе нахождения простых импликант метод Квайна. Основной недостаток метода Квайна – необходимость выполнения полного сравнения (склеивания) всех первичных импликант. В случае большого их количества сложность этого сравнения существенно возрастает. В рассматриваемом методе все исходные n-кубы разбиваются на непересекающиеся подгруппы по количеству единиц в кубе. Пусть, например, задана функция
f СДНФ(x1x2x3x4) = V (2, 3, 4, 6, 9, 10, 11, 12).
Сформируем кубический комплекс K, состоящий из 0-кубов:
K=(0010, 0011, 0100, 0110, 1001, 1010, 1011, 1100).
Выполнив разбиение комплекса K на группы, получим:
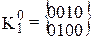 ,
,  ,
, 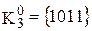 .
.
Попарное сравнение можно проводить только между соседними по номеру группами кубов, так как кубы, порождающие новые кубы, должны иметь кодовое расстояние, равное 1. В результате сравнения кубов получим:
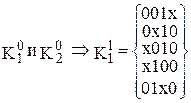 ,
, 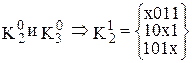 .
.
После выполнения первого шага алгоритма простых импликант не выявлено. Полученные 1-кубы разобьем на n групп кубов в зависимости от местоположения свободной координаты в кубе.
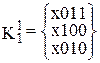 ,
, 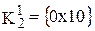 ,
, 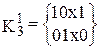 ,
, 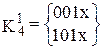 .
.
Далее выполняется сравнение кубов внутри каждой из групп. В результате могут быть получены 2-кубы, которые, в свою очередь, аналогично 1-кубам будут объединены в группы по совпадению свободных координат и вновь будет выполнено сравнение. На каждом шаге сравнения выявляются кубы, не участвовавшие в образовании новых кубов, и исключаются из дальнейшего упрощения. Для рассматриваемого примера сравнение в группах 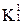 …
… 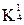 привело к образованию двух новых кубов х01х и х01х и кубов, не образовавших новых {х100, 0х10, 10х1, 01х0}.
привело к образованию двух новых кубов х01х и х01х и кубов, не образовавших новых {х100, 0х10, 10х1, 01х0}.
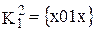 ,
, 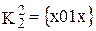 .
.
Дальнейшее сравнение не приводит к формированию новых кубов 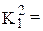
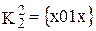 . Таким образом, получено множество простых импликант:
. Таким образом, получено множество простых импликант:
fсокр.ДНФ={х100, 0х10, 10х1, 01х0, х01х} .
Далее аналогично методу Квайна строится импликантная таблица (табл.15). Формирование минимального покрытия сводится к выявлению обязательных простых импликант и построению на их основе тупиковых форм.
Таблица 15
| Простые импликанты | Конституенты единицы | |||||||||
| Х100 | * | * | ||||||||
| 0х10 | * | * | ||||||||
| 10х1 | * | * | ||||||||
| 01х0 | * | * | ||||||||
| Х01х | * | * | * | * |
Из таблицы следует, что простые импликанты x100, 10x1, x01x являются обязательными. Оставшиеся две простые импликанты не являются обязательными и образуют следующие две тупиковые формы.
f МДНФ = {х100, 10х1, х01х, 0х10} – 1-я тупиковая форма;
f МДНФ = {х100, 10х1, х01х, 01x0} – 2-я тупиковая форма.
Алгоритм извлечения (Рота)
Метод Рота ориентируется на задание логической функции в форме произвольного кубического покрытия, что позволяет упростить процесс подготовки выражения для минимизации. Достоинство алгоритма Рота – полная формализация действий на всех этапах минимизации функции.
Специальные логические операции алгоритма Рота: *, ∩ , #
Реализация алгоритма извлечения осуществляется на основе специальных логических операций, которые позволяют полностью формализовать процесс получения минимальной формы.
Операция умножения кубов (*).Операцияумножения кубов а=а1а2...аn и b=b1b2...bn обозначается как с=а*b и служит для образования r-куба, противоположные (r-1) грани которого содержатся в кубах а и b. Предварительные координаты куба c определяются в соответствии с таблицей, приведенной ниже.
 * *
| х | ||||
| Y | |||||
| у | ||||
| x | х |
î ______________Ú_________________þ
bi
Окончательно координаты куба формируются:
 m(a1*b1)m(a2*b2) ... m(an*bn), если ai*bi=y только для одного i,
m(a1*b1)m(a2*b2) ... m(an*bn), если ai*bi=y только для одного i,
a*b=
Æ, если ai*bi=y для i ³ 2,
где m(ai*bi) – окончательная i-я координата куба с; m(0)=0; m(1)=1; m(x)=x;
y – условное обозначение того, что координаты ai и bi противоположны.
Эта операция соответствует операции склеивания: образуется новый r-куб, если кодовое расстояние двух исходных кубов равно 1.
Рассмотрим некоторые примеры, графическая интерпретация которых приведена на рис. 26.
1) 011 2) 11х
*001*01х
0y1 Þ 0x1– ребро покрывает две вершины у1х Þ х1х – грань
3) 0х1 4) х1х
*1х0 *011
уху Þ Æ – две координаты имеют значение у. 011
 Операция пересечения кубов (∩).Операция пересечения кубов а=а1а2...аn и b=b1b2...bn обозначается как с=а∩b и служит для выделения куба с=с1с2...сn , являющегося общей частью кубов а и b. Координаты с1с2...сn определяются согласно следующей таблице.
Операция пересечения кубов (∩).Операция пересечения кубов а=а1а2...аn и b=b1b2...bn обозначается как с=а∩b и служит для выделения куба с=с1с2...сn , являющегося общей частью кубов а и b. Координаты с1с2...сn определяются согласно следующей таблице.
∩ 
| x | ||||
| Æ | |||||
| Æ | ||||
| x | x |
î______________Ú_________________þ
bi
 m(a1∩b1)m(a2∩b2) ... m(an∩bn,),
m(a1∩b1)m(a2∩b2) ... m(an∩bn,),
a∩b=
Æ, если существует такое i, для которого ai ∩ bi =Æ,
где m(ai*bi) – окончательная i-я координата куба с; m(0)=0; m(1)=1; m(x)=x.
Рассмотрим примеры и их графическую интерпретацию (рис. 27).
1) Ç100 2) Ç1х0
00110х
Æ0Æ Þ Æ общей части у 100 Þ 100 общая часть
кубов нет кубов (рёбер) - вершина
3) Çх1х 4) Ç0хх
0хх 0х0
01х Þ 01х общая часть – ребро 0х0 ( совпадает с
операцией *)
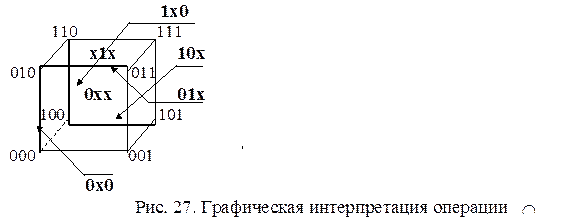
Операция вычитания кубов (#).Операция вычитания из куба а=а1а2...аn куба b=b1b2...bn обозначается как с=а#b и служит для удаления из куба а общей части кубов а и b.
Координаты куба с формируются согласно следующей таблице.
# 
| x | ||||
| z | y | z | |||
| y | z | z | ||
| x | z |
î ______________Ú_________________þ
bi
 Æ, если для любого i аi#bi=z,
Æ, если для любого i аi#bi=z,
c=а#b= a, если существует такое i, что аi#bi=y,
U а1а2...аi-1 ai аi+1 ... аn, если ai равно 0 или 1 для одного или
i=1 нескольких i,
где z означает, что координаты совпадают, а y, как для операции *, означает, что координаты ai и bi противоположны.
По этим ai-координатам производится объединение (U) кубов, получаемых в результате замены в кубе а символа х на соответствующее значение (0,1) координаты ai. Рассмотрим примеры выполнения операции # и их графическую интерпретацию (рис. 28).
1) #х1х 2) # х1x
x11110
 zz0 Þ x10 0z1 Þ 01x
zz0 Þ x10 0z1 Þ 01x
3) #хx1 4) #х11 x11
x10 xx1
 z0y Þ xx1 zzz Þ Æ
z0y Þ xx1 zzz Þ Æ

5) # 0ххx
хх01
 zz10 Þ 0x1x
zz10 Þ 0x1x
0xx0
Далее рассмотрим алгоритм извлечения (Рота) на примере минимизации булевой функции, заданной покрытием С0 (рис.29).
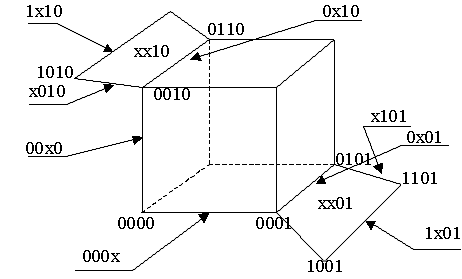
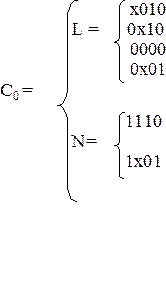
Рис. 29. Геометрическое задание исходного покрытия
Исходное покрытие С0 задано объединением множеств кубов L и N. Кубы комплекса N − это наборы, на которых функция не определена и которые включаются в покрытие ради возможного дополнительного упрощения комплекса L в процессе минимизации. Минимальное покрытие комплексов L и N, С min называется К-покрытием L.
Общий алгоритм построения минимального К-покрытия называется алгоритмом извлечения и состоит в следующем:
▪ нахождении множества Z простых импликант комплекса К;
▪ выделении L-экстремалей на множестве Z;
▪ применении алгоритма ветвления при отсутствии L-экстремалей;
▪ нахождении абсолютно минимального покрытия из некоторого множества избыточных покрытий.
Дата добавления: 2016-01-09; просмотров: 1652;
