Критерии выбора системы счисления

Сформулируем требования, которым должна удовлетворять система счисления для ЭВМ.

1. Простота технической реализации. Для хранения чисел в той или иной системе счисления используются n-позиционные запоминающие элементы. Элемент будет тем проще, чем меньше состояний требуется для запоминания цифры числа, то есть чем меньше основание системы счисления. Двухпозиционными элементами, имеющими два состояния, являются, например:

§ электромеханическое реле (контакты замкнуты – 1, разомкнуты – 0);

§ конденсатор (заряжен – 1, разряжен – 0);

§ полупроводниковый элемент (если открыт, то хранит 0, иначе − 1) и

др.

Трехпозиционные элементы более редки. Например, конденсатор для запоминания цифр 0 – разряжен, 1– заряжен в одном направлении, 2 – в другом. Таким образом, реализация n-позиционных элементов более сложна, чем двухпозиционных.

2. Наибольшая помехоустойчивость кодирования цифр. Положим, что при технической реализации любой системы счисления диапазон изменения электрического значения наибольшего и наименьшего числа одинаков. Очевидно преимущество систем с меньшим основанием, так как представление соседних цифр в этих системах отличается друг от друга больше, чем для систем с большим основанием.

Очевидно, что при наложении помехи на основной сигнал, соответствующий некоторой цифре, наиболее вероятна ошибка в устройствах, для которых используется система счисления с наибольшим основанием (рис.1). Следовательно, при увеличении основания помеха может привести к искажению числа.

3. Минимум оборудования. Пусть r - количество цифр в числе, n - количество разрядов в каждом числе, тогда D = r∙n - количество цифроразрядов на одно число. Надо найти такую систему счисления, которая имеет минимальное количество цифроразрядов при заданном количестве чисел N:

N= ,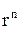

n= ,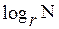

D= = .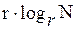

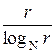Будем считать, что основание системы счисления может принимать любые значения, а не только целочисленные, изменяясь непрерывно, а не дискретно. Соответственно количество цифроразрядов может быть также величиной непрерывной, связанной с основанием системы счисления логарифмической зависимостью:

D(r)= .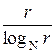

Это позволит свести задачу нахождения D(b)_min к исследованию функции на экстремум:

,

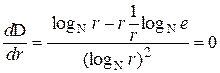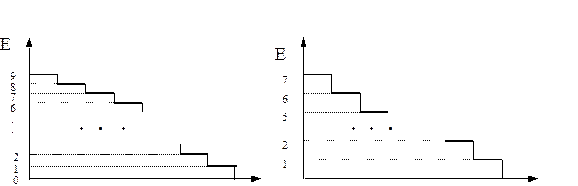
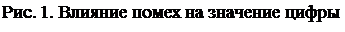следовательно, r_опт=e @2,718. Так как основание системы счисления должно быть целым числом, то основанием, наиболее близким к e, является основание r = 3. Но для реализации этого нужен элемент с тремя стабильными состояниями.

Выясним, насколько каждое из целочисленных оснований r_i уступает r_опт. Для этого оценим каждое основание r_i исходя из выражения

D _{i (отн)}= ,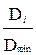

где D_min= r_опт log _{r опт}N=e ∙ ln N.

Следовательно, получим:

D(r)= .

Выполнив расчеты для некоторых оснований, получим следующие результаты:

4. Простота арифметических действий. Чем меньше цифр в системе счисления, тем проще арифметические действия над ними. Таблицы для выполнения четырех арифметических операций будут усложняться с увеличением основания системы счисления. Это можно принять за косвенное доказательство выдвинутого положения.

5. Наибольшее быстродействие. Как будет показано далее, операции вычитания, умножения и деления могут быть выполнены посредством операции алгебраического сложения. Алгебраическое сложение чисел часто сводится к их арифметическому сложению. Таким образом, взяв его за базовое, вычислим соотношение времени, необходимого на сложение:

T_сл = n t_пер = t_пер log_bN.

Для упрощения оценки перейдем от абсолютной оценки к относительной:

δ = ,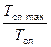

T_{сл max} = T_{сл (2)} = t_пер log₂N,

δ = ,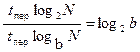

r_i 2 3 4 5 . . .

δ 1,00 1,58 2,00 2,32 . . .

6. Простота аппарата для выполнения анализа и синтеза цифровых устройств. Математическим аппаратом, позволяющим относительно просто и экономно строить цифровые схемы, является алгебра логики. Наибольшее распространение и законченность вследствие своей простоты получила двузначная логика.

7.Удобство работы с ЭВМ. Наиболее удобной системой счисления для работы человека является десятичная система счисления. Но внутри ЭВМ для выполнения арифметических операций числа из десятичной системы счисления требуется переводить во внутреннюю систему счисления.

Для системы счисления с основанием, большим 10, появляются новые цифры. Таким образом, система счисления должна иметь минимальное число цифр, так как в этом случае можно пользоваться младшими цифрами десятичной системы счисления.

8.Возможность представления любого числа в рассматриваемом диапазоне величин.

9.Единственность представления числа.