Рассчитать Моду по данным таблицы.
По максимальной частоте найдем соответствующую группу и варианту:
fmax=8
М0=4+1(8-5)/((8-5)+(8-4)=4,4
Мода=4 разряд. Наиболее часто встречающийся разряд рабочих 4.
Рассчитать Медиану по данным таблицы.
Определяем медиану, для этого найдем медианный интервал по накопленной частоте. Нужная накопленная частота определяется путем суммирования частот f до тех пор, пока очередная накопленная частота впервые не превысит половину совокупности n+1/2 или n/2 .
Для четного ряда 20/2= 10→S= 14 → Ме =4 разряд.
Половина всех рабочих имеет тарифный разряд меньше 4, другая половина больше 4.
Свойства средней арифметической.
1. Средняя арифметическая из постоянных чисел равна этому постоянному числу.
Пусть х = a, тогда
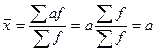 .
.
2. Если веса всех вариантов пропорционально изменить, т.е. увеличить или уменьшить в одно и то же число раз, то средняя арифметическая нового ряда от этого не изменится. Пусть f уменьшим в к раз. Тогда.
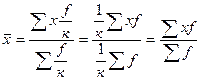
3. Если все варианты уменьшить или увеличить на какое-либо число, то средняя арифметическая нового ряда уменьшится или увеличится на столько же.
Уменьшим все варианты х на 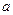 , т.е.
, т.е. 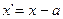 , тогда
, тогда
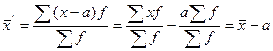 .
.
Среднюю арифметическую первоначального ряда можно получить, прибавляя к средней арифметической нового ряда, ранее вычтенное из вариантов число a, т.е.
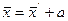 .
.
4. Если все варианты уменьшить в к раз, то средняя арифметическая нового ряда уменьшится в к раз.
Пусть 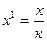 , тогда .
, тогда .
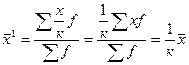
Среднюю арифметическую первоначального ряда можно получить, увеличив среднюю арифметическую нового ряда в 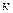 раз:
раз:
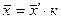 ,
,
5. Сумма положительных и отрицательных отклонений отдельных вариантов от средней, умноженных на веса, равна нулю.
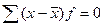 .
.
Дата добавления: 2016-01-09; просмотров: 1040;
