Энергия систем заряженных тел. Энергия электростатического
Поля
Электростатические силы взаимодействия консервативны и значит, система зарядов обладает потенциальной энергией, рассмотрим точечные заряды Q1 и Q2, находящиеся на расстоянии "r" друг от друга. Согласно (2.7) и (2.8) каждый из них в поле другого обладает энергией  ,
, 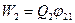 , где
, где 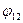 и
и 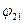 - соответственно потенциалы, создаваемые зарядом Q2 в точке нахождения заряда Q1, и зарядом Q1 в точке нахождения Q2. Используя (2.8), имеем
- соответственно потенциалы, создаваемые зарядом Q2 в точке нахождения заряда Q1, и зарядом Q1 в точке нахождения Q2. Используя (2.8), имеем 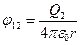 ;
; 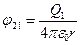 и следовательно
и следовательно
W1 = W2 = W и 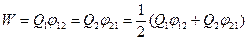 .
.
Добавляя к системе из двух зарядов последовательно заряды Q3, Q4, … Qn, можно убедиться что энергия системы неподвижных точечных зарядов равна
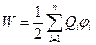 , (3.24)
, (3.24)
где 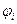 - потенциал поля, создаваемого в точке нахождения заряда Q1, всеми зарядами кроме самого заряда Q1.
- потенциал поля, создаваемого в точке нахождения заряда Q1, всеми зарядами кроме самого заряда Q1.
Рассмотрим теперь уединенный проводник, заряд, емкость и потенциал которого равны соответственно Q,, C и 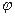 . Увеличим заряд проводника на dQ. Для этого согласно (2.10) и (3.24) надо затратить работу
. Увеличим заряд проводника на dQ. Для этого согласно (2.10) и (3.24) надо затратить работу 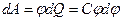 , а что бы зарядить тело от нулевого потенциала до
, а что бы зарядить тело от нулевого потенциала до 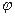 необходима работа
необходима работа
 . (3.25)
. (3.25)
Энергия заряженного уединенного проводника равна работе затраченной для его зарядки
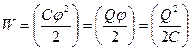 . (3.26)
. (3.26)
Как и всякий заряженный проводник, заряженный конденсатор обладает энергией, которая согласно (3.26) равна
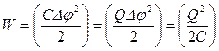 . (3.27)
. (3.27)
Синхронно с процессом зарядки конденсатора между его обкладками возникает электростатическое поле. Поэтому энергия заряженного конденсатора (3.27) - это и есть энергия электростатического поля возникшего между его обкладками.
Однако логичней выражать энергию электростатического поля через характеристики самого поля. Используя выражения: 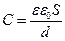 и
и 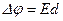 , получим из (3.26)
, получим из (3.26)
 , (3.28)
, (3.28)
где V = (Sd) - объем конденсатора.
Энергию поля так же характеризуют величиной, называемой объемная плотность энергии поля (энергией единицы объема с размерностью 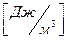 ):
):
 . (3.29)
. (3.29)
Эти выражения справедливы только для изотропных диэлектриков, для которых 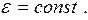
Дата добавления: 2016-01-09; просмотров: 1009;
