Система управления стиральных автоматических машин Fuzzy Logic

В последнее десятилетие в области автоматического управления различными техническими устройствами и, в частности, в изделиях бытовой техники и техники сферы сервиса получили развитие системы, основанные на так называемой «Нечеткой логике» (Fuzzy Logic). Впервые термин Fuzzy Logic был введен американским профессором азербайджанского происхождения Лотфи Заде в 1965 г. в работе "Нечеткие множества", опубликованной в журнале «Информатика и управление». Основанием для создания новой теории послужил спор профессора со своим другом о том, чья из жен привлекательнее. К единому мнению они, естественно, так и не пришли. Это вынудило Заде сформировать концепцию, которая выражает нечеткие понятия типа "привлекательность" в числовой форме. Областью внедрения алгоритмов нечеткой логики являются всевозможные экспертные системы, в том числе: нелинейный контроль за производственными процессами; самообучающиеся системы, исследование рисковых и критических ситуаций; распознавание образов и др. В отличие от традиционной математики, требующей на каждом шаге моделирования точных и однозначных формулировок закономерностей, нечеткая логика предлагает иной уровень - подход, при котором постулируется лишь минимальный набор закономерностей. Нечеткие числа, получаемые в результате "не вполне точных измерений", во многом аналогичны распределениям теории вероятностей. В пределе, при возрастании точности, нечеткая логика приходит к стандартной, Булевой. По сравнению с вероятностным методом, нечеткий метод позволяет резко сократить объем производимых вычислений, что, в свою очередь, приводит к увеличению быстродействия нечетких систем.

Базовые понятия нечеткой логики

Прогноз погоды обычно выглядит так: завтра температура воздуха +5°С, возможен дождь. В этом случае даже профессиональные синоптики не могут точно сказать, будет дождь или нет. Это и есть проявление нечеткой логики: погода завтра может быть в данном случае как просто пасмурной, так и дождливой: события здесь предсказываются с некоторой долей уверенности (рангом). Рассмотрим теперь другой пример, связанный с возрастом человека (рис. 6.15). До 16 лет нельзя однозначно утверждать, что человек молодой (например, 15-летние относятся к категории "молодой" с рангом около 0,9). Зато диапазону от 16 до 30 лет можно присвоить ранг 1, т.е. человек в этом возрасте действительно молодой. После 30 лет человек считается уже не молодым, но еще и не старым, здесь принадлежность (ранг) термина "молодой" возрасту будет принимать значения в интервале от 0 до 1. И чем больше возраст человека, тем меньше становится его принадлежность к соответствующему терму (см. ниже), т.е. ранг будет стремиться к 0.

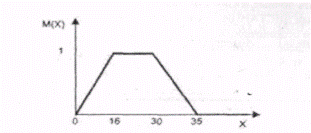
Рис. 6.15. Нечеткое множество для термина "молодой".

Таким образом, было получено нечеткое множество, описывающее понятие молодости для всего диапазона возрастов человека. Если ввести остальные термины (например, "очень молодой", "старый" и т.д.), то можно охарактеризовать такую переменную, как возраст, состоящую из нескольких нечетких множеств и полностью перекрывающую весь жизненный период человека. Ключевыми понятиями нечеткой логики являются:

— фаззификация — сопоставление множеству значений аргумента (х) некоторой функции принадлежности М(х), т.е. перевод значений (х) в нечеткий формат (см. пример с термином "молодой);

— дефаззификация — процесс, обратный фаззификации.

Все системы с нечеткой логикой функционируют по одному принципу: показания измерительных приборов фаззифицируются (переводятся в нечеткий формат), обрабатываются, дефаззифицируются и в виде привычных сигналов подаются на исполнительные устройства. Функция принадлежности — это не вероятность, т.к. нам неизвестно статистическое распределения, нет повторяемости экспериментов. Так, если взять из рассмотренного выше примера прогноза погоды два взаимоисключающих события: "будет дождь" и "дождя не будет" и присвоить им некоторые ранги, то сумма этих рангов необязательно будет равна 1 (но если равенство все-таки есть, то нечеткое множество считается нормированным). Значения функции принадлежности М(х) могут быть взяты только из априорных знаний, интуиции (опыта), опроса экспертов.

В нечеткой логике вводится понятие лингвистической переменной, значениями которой являются не числа, а слова естественного языка, называемые термами. Например, в случае управления мобильным роботом (например роботом-пылесосом), задачей которого является объезд помех, можно ввести две лингвистические переменные: ДИСТАНЦИЯ (расстояние от робота до помехи) и НАПРАВЛЕНИЕ (угол между продольной осью робота и направлением на помеху). Рассмотрим лингвистическую переменную ДИСТАНЦИЯ. Значениями ее можно определить термы ДАЛЕКО, СРЕДНЯЯ, БЛИЗКО и ОЧЕНЬ БЛИЗКО. Для физической реализации лингвистической переменной необходимо определить точные физические значения термов этой переменной. Пусть переменная ДИСТАНЦИЯ может принимать любое значение из диапазона от нуля до бесконечности.

Согласно положениям теории нечетких множеств, в таком случае каждому значению расстояния из указанного диапазона может быть поставлено в соответствие некоторое число от нуля до единицы, которое определяет степень принадлежности данного физического расстояния (допустим 40 см) к тому или иному терму лингвистической переменной ДИСТАНЦИЯ. Степень принадлежности определяется так называемой функцией принадлежности M(d), где d — расстояние до помехи. В нашем случае расстоянию 40 см можно задать степень принадлежности к терму ОЧЕНЬ БЛИЗКО, равную 0,7, а к терму БЛИЗКО — 0,3 (см. рис. 6.16). В каждом конкретном случае определение степени принадлежности дается экспертами, разрабатывающими систему управления. Переменной НАПРАВЛЕНИЕ, которая может принимать значения в диапазоне от 0 до 360 °, зададим термы ЛЕВОЕ, ПРЯМО И ПРАВОЕ. Теперь необходимо задать выходные переменные. В рассматриваемом примере достаточно одной переменной, которая будет называться РУЛЕВОЙ УГОЛ. Она может содержать термы: РЕЗКО ВЛЕВО, ВЛЕВО, ПРЯМО, ВПРАВО, РЕЗКО ВПРАВО.

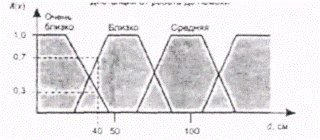
Рис. 6.16. Лингвистическая переменная и функция принадлежности.

Связь между входом и выходом фиксируется в таблице нечетких правил (табл. 6.1).

Таблица.6.1. Таблица нечетких правил для мобильного ообота

Каждая запись в данной таблице соответствует своему нечеткому правилу, например: "Если ДИСТАНЦИЯ БЛИЗКО и НАПРАВЛЕНИЕ ПРАВОЕ, тогда РУЛЕВОЙ УГОЛ РЕЗКО ВЛЕВО". Таким образом, мобильный робот с нечеткой логикой будет работать по следующему принципу: данные с сенсоров о расстоянии до помехи и направлении на нее будут фаззифицированы, обработаны согласно табличным правилам, дефаззифицированы, и полученные данные в виде управляющих сигналов поступят на привод робота.

Общая структура нечеткого микроконтроллера

Общая структура микроконтроллера, использующего нечеткую логику, показана на рис. 6.17. Она содержит в своем составе следующие составные части: блок фаззификации; базу знаний; блок решений; блок дефаззификации. Блок фаззификации преобразует четкие ("crisp") величины, измеренные на выходе объекта управления, в нечеткие величины, описываемые лингвистическими переменными в базе знаний. Блок решений использует нечеткие условные ("if — then") правила, заложенные в базе знаний, для преобразования нечетких входных данных в требуемые управляющие воздействия, которые носят также нечеткий характер. Блок дефаззификации преобразует нечеткие данные с выхода блока решений в четкую величину, которая используется для управления объектом.

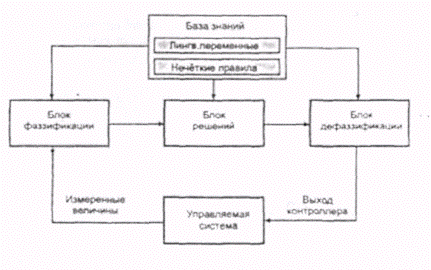
Рис. 6.17. Общая структура не четкого микроконтроллера.

В качестве микроконтроллеров, поддерживающих нечеткую логику, можно назвать 68HCI 1, 68НС12 фирмы Motorola, MC8-96 фирмы Intel, a также некоторые другие. Параллельно с развитием соответствующей элементной базы развиваются и инструменты программирования, которые позволяют как моделировать систему управления с нечеткой логикой, так и получать машинные коды, использующиеся впоследствии в "железе". Fuzzy Logic в стиральной машине.

На рис. 6.18 показана схема микроконтроллера системы Fuzzy Logic, управляющей работой стиральной машины. На вход микропроцессора поступает информация о степени загрязнения белья и типе загрязнения. Выходным параметром является время стирки.

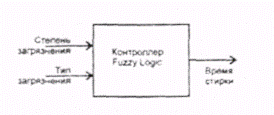
Рис. 6.18. Схема микроконтроллера системы Fuzzy Logic, управляющей работой стиральной машины.

Оба входных параметра получаются от одного оптического датчика прозрачности моющего раствора в баке стиральной машины см. рис. 6.19.

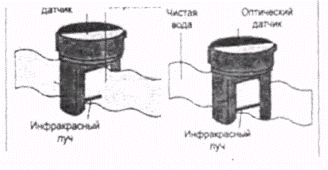
Рис. 6.19. Оптический датчик прозрачности раствора

О степени загрязнения можно судить по прозрачности моющего раствора: чем ниже загрязнение белья, тем прозрачнее вода. Первым входным параметром является "ПРОЗРАЧНОСТЬ РАСТВОРА". О типе загрязнения можно судить по скорости изменения прозрачности раствора (или, иными словами, по времени его насыщения): жирные загрязнения малорастворимы в воде и их концентрация в растворе медленнее выходит на уровень насыщения. Загрязнения низкой жирности растворяются лучше, и раствор в баке стиральной машины скорее становится насыщенным, вторым входным параметром здесь является "ВРЕМЯ НАСЫЩЕНИЯ РАСТВОРА".

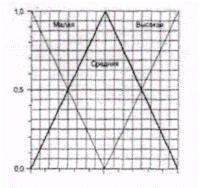
Таким образом, можно построить две функции принадлежности: в одном случае аргументом является степень загрязнения белья (рис. 6.20), в другом — тип загрязнения (рис. 6.21). В качестве диапазона изменения аргумента принимается интервал значений от 0 до 100. Значение выходного параметра "ВРЕМЯ СТИРКИ" (в данном случае это четкая величина, измеряемая в минутах) определяется с помощью набора нечетких правил "если... то", например: "Если ПРОЗРАЧНОСТЬ РАСТВОРА НИЗКА и ВРЕМЯ НАСЫЩЕНИЯ РАСТВОРА ВЕЛИКО, то ВРЕМЯ СТИРКИ ВЕЛИКО", или, что то же самое: "Если степень загрязнения высока и загрязнение жирное, то время стирки велико".

.•

Р. ис. 6.20. Функция принадлежности для аргумента "степень загрязнения".

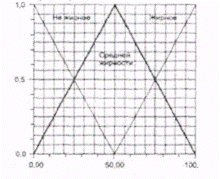
Рис. 6.21. Функция принадлежности для аргумента "тип загрязнения".

В данном примере, поясняющем принцип построения системы Fuzzy Logic, которая управляет стиральной машиной, рассматривался только один выходной параметр — "ВРЕМЯ СТИРКИ". Следуя тому же принципу, в реальных системах управления рассматриваются и другие выходные параметры, например, "УРОВЕНЬ ВОДЫ", "СКОРОСТЬ ВРАЩЕНИЯ ПРИ ОТЖИМЕ" и т.д., а среди входных параметров, кроме рассмотренных в данном примере, фигурируют также "ЖЕСТКОСТЬ ВОДЫ", "ЗАГРУЗКА БЕЛЬЯ", "ТИП БЕЛЬЯ". Набор нечетких правил в этом случае представляет многопараметрическую таблицу, согласно которой происходит принятие решения (рис. 6.22).

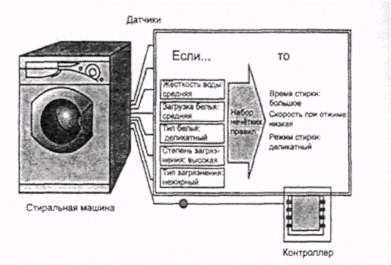
Рис. 6.22. Принятие решения системой управления по набору значений входных параметров.

Число возможных вариантов программы стирки при этом исчисляется многими сотнями, в чем и выражается качественное отличие стиральных машин с системой управления Fuzzy Logic от машин с электромеханической системой управления.