Проблематика и актуальность процессов транспорта носителей заряда в наноразмерных структурах
Значительный фронт современных научных и прикладных работ в направлении наноинженерии прямым или косвенным образом связаны с проблематикой создания перспективных высокопроизводительных (быстродействие, объем памяти, массово-габаритные параметры) вычислительных систем, обладающих чрезвычайно высокой степенью интеграции элементов (степень интеграции элементов – количество элементов конструкций, содержащихся в единице объема изделия). В табл. 2.1 представлены сведения о реальной и прогнозируемой динамике повышения степени интеграции элементов в вычислительных системах.
Т а б л и ц а 2.1. Динамика уменьшения размеров элементов конструкций
электронных устройств в вычислительных системах
| Год выпуска изделия | Степень интеграции Элемент / мм3 | Минимальный размер элемента, мкм | Допуск на изготовление, мкм |
| 10-2 (биполярный транзистор) | 3∙103 | > 10 | |
| 0.1 – 1.0 (микросборка элементов) | 103 | 5 – 10 | |
| 103 (ИС на биполярных структурах) | 102 | 2 – 5 | |
| 106 (ИС на МОП структурах) | 2 – 10 | 0.2 – 1.0 | |
| 109 (СБИС – 1е поколение) | 0.5 – 1.0 | 0.05 | |
| 1012 (СБИС – 2е поколение) | 10-1 | 10-2 | |
| 2020-2030 | 1014 – 1015 (прогноз) | 10-2 | 10-3 |
| Технология атомной сборки | 1019 – 1020 (без учета элементов коммутации) | 10-4 | Теоретический предел атомных технологий |
Примечание: ИС – «интегральная схема»; СБИС – «сверхбольшая интегральная схема»; МОП – структура типа «металл – окисел – полупроводник».
Согласно данным табл. 2.1, в этом научно-техническом направлении можно говорить о вхождении в область наноразмерных масштабов уже с 2000 г., по крайней мере в части обеспечения необходимых допусков на изготовление индивидуальных элементов конструкций вычислительных систем.
Столь малые размеры элементов конструкций современных и перспективных устройств электронной техники накладывают определенную специфику на процессы электропроводности в конструкционных материалах, применяемых при создании этих устройств. В частности, представляется весьма проблематичным использование в физико-технической практике традиционных и широко используемых теоретических моделей и подходов, основанных на макроскопических представлениях физики сплошных сред (термодинамика, статистическая и молекулярная физика).
Такое пристальное внимание к вопросам электропроводности указанных конструкционных материалов обусловлено их ключевой ролью при рассмотрении проблематики обеспечения функционального назначения изделий электронной техники. В общем случае при анализе электрической проводимости 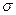 конструкционных материалов (в рамках макроскопического подхода) принято оперировать уравнением электропроводности вида
конструкционных материалов (в рамках макроскопического подхода) принято оперировать уравнением электропроводности вида
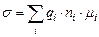 , ,
| (2.1) |
где i – индекс, характеризующий вклад в общую электропроводимость материала носителей зарядов iго типа; ni – концентрация носителей зарядов iго типа; 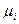 – подвижность носителей заряда iго типа; qi – модуль значения электрического заряда для индивидуального носителя заряда iго типа.
– подвижность носителей заряда iго типа; qi – модуль значения электрического заряда для индивидуального носителя заряда iго типа.
В случае макроскопических систем установление типа и величины qi индивидуальных носителей заряда, участвующих в процессе формирования электрического тока, не вызывает особых затруднений, поскольку они, как правило, известны для большинства используемых на практике конструкционных материалов. Для случая наноразмерных (хотя бы по одной пространственной координате) элементов конструкции, выполненных на основе материалов с электронным типом проводимости, этот аспект может существенно усложниться. Это связано со спецификой рассмотренных выше зонных энергетических диаграмм наноструктур, обусловленной наличием размерных ограничений на процессы движения микрочастиц и порой недостаточным (для реализации процесса векторизации энергии поступательного движения с помощью электрического поля) количеством свободных энергетических состояний. Вопрос о том, какие именно электроны из их общего количества в материале в этом случае можно отнести к носителям заряда, будет рассмотрен ниже. Этот важный для практики создания электронных устройств аспект самым непосредственным образом связан и с вопросами установления концентрации носителей заряда ni.
Более прозрачной представляется взаимосвязь подвижности носителей заряда 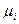 с пространственными ограничениями наноразмерных структур. Очевидным следствием ограничительных факторов является появление ярко выраженной анизотропии, т.е. зависимости свойств конструкционных материалов от рассматриваемого пространственного направления. Следует отметить, что фактор анизотропии наблюдается и у макроскопических материалов, однако в этих средах он проявляется, как правило, в весьма незначительных масштабах (за исключением узкого круга конструкционных материалов специального назначения: сегнетоэлектрики; ферромагнетики; композиты).
с пространственными ограничениями наноразмерных структур. Очевидным следствием ограничительных факторов является появление ярко выраженной анизотропии, т.е. зависимости свойств конструкционных материалов от рассматриваемого пространственного направления. Следует отметить, что фактор анизотропии наблюдается и у макроскопических материалов, однако в этих средах он проявляется, как правило, в весьма незначительных масштабах (за исключением узкого круга конструкционных материалов специального назначения: сегнетоэлектрики; ферромагнетики; композиты).
В разд. 1 показано определяющее влияние вида потенциальной функции электронов (т.е. конфигурация барьеров на пути следования микрочастиц) в атомных и регулярных (кристаллических) структурах на характер движения последних, которая (функция) формирует специфику процессов квантования элементарных энергетических состояний электронов. В рассматриваемых наноразмерных структурах потенциальная функция электронов может кардинально отличаться для различных пространственных направлений (в особенности для структур типа (1D) и (2D)), что, собственно, и составляет их главное отличие от макроскопических кристаллических структур. С учетом вышеизложенного фактора резкой анизотропии потенциальной функции электронов в наноразмерных структурах представляет интерес рассмотрение двух специфических вариантов процесса переноса носителей заряда:
· вдоль совокупности дискретных атомных потенциальных барьеров, т.е. в направлении отсутствия ограничений размерного характера;
· поперек совокупности дискретных атомных потенциальных барьеров, т.е. в направлении наличия ограничений размерного характера.
Первый, более простой вариант соответствует случаю практически свободного движения электрона (при большой длине цепочки атомов образующих наноразмерную структуру в направлении движения), при реализации которого волновой вектор k пробегает непрерывный ряд значений в диапазоне величин { 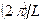 –
– 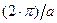 } (см. разд. 1.2.2, пункты д; е), где L – длина атомной цепочки. В этом варианте движение индивидуального электрона происходит путем последовательного чередования этапов свободного пролета на длине свободного пробега по пути следования электрона (обратить внимание на факт перекрытия волновых функций электрона согласно рис. 1.9) с этапами ее неупругого взаимодействия с атомами среды (электропроводимость по механизму «пролетного типа»). Этот тип движения аналогичен поведению индивидуального электрона в совершенных макроскопических кристаллических структурах, в которых процессы рассеяния векторизованного движения электронов происходят на дефектах точечного (вакансии, атомы внедрения и замещения) или линейного (краевые и винтовые дислокации) типа и на фононах (совокупности взаимосвязанных элементарных колебательных движений атомов, образующих кристаллическую структуру).
} (см. разд. 1.2.2, пункты д; е), где L – длина атомной цепочки. В этом варианте движение индивидуального электрона происходит путем последовательного чередования этапов свободного пролета на длине свободного пробега по пути следования электрона (обратить внимание на факт перекрытия волновых функций электрона согласно рис. 1.9) с этапами ее неупругого взаимодействия с атомами среды (электропроводимость по механизму «пролетного типа»). Этот тип движения аналогичен поведению индивидуального электрона в совершенных макроскопических кристаллических структурах, в которых процессы рассеяния векторизованного движения электронов происходят на дефектах точечного (вакансии, атомы внедрения и замещения) или линейного (краевые и винтовые дислокации) типа и на фононах (совокупности взаимосвязанных элементарных колебательных движений атомов, образующих кристаллическую структуру).
Второй, более сложный для анализа вариант соответствует случаю жесткой локализации местонахождения электрона в ограниченной области пространства, которому можно поставить в соответствие дискретный набор волновых векторов k , т.е. дискретный спектр энергетических состояний (см. разд. 1.2.2, пункт г). В этом случае движение индивидуального электрона происходит в виде последовательности дискретных «прыжков» («переходов»), которые могут быть реализованы путем:
· преодоления максимальной высоты потенциального барьера при реализации элементарного акта движения, для чего индивидуальным электронам необходимо обладать энергией большей, чем высота барьера (электропроводимость по кативационному механизму «прыжкового типа»);
· своеобразного «просачивания» индивидуального электрона сквозь потенциальный барьер, исключая необходимость преодоления этого барьера по механизму прыжкового (см. предыдущий пункт) типа (электропроводимость по механизму «туннельного типа»).
Приведенная классификация в определенной мере, в общих чертах, прослеживает основополагающие принципы и методы анализа процессов электронного и ионного транспорта в наноразмерных кристаллических структурах.
Дата добавления: 2016-01-03; просмотров: 677;
