СИСТЕМЫ УРАВНЕНИЙ И ПАРАМЕТРОВ ЧЕТЫРЁХПОЛЮСНИКА

МЕТОД ЭКВИВАЛЕНТНОГО ЧЕТЫРЁХПОЛЮСНИКА

Исследование режима работы сложной электронной схемы часто сводится к установлению связи между токами и напряжениями двух ветвей этой схемы. Так как каждая ветвь присоединяется к остальной части схемы в двух узлах, то выделяется часть схемы с четырьмя зажимами (полюсами); причем к одной паре зажимов (входной) обычно присоединяется источник энергии (сигнала), а к другой (выходной) – приемник (нагрузка).

Часть электрической цепи произвольной конфигурации, имеющая две пары зажимов для присоединения источника и приемника энергии, называется четырехполюсником. Четырехполюсники делятся на активные и пассивные. Четырехполюсники, не содержащие в своем составе источников энергии, называются пассивными. Четырехполюсники, содержащие в своих ветвях источники энергии, называются активными.

СИСТЕМЫ УРАВНЕНИЙ И ПАРАМЕТРОВ ЧЕТЫРЁХПОЛЮСНИКА

Любой линейный четырехполюсник (рис.4.1) можно описать рядом уравнений, связывающих между собой токи и напряжения на входе и выходе четырехполюсника

Рисунок 4.1

В общем случае для ч.п. можно записать 6 существенно разных вариантов уравнений. Наибольшее распространение получили уравнения, связывающие «вход с выходом», которые обычно называют основными уравнениями четырехполюсника. При этом в качестве независимых переменных выбирают величины 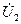и :

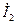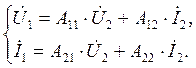(4.1)

Уравнения, связывающие напряжения на входе и выходе ч.п. с соответствующими токами, записываются в следующем виде:

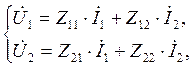
(4.2)

а уравнения, в которых в качестве независимых переменных принимаются напряжения 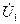и 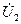, в виде:

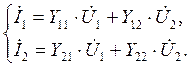(4.3)

Так называемые смешанные или «гибридные» уравнения записываются в виде:

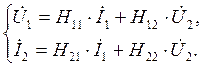(4.4)

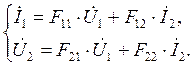(4.5)

Наконец, уравнения, в которых в качестве независимых переменных принимаются напряжение 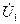и ток 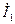на входе четырехполюсника, имеют вид:

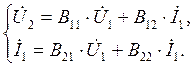(4.6)

В общем случае коэффициенты A, Z, Y, H, F и В являются комплексными. В тех случаях, когда они являются вещественными (что имеет место для большинства линейных электронных цепей), их обозначают малыми буквами a, r, y, h, f и b.

В матричной форме уравнения (4.1)…(4.6) можно записать следующим образом:

; ;

; ;

; .

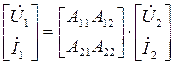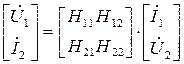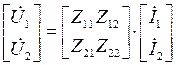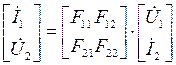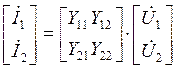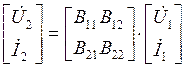В этих уравнениях квадратные матрицы, как и их элементы, являются параметрами четырехполюсника. Если для четырехполюсника известны (или получены) коэффициенты одной из систем уравнений (4.1)…(4.6), то коэффициенты любой другой системы уравнений можно получить путем несложного взаимного пересчета коэффициентов. В таблице 4.1 приведены некоторые формулы для взаимного пересчета одних коэффициентов уравнений (4.1)..(4.6) в другие (т.е. элементов матриц), где через |Y|, |Z|, |H| и т.д. обозначены определители соответствующих матриц.

В таблице 4.2 приведены соотношения между определителями матриц эквивалентных параметров, позволяющие осуществлять переход от определителя одной системы параметров к другой.

Таблица 4.1

От ® К К¯	[Z]	[Y]	[H]	…
[[Z]				…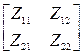
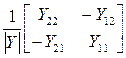
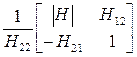
[[Y]				…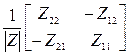
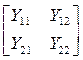
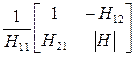
[[H]				…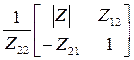
	…	…	…

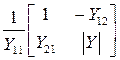
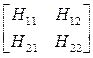
Таблица 4.2

От ®   К ¯	|Y|	|Z|	|H|	…
|Y|	|Y|			…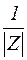
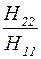
|Z|		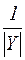|Z|		…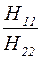
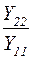
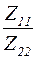
|H|			|H|	…
…	…	…	…

4.2 Z-ПАРАМЕТРЫ ЧЕТЫРЕХПОЛЮСНИКА. ОПРЕДЕЛЕНИЕ ВТОРИЧНЫХ ПАРАМЕТРОВ СХЕМ, ПРИВОДЯЩИХСЯ К ЧЕТЫРЕХПОЛЮСНИКАМ, ПО Z-ПАРАМЕТРАМ ЭКВИВАЛЕНТНОГО ЧЕТЫРЕХПОЛЮСНИКА

Если, как уже отмечалось ранее, в качестве независимых переменных выбрать ток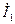и и 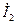, то для четырехполюсника можно записать следующие уравнения:

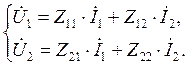(4.7)

Параметры четырехполюсника Z₁₁, Z₁₂, Z₂₁ и Z₂₂ имеют размерность сопротивления, т.к. умножение каждого из них на ток в (4.7) дает напряжение. Двузначные индексы коэффициентов уравнений (параметров) указывают на то, какую именно пару величин связывает данный параметр:

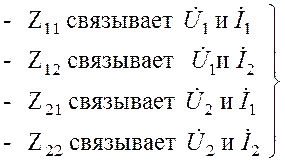
В каждом случае здесь первый индекс указывает на зависимую переменную, а второй – на независимую.

Уравнения (4.7) справедливы для всех значений независимых переменных. Поэтому они справедливы также и в тех случаях, когда ток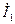и и 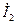равны нулю. Предположим, что ток 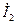=0, что может иметь место лишь, когда выходные зажимы четырехполюсника разомкнуты (режим холостого хода по выходу). Уравнения (4.7) при этом приобретают вид:

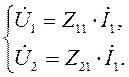
Откуда получаем:

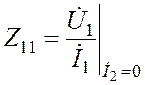
	-входное сопротивление четырехполюсника в режиме идеального холостого хода его выходной цепи;
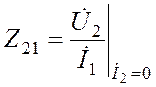
	-сопротивление прямой связи (определяет э.д.с. на выходе вторичной цепи четырехполюсника в режиме идеального холостого хода по выходу).

Аналогично, предполагая режим идеального холостого хода по входной цепи четырехполюсника, получаем:

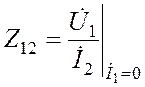
	-сопротивление обратной связи;
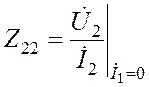
	-выходное сопротивление четырехполюсника в режиме идеального холостого хода в его входной цепи (в этом режиме э.д.с. вторичной цепи 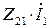равна 0, что дает основание определять Z22 как выходное сопротивление четырехполюсника).

Одна из задач, часто встречающихся при анализе электронных схем, заключается в определении вторичных выходных параметров схемы используя параметры эквивалентного четырехполюсника, к выходу которого подключена нагрузка Z_н, а к входной цепи подключен генератор 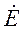с внутренним сопротивлением Z_вн (рис. 4.2):

Рисунок 4.2.

Так, представив 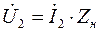, и подставляя 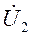в уравнения (4.7), получаем:

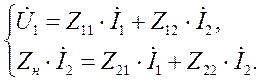(4.8)

Решив эту систему относительно 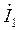в результате получаем:

.

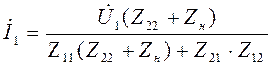Откуда:

.

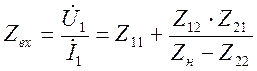Решив систему (4.8) относительно 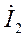, имеем:

.

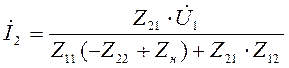Откуда находим проводимость передачи:

,

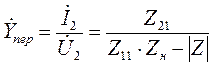где |Z|=det[Z_ij]=Z₁₁×Z₂₂ - Z₂₁×Z₁₂ – определитель матрицы Z-параметров.

Поскольку 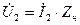, используя уравнение для 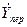можно определить коэффициент передачи четырехполюсника по напряжению:

.

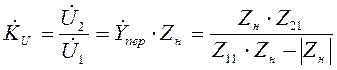Полученные выше зависимости известны в специальной литературе под названием общего решения четырехполюсника через Z-параметры.

Аналогичным образом можно получить еще ряд общих решений, например:

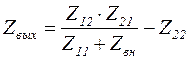- выходное сопротивление четырехполюсника;

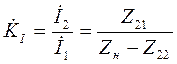- коэффициент передачи по току.

Таким образом, имея матрицу Z-параметров четырехполюсника, эквивалентного анализируемой схеме, можно с помощью приведенных выше формул определять вторичные выходные параметры схемы.

4.3 Y-ПАРАМЕТРЫ ЧЕТЫРЕХПОЛЮСНИКА

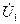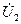Независимые переменные и . Для четырехполюсника можно записать уравнения:

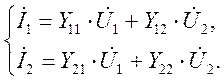(4.9)

Условия определения параметров – короткое замыкание по входной и выходной цепи. При этом:

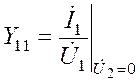
	-входная проводимость четырехполюсника в режиме короткого замыкания его выходной цепи;
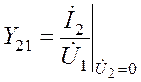
	-проводимость прямой связи (коэффициент пропорциональности в режиме короткого замыкания вторичной цепи, устанавливающий связь между напряжением в первичной цепи и током во вторичной цепи).
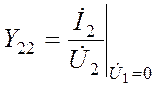
	-проводимость выходной цепи четырехполюсника в режиме короткого замыкания по переменному току в его входной цепи.
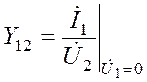
	-проводимость обратной связи.

Как и случае Z-параметров могут быть получены выражения для расчета вторичных выходных параметров схемы с использованием Y-параметров эквивалентного четырехполюсника (получить самостоятельно выражения для , , ).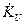

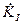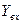4.4 H-ПАРАМЕТРЫ ЧЕТЫРЕХПОЛЮСНИКА

Выбор независимых переменных соответствует принципу: входные величины предшествуют выходным, а напряжения – токам. Независимыми переменными являются 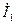и 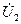. Основные уравнения имеют вид:

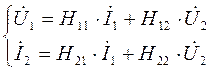(4.10)

Для определения H-параметров надо обеспечить либо холостой ход по входной цепи, либо короткое замыкание в выходной цепи.

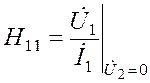
	-входное сопротивление четырехполюсника в режиме короткого замыкания по переменному току в его выходной цепи;
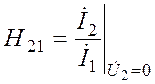
	-коэффициент передачи по току;
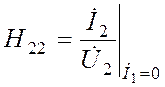
	-выходная проводимость четырехполюсника в режиме холостого хода в его входной цепи;
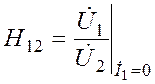
	-безразмерный коэффициент обратной связи.

Как и случае Z-параметров могут быть получены выражения для расчета вторичных выходных параметров схемы с использованием H-параметров эквивалентного четырехполюсника (получить самостоятельно выражения для , , ).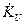

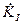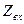Примечания:

- методика получения соответствующих зависимостей для других систем параметров четырехполюсника аналогична рассмотренной в р. 4.2, 4.3 и 4.4;

- в таблице 4.3 приведены зависимости для определения некоторых вторичных выходных параметров схемы с использованием Z,Y,H-параметров эквивалентного четырехполюсника;

- более полная таблица есть в кн. «Сигорский В.П., Петренко А.И. Основы теории электронных схем. Киев, 1967.»

Таблица 4.3

Параметр	Обозначение	Система параметров
[H]	[Y]	[Z]
Входное сопротивление (проводимость)	Wвх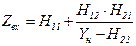
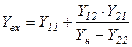
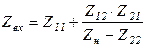
Выходное сопротивление (проводимость)	Wвых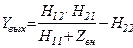
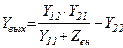
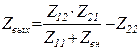
Коэффициент передачи по напряжению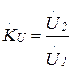
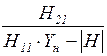
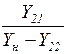
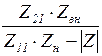
Коэффициент передачи по току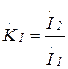
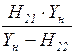
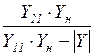
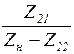
Проводимость передачи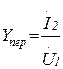
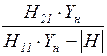
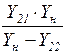
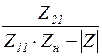
Сопротивление передачи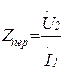

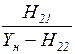
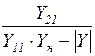
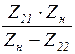
Примечания: 1. Параметры четырехполюсника определены для Y_н=0 и Y_вн=0 .

2. ,

.

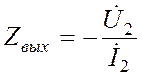4.5 ОСНОВНЫЕ СОЕДИНЕНИЯ ЧЕТЫРЕХПОЛЮСНИКОВ

Любая сложная схема, приводимая к виду четырехполюсника, может в конечном итоге рассматриваться как сочетание (соединение) некоторых простейших (элементарных) четырехполюсников. Как правило, параметры таких четырехполюсников известны либо определяются сравнительно просто. Анализ (расчет) такой схемы сводится к:

а) выделению в схеме входных и выходных зажимов и представлению её эквивалентным четырехполюсником;

б) представлению эквивалентного четырехполюсника соединением простейших четырехполюсников;

в) записи (определению) нужных матриц параметров этих четырехполюсников (их можно найти так же в заранее составленных специальных таблицах);

г) получение матриц параметров эквивалентного четырехполюсника на основе матриц простейших (элементарных) четырехполюсников с учетом различных способов их соединения;

д) определению интересующих вторичных выходных параметров схемы, используя матрицу параметров эквивалентного четырехполюсника.

При выполнении описанной процедуры используют несколько видов соединений простейших (элементарных) четырехполюсников. К основным соединениям относятся последовательное (каскадное, цепочное), параллельное, этажное, этажно-параллельное, параллельно-этажное. Ниже приведены примеры основных соединений двух четырехполюсников:

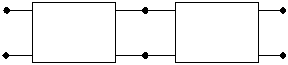
	- Последовательное
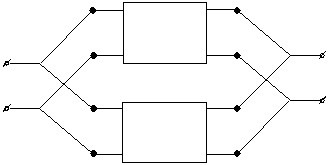
	- Параллельное
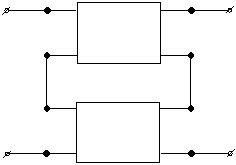
	-Этажное
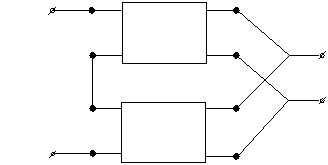
	- Этажно-параллельное
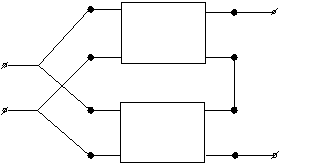
	- Параллельно-этажное

4.6 ОДНОРОДНЫЕ СОЕДИНЕНИЯ ЧЕТЫРЕХПОЛЮСНИКОВ

Если в составе эквивалентного четырехполюсника имеют место основные соединения одного вида элементарных четырехполюсников, то такие соединения называют однородными.

4.6.1 При последовательном соединении двух четырехполюсников внешние токи и напряжения связаны между собой зависимостями, указанными на рис. 4.3:

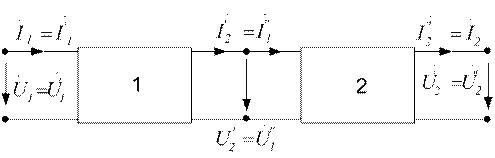
Рисунок 4.3

Для данного вида соединения можно записать:

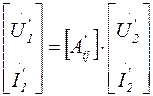и ,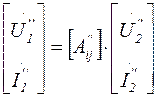

где 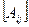- матрица А-параметров четырехполюсника.

Учитывая, что:

= , = , = ,

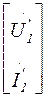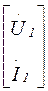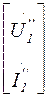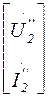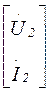получаем уравнение для эквивалентного четырехполюсника:

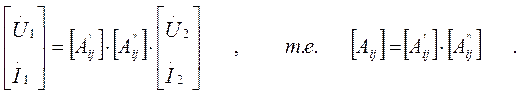
Таким образом, матрица А-параметров эквивалентного четырехполюсника равна произведению матриц А-параметров последовательно соединенных четырехполюсников. При последовательном соединении нескольких четырехполюсников их матрицы А-параметров перемножаются в той последовательности, в какой следуют четырехполюсники:

.

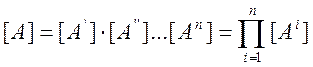4.6.2 Несложно показать, что при параллельном соединении четырехполюсников их матрицы Y-параметров суммируются, т.е.

.

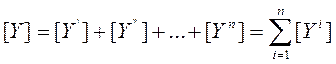При выводе последней формулы следует иметь в виду, что при параллельном соединении внешние напряжения являются общими для всех четырехполюсников, а внешние токи суммируются.

Аналогичные рассуждения приводят к следующим результатам:

- при этажном соединении четырехполюсников суммируются их матрицы Z-параметров;

- при этажно-параллельном соединении – суммируются матрицы H-параметров;

- при параллельно-этажном – суммируются матрицы F-параметров.

4.6.3 Основные виды соединений и формулы расчета параметров эквивалентного четырехполюсника приведены в таблице 4.4

Таблица 4.4

Соединение	Формула
Последовательное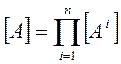
Параллельное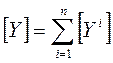
Этажное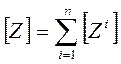
Этажно-параллельное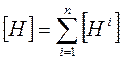
Параллельно-этажное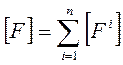

4.7 ПРИМЕНЕНИЕ МЕТОДА ЧЕТЫРЕХПОЛЮСНИКА

К АНАЛИЗУ ЭЛЕКТРОННЫХ СХЕМ

В таблице 4.4 приведены формулы для определения матриц параметров эквивалентного четырехполюсника, содержащего однородные соединения, т.е. соединения одного вида (последовательное, параллельное и т.д.). В общем случае для представления реальной схемы сочетанием простых четырехполюсников может потребоваться не один, а несколько видов соединений в пределах схемы. Такие соединения называют неоднородными. Основная особенность расчета неоднородных соединений состоит в необходимости переходов от одной системы параметров четырехполюсника к другой с помощью зависимостей между системами параметров (см. р. 4.1).

Порядок анализа (расчета) схемы при использовании метода четырехполюсника рассмотрим на примере:

Пример 4.1 Получить матрицу параметров четырехполюсника, эквивалентного схеме усилителя, приведеной на рис.4.4 (приведена рабочая схема – схема для переменных составляющих сигнала).

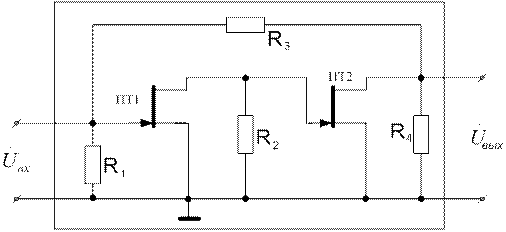
Рисунок 4.4

1) Представляем эквивалентный четырехполюсник (он обведен пунктиром на рис. 4.4) в виде соединений простейших четырехполюсников – рис. 4.5 Здесь четырехполюсники 1, 2, 3 и 4 соединены последовательно, а 5-й четырехполюсник – параллельно им.

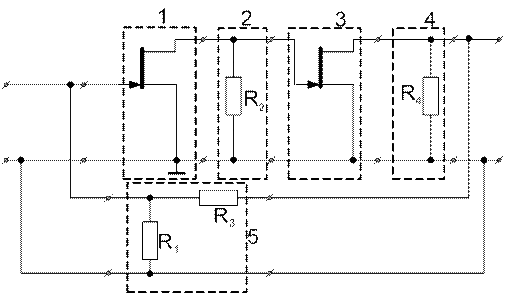
Рисунок 4.5

2) Определяем матрицу А-параметров четырехполюсника, эквивалентного последовательно соединенным четырехполюсникам 1 – 4:

[A]^(1-4)=[A]⁽¹⁾·[A]⁽²⁾·[A]⁽³⁾·[A]⁽⁴⁾.

По справочнику находим, что матрица А-параметров для одинаковых четырехполюсников 1 и 3 (ПТ) имеет вид:

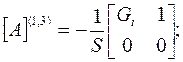
матрица А-параметров для одинаковых четырехполюсников 2 и 4 имеет вид (таблица 4.6):

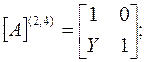
Перемножив матрицы А-параметров четырехполюсников 1-4, получаем матрицу А-параметров четырехполюсника, эквивалентного последовательно включенным простейшим четырехполюсникам 1-4. Она должна быть преобразована к виду:

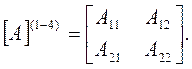
3) Переходим от матрицы А-параметров этого четырехполюсника к матрице Y-параметров, используя следующую формулу перехода:

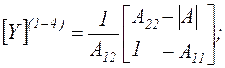
где |A|=det[A]^(1-4).

4) Записываем матрицу Y-параметров для параллельно соединенных четырехполюсников (1-4) и 5:

[Y]=[Y]^(1-4)+[Y]⁽⁵⁾,

где 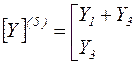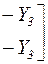- из справочника.

Матрица [Y] – искомая матрица четырехполюсника, эквивалентного заданной схеме.

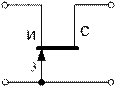
Матрицы параметров четырёхполюсников, представляющих полевые транзисторы на низкой частоте, без токов затвора приведены в таблице 4.5. Матрицы параметров четырехполюсников, составленных из пассивных элементов приведены в таблице 4.6.

Таблица 4.5

Схема	[Y]	[H]	[F]	[A]
		–
		–

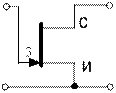
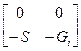
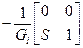
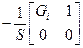
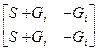
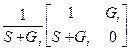
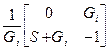
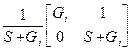
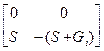
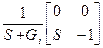
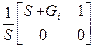
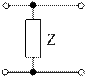
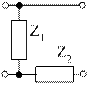
Таблица 4.6

Схема	[Y]	[Z]	[H]	[F]	[A]
	—	—
		—
	—

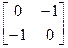
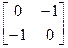
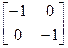
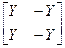
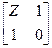
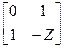
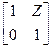
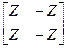
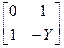
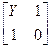
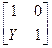
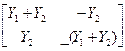
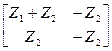
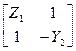
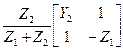
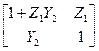
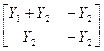
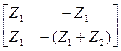
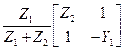
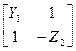
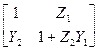
Пример 4.2 Пользуясь методом четырехполюсника, получить выражение для определения коэффициента передачи по напряжению 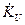истокового повторителя, схема которого приведена на рис. 4.6. Повторитель работает в диапазоне высоких частот, где реактивные сопротивления емкостей С_1,С₂ и С₃ малы.

1) На рис. 4.7а приведена рабочая схема повторителя – схема для переменных составляющих сигнала. Представление повторителя соединением простейших четырехполюсников показано на рис. 4.7б. Здесь четырехполюсники 1 и 2 соединены последовательно, а четырехполюсник 3 – параллельно им.

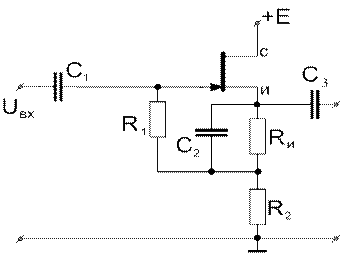
Рисунок 4.6

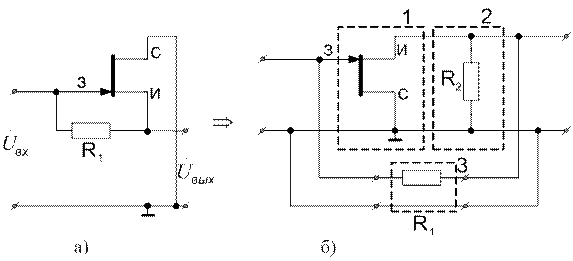
Рисунок 4.7

2) Определяем матрицу А-параметров четырехполюсника, эквивалентного последовательно соединенным четырехполюсникам 1 и 2:

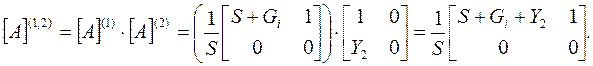
3) Переходим от матрицы А-параметров к матрице Y-параметров:

,

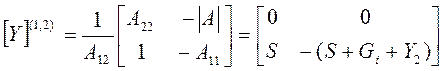где , , .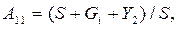

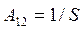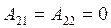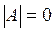4) Определяем матрицу Y-параметров истокового повторителя, как параллельно соединенных четырехполюсников (1,2) и 3:

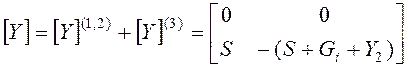
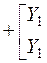
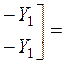
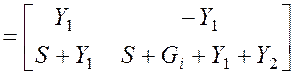
5) Коэффициент передачи схемы по напряжению определяем по формуле (см. табл. 4.3):

.

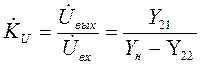Т.к. в схеме рис. 4.7 Y_н=0 (R_н®¥), то

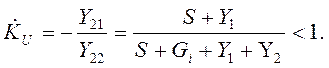
6) Задачу можно решить несколько иначе, если рассматривать резистор R₂ как нагрузку эквивалентного четырехполюсника:

Матрица Y-параметров параллельно соединенных четырехполюсников 1 и 2 имеет вид:

,

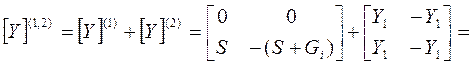
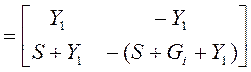где = .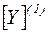

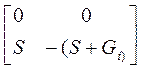Тогда: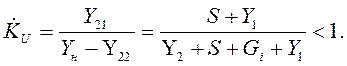

4.8 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ЧЕТЫРЕХПОЛЮСНИКОВ

4.8.1 Параметры эквивалентного четырехполюсника, к которому приводится схема с двумя входными зажимами и двумя выходными, можно выразить через определитель и алгебраические дополнения матрицы сопротивления (или проводимости) анализируемой схемы. Действительно, уравнения для внешних токов схемы, приводимой к виду четырехполюсника, имеют вид:

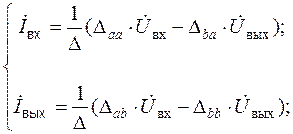
(4.11)

где Δ – определитель матрицы сопротивления схемы; Δ_ba, Δ_ab, Δ_aa, Δ_bb – алгебраические дополнения определителя; 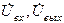- соответственно входное и выходное напряжения схемы.

Сравним (4.11) с системой уравнений для четырехполюсника в Y-параметрах:

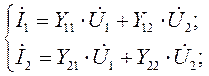(4.12)

где 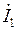, 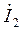- токи на входе и выходе четырехполюсника; 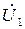, 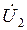- напряжения, соответственно, на входе и выходе четырехполюсника.

Считая, что 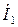= 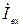, 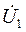= 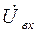, 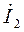= 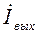, 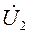= 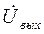, можно записать:

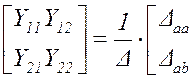
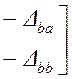. (4.13)

Уравнение (4.13) позволяет оценить Y-параметры эквивалентного четырехполюсника, используя определитель и алгебраическое дополнение матрицы сопротивления схемы.

Если уравнения системы (4.11) решить относительно 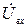и :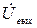

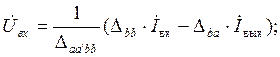
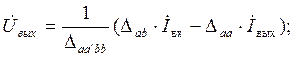
и сравнить полученные уравнения с системой уравнений для четырехполюсника в Z-параметрах:

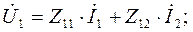
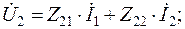
то можно установить что:

.

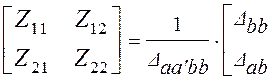
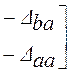Аналогично получаются и другие соотношения, приведенные ниже в таблице 4.7:

Таблица 4.7

Матрица параметров четырехполюсника	Выражение через определитель и алгебраические дополнения
Матрица сопротивления	Матрица проводимости

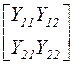
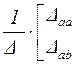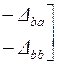
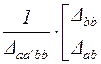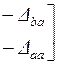
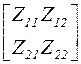
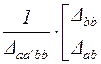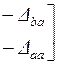
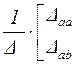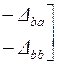
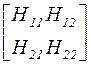
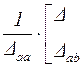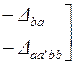
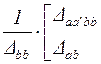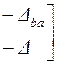
4.8.2 Если структура четырехполюсника неизвестна, то его параметры можно определить экспериментально. Для этого необходимо поочередно на входе и выходе четырехполюсника воспроизвести режимы холостого хода ( 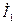=0, 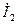=0) и короткого замыкания ( 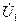=0, 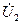=0) и определить отношения соответствующих токов и напряжений.

Если параметры четырехполюсника измеряются на переменном токе и необходимо обеспечить при этом неизменность режима работы четырехполюсника на постоянном токе, то режим короткого замыкания соответствует закорачиванию большой емкостью входных или выходных зажимов четырехполюсника, а режим холостого хода – последовательному включению в цепь соответствующих зажимов большой индуктивности. Режим работы четырехполюсника по постоянному току при этом не изменится.

При экспериментальном определении параметров четырехполюсника следует иметь в виду важное обстоятельство: при воспроизведении режимов холостого хода и короткого замыкания на входе четырехполюсника и подаче на его выход задающего напряжения, ток в выходной цепи четырехполюсника (ток 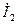) будет иметь направление, противоположное принятому на рис. 4.1. Поэтому параметры четырехполюсника, стоящие коэффициентами при токе 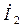в его уравнениях, будут получены со знаком «-».