Основные процессы преобразования измерительных сигналов

В основе исследования электрических сигналов лежит широко используемый принцип суперпозиции (наложения), который упрощенно можно выразить следующим образом: в линейной системе действие суммы причин равно сумме действий, вызываемых каждой причиной, отдельно взятой. Существуют два равноценных подхода к исследованию свойств систем – временной, при котором процесс описывается функцией времени, и спектральный (частотный), при котором процесс описывается заданием комплексного спектра, являющегося функцией частоты.

Наиболее часто в качестве ортогональных функций применяют тригонометрические функции, образующие обычный ряд Фурье. И в этом случае любой периодический сигнал f(t) можно представить на интервале рядом элементарных сигналов:

,

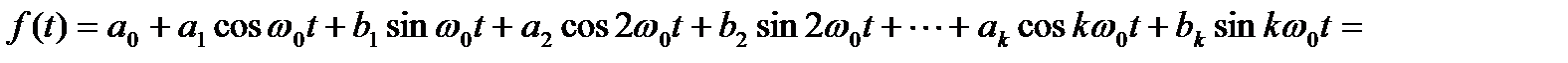
где - постоянная составляющая; 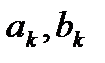- коэффициенты k-й гармоники;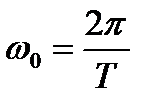

– круговая частота; T –период сигнала f(t); k – целые числа.

Коэффициенты ряда Фурье определяются по формулам

; ; .

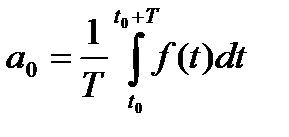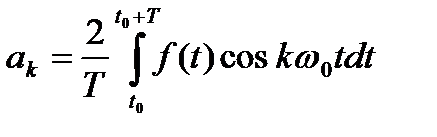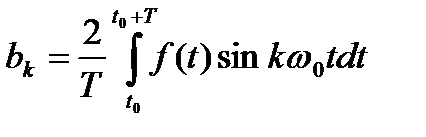Тригонометрический ряд Фурье применяют также в следующей форме:

, (1.1)

где А₀ –постоянная составляющая, 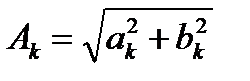; ; 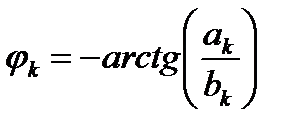k =1,2,3… .