Логика сложных процентов
В одной из книг Якова Исидоровича Перельмана есть такой сюжет.
Человек кладет в банк 1000 руб. под 100 % годовых. Это значит, что при хранении вклада в течение года его величина вырастает на 100 % первоначального значения, т. е. на 1000 руб. и если вкладчик предполагает хранить свои деньги в банке ровно в течение года, он сможет в конце этого периода получить 1000 + 1000 = 2000 руб.
Правила хранения таковы, что вкладчик может в любой момент получить свои деньги.
Проценты простые, т.е. приращение вклада пропорционально времени хранения. Если вкладчик захочет получить свои деньги через два года, то его вклад увеличится на 2000 руб. ему будет причитаться всего 3000 руб., а если он захочет снять свои деньги через полгода, то вклад увеличится на 500 руб. и составит всего 1500 руб.
Но вкладчик все-таки хочет хранить деньги в банке ровно год. И ему в голову приходит такая мысль: а что если через полгода ему переоформить вклад, т. е. как бы получить деньги и сразу же положить их снова храниться еще полгода? Сумма, выросшая за полгода, составит, как мы видели, 1500 руб. А если эти 1500 руб оставить теперь еще на полгода в банке, то сумма увеличится еще на 1500·1/2 = 750 руб. и составит 2250 руб. Это больше, чем та сумма, которая получилась бы без переоформления, так что такая операция вкладчику, безусловно, выгодна.
Читатель, возможно, заметил, что мы могли бы все расчеты выполнить проще. За первые полгода вложенная сумма возрастает в 1 + 1/2 =l.5 раза. За вторые полгода уже новая сумма возрастает в 1.5 раза, так что всего в конце года вкладчик должен получить:
1000(1 + 1/2)2 = 2250 руб.
Но вернемся к нашему вкладчику. Он продолжает свои размышления: а если переоформлять вклад через каждый квартал? Тогда в конце концов получится:
1000(1+1/4)4 = 2441.41 руб.,
т. е. еще больше! (Если вы захотели проверить результат, учтите, что мы округляем результат до целых копеек).
Легко сообразить, что, переоформляя вклад N раз в течение года, вкладчик в конце концов получит:
1000 (l+1/N)N руб.
При ежемесячном переоформлении вклада сумма составит 2613.04 руб., а при ежедневном, считая, что банк работает без выходных, — 2714.57 руб. Как видим, переход от N = 12 к N = 365 не очень сильно увеличил сумму — всего на 101 руб. с копейками, — так что выигрыш едва ли стоит ежедневных хлопот с переоформлением.
Но в мысленном эксперименте мы можем пойти еще дальше: а что произойдет при бесконечно частом переоформлении? Величина (1+1/N)N, как известно из курса математики, при N → + стремится к пределу, равному е ≈ 2.718 281 8... Таким образом, если переоформление вклада превратится в непрерывный процесс, то при 100 % годовых вкладчик к концу года сможет получить в банке 1000е ≈ 2718.28 руб., т. е. доход на вложенную 1000 руб. составит 2718.28 – 1000 = 1718.28 руб.
Теперь мы отойдем от перельмановского сюжета и попытаемся найти ответы на некоторые вопросы. Вполне ли разумны рассмотренные нами правила хранения вклада?
Нельзя ли их улучшить? И что означает цифра “100 % годовых”, если при соблюдении всех правил вкладчик может получить в течение года доход почти 172 %?
Чем неудачны правила, предложенные банком? Они побуждают вкладчика часто переоформлять свой вклад. При этом он не получает и не вкладывает никаких денег. Как будто ничего не происходит — а его доход увеличивается.
Банк, назначив ставку 100 % в год, должен быть готов за пользование вкладом в течение года заплатить без малого 172 % и при этом загрузить своих служащих бесполезной работой по переоформлению вкладов.
Можно, конечно, запретить вкладчику какое-то время совершать операции по своему вкладу или по крайней мере понижать процентную ставку, если вкладчик захочет воспользоваться своими деньгами в течение “запретного” периода. Можно ввести плату за переоформление. Можно не накапливать доход на счете вкладчика, а выплачивать ему причитающиеся суммы “непрерывно” (на практике — через короткие промежутки времени). Но мы рассмотрим другую возможность: попытаемся отказаться от простых процентов, т. е. от начисления дохода пропорционально сроку хранения вклада, и попробуем найти такую зависимость дохода от времени хранения вклада, которая избавила бы и вкладчика, и банк от перечисленных выше неудобств. Уязвимым местом первоначального правила начисления дохода было следующее обстоятельство: операции, не изменяющие в момент их совершения количества денег у каждой из сторон, тем не менее изменяли в конце концов доход вкладчика. Назовем такие операции фиктивными; попытаемся сконструировать правила таким образом, чтобы выполнение фиктивных операций не изменяло дохода вкладчика. Пусть v обозначает сумму, вносимую вкладчиком в момент t0; сумму, которую он получит в банке через некоторое время, в момент t1, обозначим w. Функция роста, связывающая эти величины:
w = F(v, t0, t1),
выражает количественную сторону правила начисления дохода. Для правила простых процентов, которое мы теперь ставим под сомнение, эта функция описывает линейную зависимость от времени хранения:
w = F(v, t0, t1),
выражает количественную сторону правила начисления дохода. Для правила простых процентов, которое мы теперь ставим под сомнение, эта функция описывает линейную зависимость от времени хранения:
| w = v[1 + (t0 – t1), |
где коэффициент определяется процентной ставкой.
Потребуем, чтобы функция роста обладала следующими тремя свойствами.
1. Стационарность: один и тот же по величине вклад при одной и той же продолжительности хранения дает одно и то же значение функции роста, независимо от момента вложения (рис. 4). Иными словами, значения функции роста должны зависеть только от разности Т = t0 – t1. Приняв это требование, мы можем записать функцию роста как w = F(v, T).
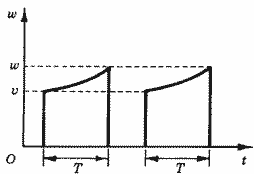
Рис. 4. Стационарность роста
2. Аддитивность: рост суммы вкладов равен сумме функций роста по каждому из вкладов в отдельности (рис. 5). Зафиксируем моменты внесения и получения вкладов и рассмотрим зависимость размера выплаты w только от величины первоначального вклада: w = G(v). Требование аддитивности означает выполнение равенства:
| G(x + y) = G(x) + G (y) (1) |
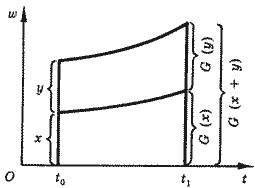
Рис. 5. Аддитивность роста
В чем смысл этого требования? Если бы при каких-нибудь значениях х и y имело бы место неравенство:
| G(x + y) < G(x) + G(y), |
то вкладчику было бы выгодно свой вклад v = х + y разделить на два вклада размером х и y. Но количество денег у вкладчика не зависит от того, сделает ли он один вклад размером 1000 руб. или разделит его на части размером 300 и 700 руб. Не зависит от этого и количество денег, поступающее в распоряжение банка, так что дробление вклада — фиктивная операция.
Если бы, напротив, имело место неравенство:
| G(x + y) > G(x) + G(y), |
вкладчик был бы заинтересован, например, объединиться с приятелем, договорившись о распределении дополнительного дохода. Но такое объединение — тоже фиктивная операция. Итак, мы признали требование (1) разумным. Но непрерывная функция, обладающая этим свойством — это прямая пропорциональность:
| G(v) = kv. |
Доказательство этого факта помещено в Математическом приложении VI. Вспомним, что функция G(v) описывает рост при фиксированных моментах t0 и t1. Если же эти моменты произвольны, то коэффициент k должен зависеть от t0 и t1, а поскольку мы приняли допущение о стационарности, коэффициент k должен зависеть от продолжительности хранения вклада. Таким образом, мы пришли к следующему результату: функция роста, отвечающая требованиям 1 и 2, должна иметь вид:
| F(v, T) = vk(T). (2) |
Функцию k(T) будем называть коэффициентом роста вклада.
3. Согласованность во времени. Пусть вклад v за время хранения вклада T1 возрастает до значения w1, а вклад w1 за последующий период хранения T2 возрастает до w2 (рис. 6).
Потребуем, чтобы за время хранения T1 + T2 первоначальный вклад v возрастал до того же самого значения w2. Иными словами, мы хотим, чтобы фиктивная операция переоформления вклада не изменяла дохода вкладчика.
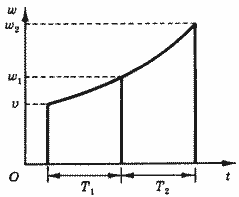
Рис. 6. Согласованность во времени
Из равенства (2) следует:
| w1 = vk(T) и w2 = w1k(T2) = vk(T1)k(T2). |
Мы требуем, чтобы выполнялось также равенство:
| w2 = vk(T1 + T2). |
Таким образом, коэффициент роста должен удовлетворяет условию:
| k(T1 + T2) = k(T1)k(T2). (3) |
Подобно тому как условию (1) соответствует только прямая пропорциональность, требованию (3), предъявляемому к коэффициенту роста, отвечает только показательная функция:
| k(T) = eρT. |
Коэффициент ρ показывает, с какой скоростью происходит рост вклада.
Таким образом, всем трем рассмотренным требованиям отвечает функция:
| w = vρT.. |
Заметим, что коэффициенту роста можно придать эквивалентную форму:
| k(T) = RT, (4) |
или:
| k(T) = (1+r)T, (5) |
полагая R = eρ, r = R – 1.
Теперь в нашем распоряжении имеются различные показатели, характеризующие скорость возрастания вклада. Между ними существует взаимно однозначная связь. В частности,
ρ = lnR = ln(1 + r).
Выясним, что показывает каждый из этих показателей.
Из равенства (4) видно, что при Т = 1, т. е. при хранении вклада в течение единицы времени (например, года), первоначальный вклад увеличивается в R раз, или возрастает на долю r своей первоначальной величины. Величина r100 % обычно называется процентной ставкой, а формула (5) — формулой сложных процентов. Будем считать, что вклад производится в момент t0 после чего доход начисляется непрерывно; будем рассматривать накопленную сумму вклада w(t) как функцию текущего времени. По прошествии временивклад несколько увеличится; его относительный прирост в единицу времени составит:
d = [w(t + Δt) – w(t)]/w(t) Δt.
Мгновенную относительную скорость получим, переходя к пределу при Δt → +:
d = (1/w(t))(dw(t)/dt).
Если рост происходит в соответствии с уравнением (4):
| w(t) = veρ(t – t0), |
то dw(t)/dt = ρveρ(t – t0)
и δ = ρ.
Последний результат разъясняет смысл показателя ρ.
В той ситуации, которая рассматривалась в начале этого раздела, вкладчик имел возможность непрерывно переоформлять вклад из расчета 100 % годовых, т. е. фактически мог получать доход на основе сложных процентов при ρ = 1. Этому значению соответствует рост за год в R = е1 ≈ 2.718 раза, т. е. действительная процентная ставка составляла 171.8 % годовых. Если бы при тех же правилах банк хотел установить действительную процентную ставку 100 %, то при непрерывном начислении дохода следовало бы взять ρ = ln 2 ≈ 0.693.
В примере была использована высокая процентная ставка для того, чтобы было заметнее различие между результатами применения формул простых и сложных процентов.
Разложение показательной функции в степенной ряд:
| eρt = 1 + ρt + (ρt)2/2! + (ρt)3/3! + … |
показывает, что при ρt << 1 можно пренебречь слагаемыми, в которые ρt входит во второй и более высоких степенях:
| eρt » 1+ ρt. |
При этом, во-первых, функции роста для простых и для сложных процентов принимают близкие значения; во-вторых, показатели r и r также близки друг к другу. Например, е0.05 ≈ 1.0512. Если ρ = 5 % в год и t = 1 году, то действительная процентная ставка равна 5.12 % годовых. Если, наоборот, ρ = 5 % годовых, то r = ln 1.05 ≈ 0.0488. Разница, как видим, невелика.
Поэтому в Сбербанке принято следующее правило начисления дохода по вкладам до востребования, допускающим операции не чаще одного раза в день: в пределах календарного года действует правило простых процентов, а в конце года остаток вклада увеличивается на величину образовавшегося за год дохода, что равносильно операции переоформления вклада в нашем примере; при хранении вклада на протяжении ряда лет в целом действует формула (5).
Приведенные здесь соотношения позволяют соизмерять доходы и затраты, относящиеся к различным моментам времени.
Пусть потребитель рассчитывает получить доход W через Т лет. Какому сегодняшнему доходу равноценна для него эта величина? Иными словами, какие ради этого затраты он согласен понести сегодня? Ответ на оба эти вопроса дает величина, получившая название сегодняшней (или текущей) ценности дохода, ожидаемого в будущем.
Получить через Т лет сумму W потребитель мог бы, положив сегодня в банк сумму PV, удовлетворяющую соотношению:
| PV (1+r)T = W. |
Это и есть та сумма, которую потребитель согласен не расходовать на сегодняшнее потребление ради будущего дохода, т. е. сегодняшняя ценность этого дохода.
Итак, сегодняшняя ценность дохода W, ожидаемого через Т лет, равна:
| PV = W/(1+r)T. (6) |
Так, если r = 20 % годовых, Т = 20 лет, то сегодняшняя ценность дохода в 1000 руб. составляет всего:
| PV = 1000/1.220 ≈ 26.08 руб. |
Если же потребитель рассчитывает получать доход в течение ряда лет и его величина, падающая на Т-й год, равна WТ(Т = 1, 2, ..., N), то сегодняшняя ценность распределенного по времени дохода:
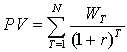 (7) (7)
|
Дата добавления: 2015-12-29; просмотров: 810;
