От порядковой полезности к количественной
Что нужно для количественного измерения
После классических работ Дж. Хикса и Р. Аллена ординалистский подход к полезности завоевал признание экономистов-теоретиков; они утвердились в мнении о том, что поведение потребителя можно достаточно полно описать на основе допущения о наличии у него предпочтений одних наборов благ перед другими.
Какие факты могли бы свидетельствовать о существовании количественной полезности?
Таким фактом, если бы его удалось обнаружить, было бы умение потребителя сопоставлять не только наборы благ, но и различия между парами наборов. Скажем, А > В и С > D. Если потребитель сможет определить, какое из преимуществ — А перед B или С перед D — значительнее, либо же сможет сказать, что оба преимущества равноценны, то эта способность, проявляясь в актах потребительского выбора, могла бы служить основой для построения количественной шкалы измерений.
Действительно, допустим, что А > В и что нам удалось найти такой набор С (А > С > В), что преимущество А перед С равнозначно преимуществу С перед В. Это позволяет утверждать, что полезность набора С расположена “точно в середине” между полезностями A и B, И если мы придали какие-то количественные значения полезности U(А) и U(B), то мы должны полезности набора С приписать значение:
| U(C) = (U(A) + U(B))/2. |
Затем мы можем разделить интервал полезностей между А и С еще раз пополам и продолжить этот процесс сколь угодно далеко, построив шкалу полезностей с любой нужной точностью.
Но мы могли бы построить шкалу не только для полезностей, промежуточных между A и B. Допустим, мы нашли набор D(А > В > D), такой, что превосходство А перед В равнозначно превосходству В перед D. Теперь уже полезность В располагается посредине между А и D, и поэтому:
| U(B) = (U(A) + U(D))/2, |
так что:
| U(D) = 2U(B) – U(A). |
Таким образом, умея сравнивать пары наборов по степени предпочтительности и задав численные значения полезностям двух наборов, мы однозначно определили бы численные значения полезностей любых наборов.
Подобные ситуации возникали и в естественных науках. Примером может служить установление количественной шкалы температур. Человек по своим ощущениям может установить отношения “теплее”, “холоднее” — это не количественное, а лишь порядковое отношение. При контакте двух по-разному нагретых тел одно из них нагревается, другое — охлаждается до выравнивания температуры. “Тепло” (смысл этого понятия до поры до времени был неясен, поэтому мы и берем это слово в кавычки) всегда перетекает от более нагретого тела к более холодному. Но и эти факты не выводят за пределы порядковой шкалы температур.
Положение изменилось, когда появилась концепция, связывающая передачу “тепла” с изменением температуры. Для построения количественной шкалы оказалось достаточно двух принципов: 1) при контакте двух тел общее количество “тепла” в них не изменяется; 2) равные количества “тепла”, переданные одинаковым телам, вызывают одинаковые изменения температуры.
Если мы, смешав воду из сосудовА и В в равных количествах, получили воду точно такой же температуры, что и в сосуде С, у нас есть основания считать, что разность температур между А и С такая же, как между С и В. Если в сосуде А только что растаял лед и мы приняли его температуру за 0, а в сосуде В вода кипела, и мы приняли ее температуру за 100, то мы должны придать значение 50 для температуры воды в сосуде С. Теперь мы можем отградуировать термометр. Значения 0 и 100 мы приняли произвольно. Поступив таким образом, мы построили температурную шкалу Цельсия. Задавая другие значения, мы изменили бы начало отсчета и единицу температуры; при соответствующем выборе мы могли бы получить температурные шкалы Реомюра или Фаренгейта. Переход от одной из них к другой выражается соотношением:
| t1 = a + bt2. |
Свободный член а характеризует перенос начала отсчета, а коэффициент b — соотношение единиц.
Вильфредо Парето, анализируя сложившуюся к последнему десятилетию XIX в. количественную теорию полезности, увидел в ней слабое звено. Поскольку, по мнению Парето, поведение потребителя не обнаруживает его способности сопоставлять одну пару наборов с другой, гипотеза о существовании количественной меры полезности не вытекала из наблюдаемых фактов и ее отрицание не входило в противоречие с опытом.
Значит, она “лишняя”, и нужно строить теорию предпочтения, обходясь без нее. аков был методологический принцип, уже на протяжении веков утвердившийся в науке и получивший название “бритва Оккама”.
Позднее Дж. Хикс и Р. Аллен построили развитую теорию потребления, базирующуюся лишь на порядковых шкалах индивидуальных предпочтений.
Между тем факты потребительского поведения, для описания которых порядковое представление о полезности недостаточно, существовали. Но они относились к таким аспектам потребительского выбора, которые в то время не привлекали внимания экономистов-теоретиков.
Случайные полезности
Homo oeconomicus, совершая тот или иной выбор, не всегда с полной определенностью знает его последствия. Это относится и к потребительскому выбору. Вы приобрели фарфоровую чашку и желаете насладиться ее красотой, но назавтра после покупки случайно поставили ее мимо стола, и покупка оказалась “менее полезной”, чем вы рассчитывали.
Или вы купили арбуз, и он оказался гораздо вкуснее, чем можно было подумать по его виду. Но все могло случиться по-иному: чашка могла бы служить вам много лет и ее ценность повышалась бы, а арбуз мог оказаться невкусным. Полезность покупки могла оказаться той или иной и из-за изменения условий ее использования (классический пример в новелле О’Генри “Дары волхвов”). Помимо этих эпизодов человек сознательно совершает ряд действий, результаты которых носят случайный характер. Он участвует в лотереях и играет в азартные игры. Он страхует свою жизнь и свое имущество, регулярно внося страховую плату и надеясь, что с ним не произойдет “страховой случай”, но не исключая такой возможности. Теория игр, созданная в 20-е гг. одним из самых блестящих ученых XX в. Джоном фон Нейманом, рассматривала поведение “игрока” в условиях, когда последствия его “хода” полностью не определяются его выбором. Более того, оказалось, что игрок, стремящийся к максимальному выигрышу, при определенных условиях должен делать случайные ходы. Теория игр породила новые подходы к анализу поведения экономического субъекта. Основные теоретические результаты в этом направлении были изложены Джоном фон Нейманом и Оскаром Моргенштерном в фундаментальном труде “Теория игр и экономическое поведение”, вышедшем в свет в 1943 г. (в русском переводе в 1970 г.).
Основное допущение, принятое Дж. фон Нейманом и О. Моргенштерном, состоит в том, что потребитель и в случайных ситуациях ведет себя рационально. А это значит, что, производя свой выбор, он сопоставляет не только варианты с однозначными исходами, но и такие варианты, исходы которых имеют случайную полезность. В последнем случае потребитель должен знать как все возможные исходы, так и их вероятности.
Оказалось, что в таком допущении содержится все необходимое для существования количественной меры полезности.
Авторы приводят такой пример. Некто предпочитает стакан чая (Ч) чашке кофе (К), а чашку кофе — стакану молока (М). Допустим, что он поставлен перед выбором: чашка кофе или стакан с неизвестным содержимым, которое с равными вероятностями может оказаться чаем и молоком. Если субъект выбрал кофе, это значит, что из двух предпочтений (Ч > К) и (К > М) второе оказалось более значимым. Следовательно, по своей полезности кофе ближе к чаю, чем к молоку. Если бы он выбрал стакан с неизвестным содержимым, это позволило бы сделать противоположный вывод. Если, наконец, ему безразлично, какую из двух возможностей выбрать, то это означает, что оба предпочтения, Ч > К и К > М, для него равноценны и полезность чашки кофе находится ровно посредине между полезностями стакана чая и стакана молока. Как мы уже видели, возможность сравнивать пары благ или их наборов — это уже основание для построения количественной шкалы полезностей.
Как могут сравниваться между собой численные значения полезностей решений, если каждое из них может иметь различные исходы с разными вероятностями?
Рассмотрим самый простой случай. Допустим, что некоторый выбор влечет за собой два возможных исхода, дающих выигрыш в размере u1 и u2 соответственно. Вероятности исходов могут быть неодинаковыми. Допустим, что выбор был произведен N раз, и при этом N1 раз наступил первый исход, а N2 = N – N1— второй. Тогда общая сумма выигрыша равна N1u1 + N2u2 а для одного акта выбора выигрыш в среднем равен:
| u = (N1u1 + N2u2)/N = au1 + (1 – a)u2, |
где a = N1/N— доля первого исхода, 1 – a = N1/N— доля второго исхода. При большом числе повторений и мало отличаются от вероятностей каждого исхода. Взяв величину равной вероятности первого исхода, мы можем рассматривать величину и как меру случайного выигрыша. Например, если величины выигрыша равнялись 20 и 10 единиц с вероятностями 0.6 и 0.4, то и = 0.6 • 20 + 0.4 • 10= = 16 единицам.
В более общем случае, если m возможных исходов дают выигрыши u1, u2, ..., um с вероятностями (так что ), в качестве числовой меры случайного выигрыша мы могли бы принять:
| u = a1u1 + a2u2 + … +amum. |
Показатель такого вида называется математическим ожиданием и играет важную роль в теории вероятностей. Заметим, что математическое ожидание случайного выигрыша зависит и от выигрышей при различных исходах, и от вероятностей каждого из них. Если, как и раньше, выигрыши равны 20 и 10 единицам, а вероятность а пробегает все значения от 0 до 1, то математическое ожидание принимает все значения от 10 до 20 единиц. И если у нас есть вариант выбора с фиксированным (не случайным) промежуточным выигрышем, скажем, 14 единиц, то можно подобрать такую вероятность a, что случайный выигрыш окажется равноценным рассматриваемому фиксированному (как легко проверить, в данном случае a = 0.4).
Лотерея как средство измерения полезности
Как мы видели, ординалистский подход к полезности вовсе не запрещает ее количественного выражения; он допускает большое разнообразие шкал, требуя от них лишь взаимной монотонности. Именно этот произвол в выборе шкал, при котором требуется лишь, чтобы переход от одной шкалы к другой не нарушал порядка (т. е. чтобы деления на линейках рис. 9 не были перепутаны), и означает, что мы имели дело с порядковой полезностью.
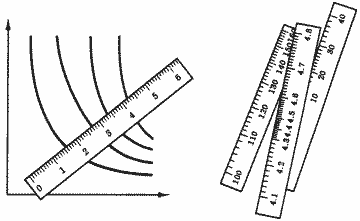
Рис. 9. Ординалистская функция полезности. Кривым безразличия могут быть присвоены числовые значения с помощью любой монотонной шкалы. Все изображенные на рисунке линейки в равной степени пригодны для этой цели.
Допустим ли такой же произвол в случае, когда наш выбор может иметь случайные исходы, а в качестве числовой меры случайного исхода используется показатель типа математического ожидания? Легко убедиться, что нет. Сравним два варианта выбора. Первый приводит к случайному результату с двумя исходами А и В (рис. 10), имеющими равные вероятности 0.5 и 0.5; второй — к промежуточному (по предпочтениям) неслучайному результату С.
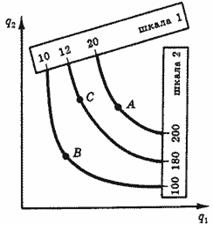
Рис. 10. Случайная полезность в разных шкалах
Допустим, что в некоторой шкале u1(А) = 20, u1(B)= = 10 и u1(С) = 12. Полезность первого варианта выбора определяется величиной 0.5•20 + 0.5•10= =15, и он предпочтительнее второго, полезность которого в этой шкале всего 12 единиц.
Теперь рассмотрим иную шкалу, в которой u1(А) = 200, u2(В) = 100 и u2(С) = 180.
Порядковые отношения, устанавливаемые этой шкалой, совпадают с предыдущей. Но в ней полезность первого выбора равна 0.5•200 + 0.5•100=150 единиц, и в этой шкале он уступает второму.
Мы пришли к противоречивому результату, а это значит, что, имея дело со случайными последствиями решений и используя для их оценки математические ожидания полезностей, мы не можем выбирать для измерения полезностей шкалы, согласованные друг с другом только в отношении порядка. Какая-то из рассмотренных нами шкал, а может быть, и обе, не годятся для представления случайных полезностей. Дж. фон Нейман и О. Моргенштерн разработали систему аксиом количественной полезности. Из этих аксиом следует существование такой функции полезности, математическое ожидание значений которой согласовано с предпочтениями субъекта.
А раз такая функция существует, можно представить себе инструмент для измерения ее значений. Всякое измерение есть сравнение с эталоном. В нашем случае в качестве эталона следовало бы выбрать такую вещь, приобретение которой вело бы к случайным результатам, сильно различающимся по полезности. Идеальным примером подобной вещи служит лотерейный билет: покупатель, изучив условия лотереи, знает, какие в ней разыгрываются призы и может оценить вероятность получения каждого из них.
Единственное, чего он не знает, достанется ли ему выигрыш.
Ситуация, рассмотренная нами выше и иллюстрируемая рис. 10, может рассматриваться как дилемма, стоящая перед потребителем: купить ли ему вполне определенный набор благ С или билет беспроигрышной лотереи, в которой разыгрывается поровну “хороших” наборов А и наборов “похуже” В. Аксиома рациональности в теории Неймана—Моргенштерна утверждает, что потребитель в состоянии решить, какой из покупок — набору С или лотерейному билету — он отдает предпочтение. Рассмотрим теперь лотерею, в которой разыгрываются два приза: соответствующий самому высокому уровню удовлетворения потребностей субъекта Х (“хороший”) и самому низкому П (“плохой”). Произвольно установим значения функции полезности U(П) = 10, U(X) = 20.
Оказывается, мы тем самым однозначно установили значения функции полезности для всех наборов благ. Допустим, что потребитель сравнивает приобретение некоторого конкретного набора благ с участием в такой лотерее. Если вероятность выигрыша Х велика (а вероятность 1 — выигрыша П мала), то он, пожалуй, предпочтет лотерею. Если же величина слишком мала, то он откажется от лотереи в пользу набора С. При некотором промежуточном значении вероятности, обозначим его , оба варианта окажутся равноценными. Если считать, что U(Q) —та самая функция полезности, существование которой следует из принятых аксиом, то должно выполняться равенство:
| U(C) = aCU(X) + (1 – aC)U(П) = 20aC + 10(1 – aC), |
а это значит, что мы однозначно определили полезность набора С. Так, если aC = 0.6, то U(C) = 16, как в одном из рассмотренных выше примеров. Мы выбрали призы Х и П таким образом, что любой набор благ окажется промежуточным (в смысле порядка). Поэтому для любого набора благ можно подобрать соответствующее значение вероятности , при котором лотерея с точки зрения субъекта не лучше и не хуже этого набора, и описанная нами процедура однозначно определила бы числовое значение полезности любого набора.
Напомним, что значения U(X) и U(П) мы назначили произвольно. Но, закрепив их, мы уже однозначно задали всю шкалу полезностей. Придавая произвольное значение U(П) = a и любое, но обязательно большее, значение U(X) = а + b, мы для набора С получили бы значение полезности:
| U(C) = aC(a + b) + (1 – aC)a = a + baC. |
Таким образом, все шкалы различаются между собой только значением свободного члена а (это может быть любое число) и коэффициента пропорциональности b (это может быть любое положительное число). Иными словами, любая шкала полезности по Нейману—Моргенштерну может быть получена из любой другой с помощью линейного преобразования — изменения начала отсчета и масштаба. Наиболее естественной представляется шкала, в которой U(П) = 0, U(X) = 1. Здесь полезность любого набора совпадает с вероятностью выигрыша “хорошего” приза в “безразличной” лотерее, U(C) = aC.
Теория полезности Неймана-Моргенштерна возникла тогда, когда в экономической науке уже утвердилось представление о том, что порядковая полезность достаточно полно описывает поведение потребителя. Новый взгляд, требовавший возврата (хотя и на ином уровне) к количественной полезности, естественно, вызвал активную дискуссию в ученом мире. К настоящему времени сферы применения обоих подходов в основном разделились.
Там, где имеется однозначная связь между выбором и его последствиями, вполне достаточен ординалистский подход, и в наших дальнейших лекциях мы ограничимся порядковой полезностью. Но в тех задачах, где нужно учесть случайный характер этой связи, требуется количественное измерение полезности.
Дата добавления: 2015-12-29; просмотров: 721;
