Классификация криптографических систем

Существует несколько классификаций криптографических систем (шифров). Рассмотрим некоторые из них.

I. По области применения различают криптосистемы ограниченного и общего использования.

Стойкость криптосистемы ограниченного использования основывается на сохранении в секрете алгоритма криптографического преобразования в силу его уязвимости, малого количества ключей или отсутствия таковых (секретные кодовые системы).

Стойкость криптосистемы общего использования основывается на секретности ключа и сложности его подбора потенциальным противником.

II. По особенностям алгоритма шифрования криптосистемы общего использования можно разделить на следующие виды.

В одноключевых системах для шифрования и дешифрования используется один и тот же ключ.

В шифрах перестановки все буквы открытого текста остаются в зашифрованном сообщении, но меняют свои позиции. В шифрах замены наоборот, позиции букв в шифровке остаются теми же, что и у открытого текста, но символы открытого текста заменяются символами другого алфавита.

В аддитивных шифрах буквы алфавита заменяются числами, к которым затем добавляются числа секретной случайной (псевдослучайной) числовой последовательности (гаммы). Состав гаммы меняется в зависимости от используемого ключа. Обычно для шифрования используется логическая операция «Исключающее ИЛИ» (XOR). При дешифровании та же гамма накладывается на зашифрованные данные. Гаммирование широко используется в военных криптографических системах.

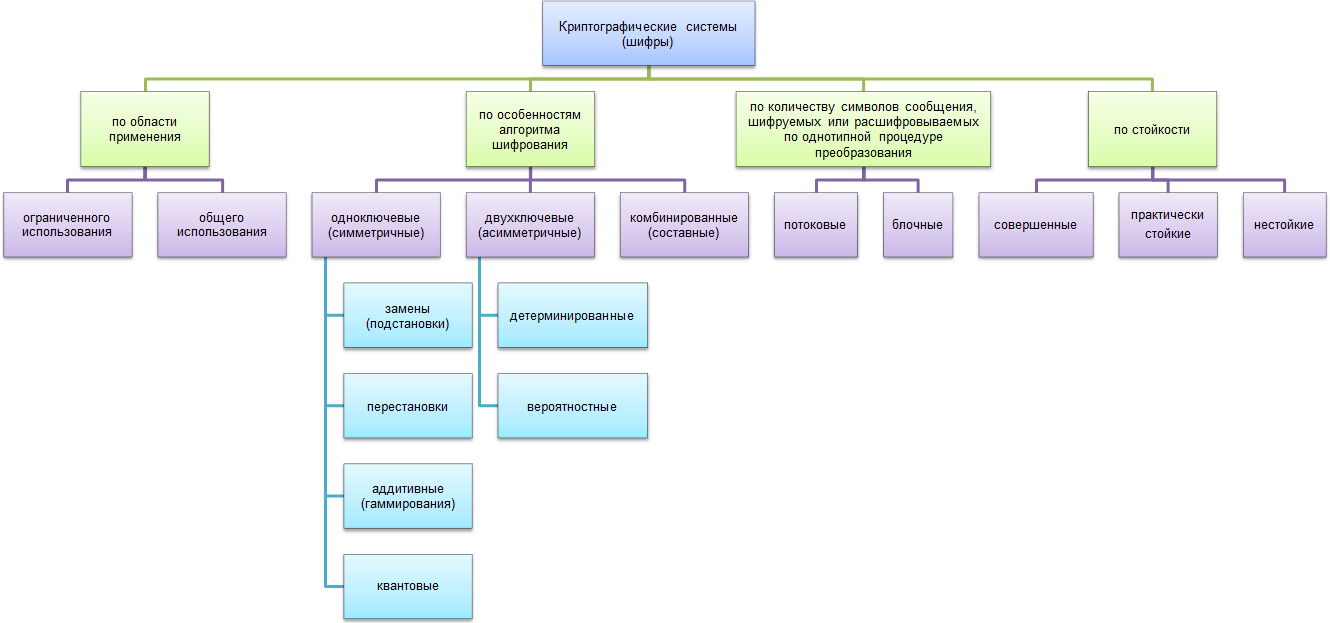
Рис. Классификация криптографических алгоритмов

Квантовая криптография вносит в процесс шифрования естественную неопределенность квантового мира. Процесс отправки и приёма информации выполняется посредством объектов квантовой механики (например, при помощи электронов в электрическом токе, или фотонов в линиях волоконно-оптической связи). Самым ценным свойством этого вида шифрования является то, что при посылке сообщения отправляющая и принимающая сторона с достаточно большой вероятностью могут установить факт перехвата зашифрованного сообщения.

В двухключевых системах для шифрования и дешифрования используется два совершено разных ключа. При использовании детерминированного алгоритма шифрование и расшифрование посредством соответствующей пары ключей возможно только единственным способом. Вероятностный алгоритм при шифровании одного и того же исходного сообщения с одним и тем же ключом может давать разные шифртексты, которые при расшифровке дают один и тот же результат.

Комбинированные (составные) методы предполагают использование для шифрования сообщения сразу нескольких методов (например, сначала замена символов, а затем их перестановка).

Все шифры по алгоритму преобразования также делят на потоковые и блочные. В потоковых шифрах преобразование выполняется отдельно над каждым символом исходного сообщения. Для блочных шифров информация разбивается на блоки фиксированной длины, каждый из которых шифруется и расшифровывается отдельно.

III. По количеству символов сообщения (или его кодовой замены), шифруемых или расшифровываемых по однотипной процедуре преобразования:

- потоковые – процедура преобразование применяется к отдельному символу сообщения;

- блочные – процедура преобразование применяется к набору (блоку) символов сообщения;

Отличить потоковый шифр от блочного можно по следующему признаку - если в результате разбиения исходного сообщения на отдельные символы и применения к ним однотипной процедуры преобразования получаемая шифрограмма эквивалентна той, которая получается при применении преобразования ко всему исходному сообщению, то шифр потоковый, иначе блочный.

По стойкости шифры делятся на три группы:

- совершенные (абсолютно стойкие, теоретически стойкие) – шифры, заведомо неподдающиеся вскрытию (при правильном использовании). Дешифрование секретного сообщения приводит к нескольким осмысленным равновероятным открытым сообщениям;

- практически (вычислительно, достаточно) стойкие – шифры, вскрытие которых за приемлемое время невозможно на современном или перспективном уровне вычислительной техники. Практическая стойкость таких систем базируется на теории сложности и оценивается исключительно на какой-то определенный момент времени с двух позиций:

- вычислительная сложность полного перебора;

- известные на данный момент слабости (уязвимости) и их влияние на вычислительную сложность;

- нестойкие шифры.