Код Хэмминга - это групповой код.

Это следует из того, что 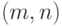-код Хэмминга можно получить матричным кодированием, при помощи -матрицы, в которой столбцы с номерами не степенями 2 образуют единичную подматрицу. Остальные столбцы соответствуют уравнениям шага 4 построения кода Хэмминга, т.е. 1-му столбцу соответствует уравнение для вычисления 1-го контрольного разряда, 2-му - для 2-го, 4-му - для 4-го и т.д. Такая матрица будет при кодировании копировать биты сообщения в позиции не степени 2 кода и заполнять другие позиции кода согласно схеме кодирования Хэмминга.

Пример. Кодирующая матрица для 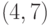-кода Хэмминга –

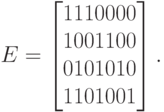
Ее столбцы с номерами 3, 5, 6 и 7 образуют единичную подматрицу. Столбцы с номерами 1, 2 и 4 соответствуют уравнениям для вычисления контрольных бит, например, уравнению соответствует столбец 1101, т.е. для вычисления первого контрольного разряда берутся 1, 2 и 4 биты исходного сообщения или биты 3, 5 и 7 кода.

К 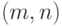-коду Хэмминга можно добавить проверку четности. Получится 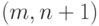-код с наименьшим весом ненулевого кодового слова 4, способный исправлять одну и обнаруживать две ошибки.

Коды Хэмминга накладывают ограничения на длину слов сообщения: эта длина может быть только числами вида 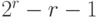: 1, 4, 11, 26, 57, Но в реальных системах информация передается байтам или машинными словами, т.е. порциями по 8, 16, 32 или 64 бита, что делает использование совершенных кодов не всегда подходящим. Поэтому в таких случаях часто используются квазисовершенные коды.

Квазисовершенные 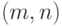-коды, исправляющие одну ошибку, строятся следующим образом. Выбирается минимальное 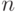так, чтобы

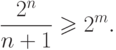
Каждое кодовое слово такого кода будет содержать 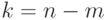контрольных разрядов. Из предыдущих соотношений следует, что

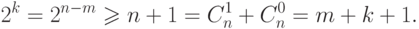
Каждому из 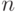разрядов присваивается слева-направо номер от 1 до 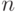. Для заданного слова сообщения составляются 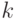контрольных сумм по модулю 2 значений специально выбранных разрядов кодового слова, которые помещаются в позиции-степени 2 в нем: для 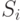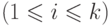выбираются разряды, содержащие биты исходного сообщения, двоичные числа-номера которых имеют в 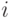-м разряде единицу. Для суммы 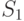это будут, например, разряды 3, 5, 7 и т.д., для суммы 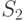- 3, 6, 7 и т.д. Таким образом, для слова сообщения 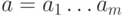будет построено кодовое слово . Обозначим 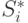сумму по модулю 2 разрядов полученного слова, соответствующих контрольной сумме 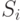и самой этой контрольной суммы. Если 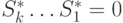, то считается, что передача прошла без ошибок. В случае одинарной ошибки будет равно двоичному числу-номеру сбойного бита. В случае ошибки, кратности большей 1, когда , ее можно обнаружить. Подобная схема декодирования не позволяет исправлять некоторые двойные ошибки, чего можно было бы достичь, используя схему декодирования с лидерами, но последняя значительно сложнее в реализации и дает незначительное улучшение качества кода.

Пример построения кодового слова квазисовершенного 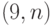-кода, исправляющего все однократные ошибки, для сообщения 100011010.

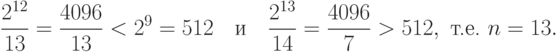
Искомое кодовое слово имеет вид 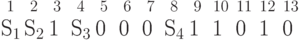. Далее нужно вычислить контрольные суммы.

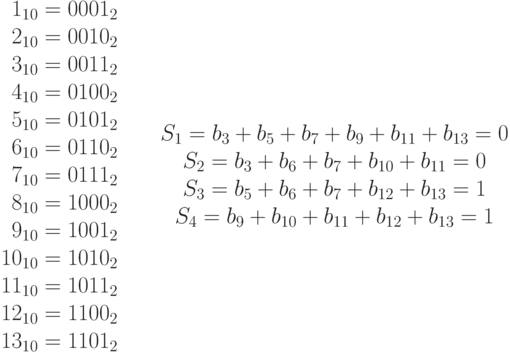
Таким образом, искомый код - 0011000111010. Если в процессе передачи этого кода будет испорчен его пятый бит, то приемник получит код 0011100111010. Для его декодирования опять вычисляются контрольные суммы:

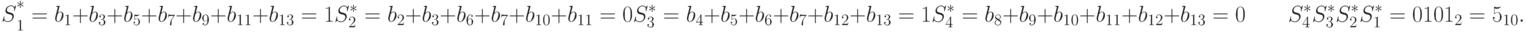
Приемник преобразует изменением пятого бита полученное сообщение в отправленное передатчиком, из которого затем отбрасыванием контрольных разрядов восстанавливает исходное сообщение.

Совершенный код Хэмминга также можно строить по рассмотренной схеме, т.к. для него .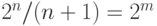

Для исправление одинарной ошибки к 8-разрядному коду достаточно приписать 4 разряда ( 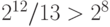), к 16-разрядному - 5, к 32-разрядному - 6, к 64-разрядному - 7.

Упражнение 41 Может ли 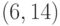-код, минимальное расстояние между кодовыми словами которого 5, быть совершенным?

Упражнение 42 Построить кодовые слова квазисовершенного 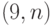-кода, исправляющего однократные ошибки, для тех сообщений, которые соответствуют числам 55, 200 и декодировать слова 1000001000001, 1100010111100, полученные по каналу связи, использующему этот код.