Технология разработки экспертных систем

Технология их разработки ЭС, включает в себя шесть этапов (рис.5): этапы идентификации, концептуализации, формализации, выполнения, тестирования, опытной эксплуатации. Рассмотрим более подробно последовательности действий, которые необходимо выполнить на каждом из этапов.

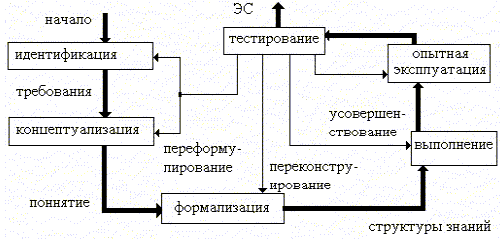
1) На этапе идентификации необходимо выполнить следующие действия:

определить задачи, подлежащие решению и цели разработки,

определить экспертов и тип пользователей.

2) На этапе концептуализации:

проводится содержательный анализ предметной области,

выделяются основные понятия и их взаимосвязи,

определяются методы решения задач.

3) На этапе формализации:

выбираются программные средства разработки ЭС,

определяются способы представления всех видов знаний,

формализуются основные понятия.

4) На этапе выполнения (наиболее важном и трудоемком) осуществляется наполнение экспертом БЗ, при котором процесс приобретения знаний разделяют:

на «извлечение» знаний из эксперта,

на организацию знаний, обеспечивающую эффективную работу ЭС,

на представление знаний в виде, понятном для ЭС.

Процесс приобретения знаний осуществляется инженером по знаниям на основе деятельности эксперта.

5) На этапе тестирования эксперт и инженер по знаниям с использованием диалоговых и объяснительных средств проверяют компетентность ЭС. Процесс тестирования продолжается до тех пор, пока эксперт не решит, что система достигла требуемого уровня компетентности.

6) На этапе опытной эксплуатации проверяется пригодность ЭС для конечных пользователей. По результатам этого этапа возможна существенная модернизация ЭС.

Процесс создания ЭС не сводится к строгой последовательности этих этапов, так как в ходе разработки приходится неоднократно возвращаться на более ранние этапы и пересматривать принятые там решения.

Количество информации в случае различных вероятностей событий определяется по формуле Шеннона:

Существует множество ситуаций, когда возможные события имеют различные вероятности реализации. Рассмотрим примеры таких событий.

1. При случайном падении бутерброда вероятность падения его маслом вниз (более тяжёлой стороной) больше, чем маслом вверх.

2. В коробке 20 карандашей, из них 15 красных и 5 чёрных. Вероятность вытащить наугад красный карандаш больше, чем чёрный.

Количество информации в сообщении о некотором событии зависит от его вероятности. Чем меньше вероятность события, тем больше информации оно несёт.
P = K/N, где К – количество случаев реализации одного из исходов события, N – общее число возможных исходов одного из событий 2ⁱ = log₂(1/p), где i – количество информации, p – вероятность события

Задача 1.В коробке 50 шаров, из них 40 белых и 10 чёрных. Определить количество информации в сообщении о вытаскивании наугад белого шара и чёрного шара.

Решение: Вероятность вытаскивания белого шара - P1 = 40/50 = 0,8

Вероятность вытаскивания чёрного шара P₂ = 10/50 = 0,2

Количество информации о вытаскивании белого шара i₁ = log2(1/0,8) = log21,25

= log1,25/log2 » 0,32 бит

Количество информации о вытаскивании чёрного шара i₂ = log2(1/0,2) = log25 = log5/log2 » 2,32 бит

Ответ: 0,32 бит; 2,32 бит

Задача 2.В озере живут караси и окуни. Подсчитано, что карасей 1500, а окуней - 500. Сколько информации содержится в сообщениях о том, что рыбак поймал карася, окуня, поймал рыбу?

Решение:События поимки карася или окуня не являются равновероятными, так как окуней в озере меньше, чем карасей.

Общее количество карасей и окуней в пруду 1500 + 500 = 2000.

Вероятность попадания на удочку карася

p₁ = 1500/2000 = 0,75, окуня p₂ – 500/2000 = 0,25.

I₁ = log₂(1/p1), I₁ = log2(1/p2), где I₁ и I₂ – вероятности поймать карася и окуня соответственно.

I₁ = log₂(1 / 0,75) » 0,43 бит, I₂ = log₂(1 / 0,25) » 2 бит – количество информации в сообщении поймать карася и поймать окуня соответственно.

Количество информации в сообщении поймать рыбу (карася или окуня) рассчитывается по формуле Шеннона

I = - p₁log₂p₁ - p₂log₂p₂

I = - 0,75*log₂0,75 - 0,25*log₂0,25 = - 0,75*(log0,75/log2)-0,25*(log0,25/log2) = 0,604 бит » 0.6 бит.

Ответ: в сообщении содержится 0,6 бит информации

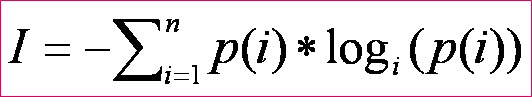где Pi – вероятность i-го события, N – количество возможных событий     Формула была предложена в 1948 г.

Клод Шеннон американский учёный, (30 апреля 1916 - 24 февраля 2001)