Маршруты, цепи, циклы

Маршрутом в графе 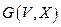называется конечная последовательность ребер вида: 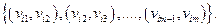Этот маршрут обозначают: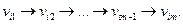

Петля называется тривиальным маршрутом.

Длиной маршрута называется число ребер в нем.

Маршрут называется цепью, если все его ребра различны.

Маршрут называется простой цепью, если все его вершины различны, за исключением, быть может, первой и последней.

Если 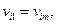то цепь называется замкнутой.

Замкнутая простая цепь, содержащая хотя бы одно ребро, называется циклом.

Две вершины 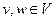называются эквивалентными или связанными, если существует простая цепь из одной вершины в другую.

Второе определение связного графа. Граф называется связным, если любые две его вершины являются связанными.

Теорема. Первое и второе определения связности равносильны.

Связанность вершин является отношением эквивалентности на множестве вершин графа.

Свойства отношения эквивалентности:

1) рефлексивность ;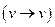

2) симметричность (если 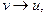то );

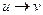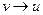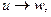3) транзитивность (если и то )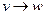

Отношение эквивалентности задает разбиение графа на компоненты связности.

Теорема. Каждый граф единственным образом представляется в виде объединения непересекающихся связных подграфов (компонент связности).

Число реберв графе минимально, если удаление любого ребра приводит к увеличению компонент связности.

Если при удалении какого-то ребра в графе, число компонент связности увеличилось на единицу, то это ребро называется мостом или перешейком.