Корневой метод оценки качества управления
Это косвенный метод, основанный на определении границ области расположения корней характеристического уравнения на комплексной плоскости, что дает возможность приблизительно оценить качество управления.
Пусть имеется дифференциальное уравнение замкнутой САУ:
(a0pn + a1pn-1 + a2pn-2 + ... + (an)y = (b0pm + b1pm-1 + ... + bm)u.
Передаточная функция САУ
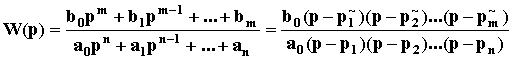 ,
,
где p~1,p~2,...,p~m - нули передаточной функции, p1,p2,...,pn - полюса передаточной функции.
 Переходный процесс зависит как от полюсов, так и от нулей, то есть определяется как левой, так и правой частями дифференциального уравнения. Это существенно усложняет анализ. Поэтому рассмотрим частный, но весьма распространенный случай, когда передаточная функция замкнутой САУ не имеет нулей:
Переходный процесс зависит как от полюсов, так и от нулей, то есть определяется как левой, так и правой частями дифференциального уравнения. Это существенно усложняет анализ. Поэтому рассмотрим частный, но весьма распространенный случай, когда передаточная функция замкнутой САУ не имеет нулей:
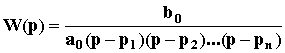 .
.
Тогда уравнение динамики приобретает вид:
(a0pn + a1pn-1 + a2pn-2 + ... + an)y = b0u.
Общее решение данного уравнения имеет вид:
y(t) = yсв + yвын = åAiepit + bо/an.
Время переходного процесса tпп определяется длительностью свободного процесса, который представляет собой сумму n экспоненциально затухающих составляющих (рис.88). Затухание каждой из составляющих определяется вещественной частью соответствующего плюса pi, которая для устойчивых систем должна быть отрицательна. Длительность переходного процесса определяется в основном свободной составляющей, имеющей наименьшее затухание, то есть наименьшее абсолютное значение вещественной части соответствующего полюса.
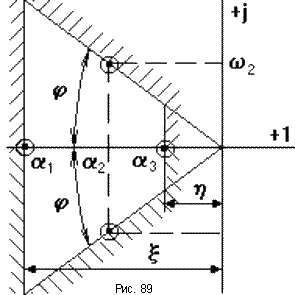
Если изобразить все полюса в комплексной плоскости корней (рис.89), то данный полюс (или пара комплексно сопряженных полюсов) будет наиболее близко расположен к мнимой оси.
Для приблизительной оценки качества САУ на плоскости корней выделяется область в виде трапеции, на сторонах которой находится хотя бы по одному корню, все остальные корни - внутри данной области. Эта область характеризуется параметрами: h - степень устойчивости (равна расстоянию от мнимой оси до ближайшего корня или пары комплексно сопряженных корней);m = tg(j) - колебательность (характеризует колебательность переходного процесса и величину перерегулирования);x - своего названия не имеет, равна вещественной части наиболее удаленного от мнимой оси корня.
По степени устойчивости h можно приблизительно вычислить время переходного процесса, которое определяется по моменту, когда свободная составляющая с наименьшим затуханием уменьшится до величины 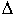
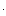 Ai, где Ai - начальное значение данной составляющей, то на рис.84:
Ai, где Ai - начальное значение данной составляющей, то на рис.84:
yсв3(t) = A3 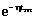 =
= 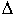
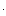 A3 = >
A3 = > 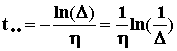 .
.
В общем случае, когда передаточная функция замкнутой САУ имеет нули, то использование данного метода может дать большую ошибку. Однако всегда качество управления будет тем лучше, чем больше h и меньше m, поэтому данный метод имеет смысл для любых САУ, но приближенно.
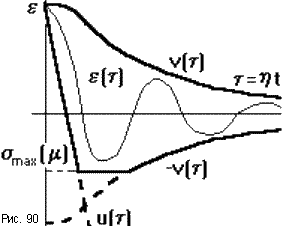
Зная значения h, x, m можно оценить область, за которую кривая переходного процесса выходить не будет (рис.90). Для этого строятся две кривые: u(t,h) - миноранта и v(t,h) - мажоранта, ограничивающая кривую переходного процесса соответственно снизу и сверху так, что u(t,h)  e(t)
e(t)  v(t,h), где e(t) = yo-y(t). Формулы для определения миноранты и мажоранты берутся в справочниках для конкретных случаев.
v(t,h), где e(t) = yo-y(t). Формулы для определения миноранты и мажоранты берутся в справочниках для конкретных случаев.
Дата добавления: 2015-12-26; просмотров: 653;
