Метод годичного параллакса.

Если наблюдать звезду А из двух разных точек земной орбиты З₁ и З₂ с интервалом полгода, то ее положения на фоне более далеких звезд А₁ и А₂ окажутся смещенными на угол 2р. Угол р называется годичным параллаксом.

Измерив р и зная 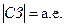, можно найти расстояние до звезды:

.

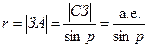Угол р очень мал даже для ближайших звезд, поэтому 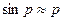(рад), причем радианы удобно выразить в угловых секундах: 1 рад = .

,

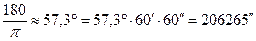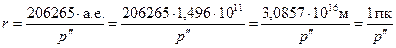где 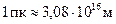– параллакс-секунда (парсек) – единица расстояний до звезд и галактик.

Окончательно, 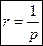, где ; .

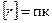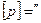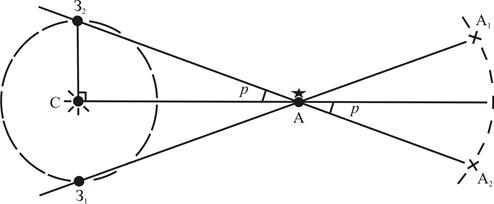
Рисунок 16

Пример. Расстояние до Веги (α Лиры).

Параллакс Веги 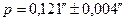; расстояние до этой звезды 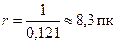; погрешность 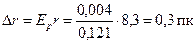; окончательно, .

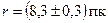Очевидно, что возможности метода ограничены.

,

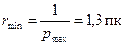где 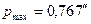– параллакс ближайшей звезды (Проксима Центавра);

,

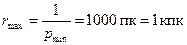где 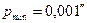– наименьшая погрешность измерения углов.

Итак, границы применимости метода годичного параллакса: .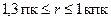

Гершель ввел единицу расстояний световой год (св. год). 1 св. год – это расстояние, проходимое светом за 1 год.

Считая, что в вакууме скорость света примерно равна 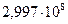м/с, в году 365 суток, в сутках 24 часа, а в сутках 3600 секунд, световой год можно выразить в метрах:

1 cв. год = 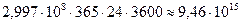м.

1 пк ≈ 3,26 св.года.

Расстояние до ближайшей звезды, Проксимы из созвездия Центавра, составляет примерно 1,3 пк ≈ 4,25 св. года, т.е. свет этой звезды идет до Земли в течение 4,25 лет.