Помехоустойчивое кодирование

Ясно, что цифровой сигнал, как и аналоговый, критичен к влиянию помех. Вероятность появления ошибок в канале связи зависит от самого канала. В кабельных системах передач, к примеру, она будет на много меньше, чем в системах цифровой радиосвязи, но все равно она будет не нулевой. Без возможности исправления ошибок качество принимаемого сигнала будет неудовлетворительным. При вероятности появления ошибок 10^-4 и скорости цифровых данных 100 Мбит/с каждую секунду будут появляться тысячи ошибок, а если принять во внимание, что значение отсчета при ошибке может меняться многократно, можно представить, какое качество изображения будет на приемном конце.

За счет чего возможно исправление ошибок? Для примера возьмем наш родной русский язык. Представим, что слова русского языка – кодовые слова, а буквы, из которых складываются слова – биты информации. А теперь представим, что мы читаем текст, в котором есть грамматические ошибки или слушаем человека с дефектом речи. Мы понимаем, что написано и что говорит человек, хотя, как приемник зрительной и звуковой информации, принимаем ошибочные символы. Это возможно за счет избыточности языка, т.е. похожие слова отличаются друг от друга более, чем на одну букву и при изменении любой из букв получается слово, которого нет в русском языке и это слово очень похоже на исходное. Конечно, существуют слова, при изменении одной буквы в которых образуется другое слово, но их немного, и мы все равно определим ошибку по смыслу фразы.

Такой же метод используется и в цифровых системах передач – передаваемые по каналу связи кодовые слова отличаются друг от друга более чем на один разряд, т.е. не все возможные кодовые слова входят в алфавит кода. Алфавит кода - это совокупность кодовых слов, используемых кодером. При появлении одиночной ошибки возникает слово, не входящее в алфавит кода, что является сигналом об ошибке для декодера, т.к. это слово не могло быть передано.

Принцип помехоустойчивого кодирования можно пояснить с помощью трехмерной модели трехразрядного кода.

На рисунке 14.1а все возможные кодовые слова входят в алфавит кода, шаг Хемминга равен d=1. Шаг Хемминга равен количеству символов, которыми отличаются соседние кодовые слова (они соединены ребрами куба). При ошибке в кодовом слове возникает другое слово, входящее в алфавит кода (невозможны ни определение, ни исправление ошибки).

При шаге Хемминга d=2 (рис 14.1б) при возникновении одиночной ошибки появляется кодовое слово, не входящее в алфавит кода (возможно определение ошибки), но появившееся кодовое слово лежит на одинаковом расстоянии от трех разрешенных, поэтому исправление ошибки невозможно. Примером помехоустойчивого кода с d=2 является код с проверкой на четность, в котором к информационному слову добавляется один проверочный бит, значение которого доводит количество единиц в кодовом слове до четного числа. Он относится к паритетным кодам и способен обнаружить нечетное количество ошибок. Если же количество ошибок будет четным (см. рис.14.1б), то возникнет слово, входящее в алфавит кода, при этом невозможно обнаружение ошибок. Надо заметить, что обнаружение ошибки важно даже в телевизионных цифровых системах передач: к пораженному отсчету можно применить методы пространственной или временной интерполяции (замаскировать ошибку). Пространственная интерполяция – придание пораженному отсчету среднего арифметического соседних, непораженных элементов изображения. Временная интерполяция – придание пораженному отсчету среднего арифметического от тех же самых отсчетов из предыдущего и последующего кадров.

Рис.14.1 Трехмерная модель трехразрядного кода

При d=3 только два кодовых слова из восьми возможных входят в алфавит кода. При возникновении одиночной ошибки получится слово, не входящее в алфавит кода (возможно обнаружение ошибки), при чем это слово будет находиться ближе к исходному, чем и объясняется возможность исправления ошибки. Но при появлении двойной ошибки получившееся слово будет находиться ближе к другому разрешенному. Декодер исправит эту ошибку неправильно. Этим объясняется то, что цифровые системы передач – пороговые: пока количество ошибок не превысило то, на которое рассчитан код, канальный декодер справляется с ними и исправляет правильно; при превышении количеством ошибок разрешенного числа происходит неправильное их исправление, что приводит к невозможности приема цифрового сигнала.

Как видно из рисунка 14.1, помехоустойчивое кодирование возможно за счет введения в цифровой сигнал избыточности (дополнительных символов). Четыре комбинации (рис. 14.1б) можно передать двумя битами, а две (рис. 14.1в) – одним, но при этом не было бы возможным исправление ошибок. Помехоустойчивые коды характеризуются числами k и n, где n – количество символов в информационном слове, приходящем на помехоустойчивый кодер, а k – количество символов в кодовом слове, выходящем с помехоустойчивого кодера. Отношение k/n показывает, во сколько раз скорость цифрового потока на выходе помехоустойчивого кодера больше, чем на его входе, это отношение называют скоростью помехоустойчивого кода. Разность (k-n) равна количеству дополнительных (проверочных) символов в кодовом слове. Чем больше проверочных символов в кодовом слове (избыточность кода), тем больше исправляющая возможность (мощность) помехоустойчивого кода, но при этом растет скорость цифрового потока, передаваемого по каналу связи. Именно поэтому в различных системах передач (спутниковых, кабельных или наземного цифрового вещания) используются отличные друг от друга цифровые системы вещания, в которых определяется компромисс между исправляющей возможностью и скоростью помехоустойчивого кода (DVB-T (наземная), DVB-C (кабельная), DVB-S (спутниковая)).

Помехоустойчивые коды классифицируются:

1. блоковые и сверточные;

2. систематические и несистематические.

В блоковых кодах формирование проверочных символов ведется на основе одного блока информации, например, информационного слова. Декодирование производится на основе одного кодового слова.

В сверточных кодах формирование проверочных символов производится на основе нескольких блоков информации (информационных слов), а декодирование - на основе нескольких кодовых слов. Количество информационных слов, участвующих в формировании проверочных символов в сверточном кодировании определяет длину кодового ограничителя. Принцип работы сверточных кодов можно сопоставить с исправлением ошибок по смыслу (см. пример с русским языком). Сверточные коды еще называют решетчатыми (трилистными).

Систематические коды определяют наличие в кодовом слове информационного в явном виде.

В несистематических кодах информационного слова в кодовом нет, т.е. при помехоустойчивом кодировании информационному слову с количеством символов n ставится в соответствие кодовое слово с количеством символов k.

Пример блокового кода – код Рида-Соломона, наиболее часто используемый в современных цифровых системах. Операции по определению кодового слова на передающем конце и по определению и исправлению ошибок на приемном конце выполняются как действия с многочленами. Если кодируемая информация i описывается набором из n символов (информационное слово), то этому слову можно сопоставить многочлен (14.1):

i(x)=i_n-1x^n-1+i_n-2x^n-2+......+i₁x¹+i₀ (14.1)

где х – основание системы исчисления (для двоичных кодов х=2)

i – значение соответствующего бита информационного слова (0 или 1)

Например, информационное слово 11010011, которое равно 211 уровню, можно записать в виде многочлена:

1*2⁷+1*2⁶+0*2⁵+1*2⁴+0*2³+0*2²+1*2¹+1*2⁰=211

Кодовое слово из k символов, которое будет сопоставлено информационному, также можно представить в виде кодового многочлена (14.2):

c(x)=c_k-1x^k-1+c_k-2x^k-2+......+c₁x¹+c₀ (14.2)

где с – значение соответствующего бита кодового слова

Принцип работы помехоустойчивого декодера заключается в том, что многочлены, соответствующие принятым кодовым словам, должны делится на порождающий без остатка. Если при делении появился остаток, то это значит, что произошла ошибка. Если количество ошибок не превысило расчетную величину, многочлен остатка (синдром) зависит только от конфигурации ошибок, которые вычисляются по синдрому, а затем вычитаются из принятого слова. При этом формируется передаваемое кодовое слово, которое делится на порождающий многочлен, формируя исходное информационное слово.

Для возможности исправления в кодовом слове t ошибок количество проверочных символов в кодовом слове должно быть равно 2t (k-n=2t), степень порождающего многочлена также равна количеству проверочных символов. Порождающий многочлен определяется по формуле (14.3):

g(x)=g_k-nx^k-n+g_k-n-1x^k-n-1+……+g₁x¹+g₀ (14.3)

где g – значение соответствующего бита порождающего слова.

Код Рида-Соломона способен также исправить количество ошибок, равное количеству проверочных символов, при условии, что известно их местоположение (исправление стираний).

В канале связи кроме одиночных ошибок, вызванных шумами, часто встречаются пакетные ошибки, вызванные импульсными помехами, замираниями или выпадениями (при цифровой видеозаписи). При этом пораженными оказываются сотни, а то и тысячи бит информации подряд. Ясно, что ни один помехоустойчивый код не сможет справиться с такой ошибкой. Для возможности борьбы с такими ошибками используются коды-произведения. Принцип действия такого кода изображён на рисунке 14.2.

Рис. 14.2 Коды-произведения. Схема структурная

Передаваемая информация кодируется дважды: во внешнем и внутреннем кодерах. Между ними устанавливается буфер, работа которого показана на рисунке 14.3. Информационные слова проходят через первый помехоустойчивый кодер, называемый внешним, т.к. он и соответствующий ему декодер находятся по краям системы помехоустойчивого кодирования (см. рис. 14.2). Здесь к ним добавляются проверочные символы (формируются кодовые слова). Они, в свою очередь, заносятся в буфер (рис. 14.3а) по столбцам, а выводятся построчно. Этот процесс называется перемешиванием или перемежением.

При выводе строк из буфера к ним добавляются проверочные символы внутреннего кода. В таком порядке информация передается по каналу связи или записывается на магнитную ленту. Условимся, что и внутренний, и внешний коды – коды Рида-Соломона, с двумя проверочными символами, т.е. и тот, и другой могут исправить по одной ошибке в кодовом слове. На приемном конце расположен точно такой же массив памяти (буфер), в который информация заносится построчно, а выводится по столбцам. При возникновении пакетной ошибки (рис. 14.3б крестики в третьей и четвертой строках), она малыми порциями распределяется в кодовых словах внешнего кода и может быть исправлена.

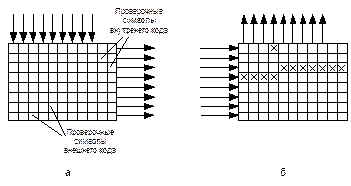
Рис. 14.3 Работа буфера на передающей части (а), принцип исправления пакетных ошибок в декодере (б)

Назначение внешнего кода понятно – исправление пакетных ошибок. Зачем же нужен внутренний код? На рисунке 14.3б, кроме пакетной, показана одиночная ошибка (четвертый столбец, верхняя строка). В кодовом слове, расположенном в четвертом столбце - две ошибки, и они не могут быть исправлены, т.к. внешний код рассчитан на исправление одной ошибки. Для выхода из этой ситуации как раз и нужен внутренний код, который исправит эту одиночную ошибку. Принимаемые данные (рис. 14.2) сначала проходят внутренний декодер, где исправляются одиночные ошибки, затем записываются в буфер построчно, выводятся по столбцам и подаются на внешний декодер, где происходит исправление пакетной ошибки.

Использование кодов-произведений многократно увеличивает мощность помехоустойчивого кода при добавлении незначительной избыточности.