Обшивка со стрингерным подкреплением
Проверка прочности обшивки производится при совместном действии напряжений σ и τ.
При расчете на эксплуатационную нагрузку Рэредукционные коэффициенты φi = Еi/Еφ.
При расчете на Ррисходные коэффициенты φi = σразр/σразр.ф, где индексом "ф" обозначается фиктивный элемент. Это обычно основной элемент панели (пояс, стрингер), который рассматривается как идеально упругий.
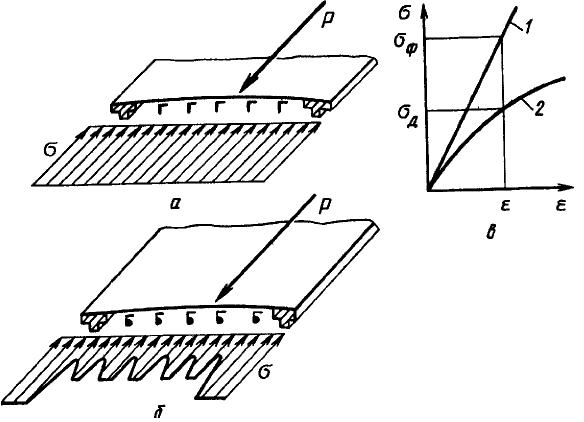 Рис. 14.10, в иллюстрирует разницу между действительным σд и фиктивным σф напряжениями растяну-того элемента при определенном значении удлинения ε.
Рис. 14.10, в иллюстрирует разницу между действительным σд и фиктивным σф напряжениями растяну-того элемента при определенном значении удлинения ε.
Рис 14.10. Напряжения σ в элементах сжатой панели до (а) и после (б) потери устойчивости, действительная (2) и фиктивная (1) диаграммы растяжения (в)
Для сжатых элементов
σразр=σк, (14.2)
а для растянутых
σразр=σв. (14.3)
Здесь σк– нормальные критические напряжения. При достижении этих напряжений происходит потеря устойчивости элемента конструкции.
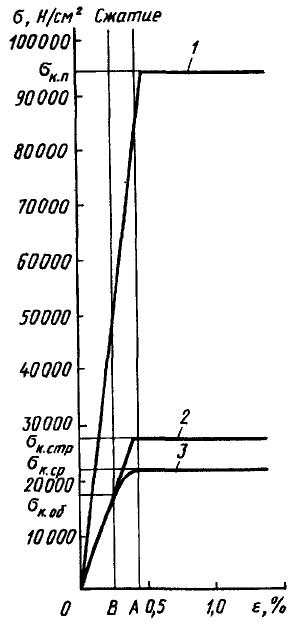
Для расчета модели можно использовать также диаграммы σ-ε (рис. 14.11).
 Расчет прочности растянутой обшивкиведется на действие Ррпо условию
Расчет прочности растянутой обшивкиведется на действие Ррпо условию
σрприв ≤ σразр, (14.4)
где σ = K·σв;
σприв =√σ2обш+4τ2;
K = 0,9 — коэффициент ослабления обшивки отверстиями.
Проверка прочности сжатой обшивки производится при действии Рэи Рр.
Рис. 14.10 и 14.11 поясняют НДС сжатой панели и содержат механические характеристики ее элементов.
Рис. 14.11. Схематизированные диаграммы силовых элементов сжатой панели крыла
1- поясов; 2 – стрингеров; 3 - обшивки
Критические напряжения элементов панели следующие:
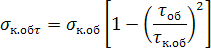 (14.5)
(14.5)
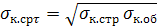
Здесь критические напряжения σк.об и τк.об соответствуют раздельному действию σи τ и определяются для участка между стрингерами и нервюрами, как для свободно опертой пластины.
При проверке прочности на Ррвводится характеристика τроб, а при проверке на Рэ — τэоб = τр/f.
Дюралюминиевая обшивка толщиной 1,5...2мм при обычном стрингерном подкреплении не должна терять устойчивость до нагрузки Рэ.
Условие обеспечения ее прочности: σэоб ≤ σк.обτэ.
Условие прочности такой обшивки при действии Рр соответствует требованию обеспечения устойчивости всей панели в целом (даже, если обшивка между стрингерами устойчивость потеряла): σроб ≤ σк.ср τ.
Дюралюминиевая обшивка толщиной более 2мм не должна терять устойчивость до нагрузки Рр, так как при потере устойчивости она разрушается. Условие обеспечения прочности такой обшивки σроб ≤ σк.об.τp.
Такое же требование предъявляется к прочности обшивки баков.
Стрингерное подкрепление обшивки самое распространенное.
Рациональность принятого сочетания стрингеров и обшивки можно оценить удельной прочностью панели подкрепленной обшивки при сжатии σк.пан/ρ.
Если панель состоит из тстрингеров, имеющих площадь fстp и шаг tстр. и обшивки шириной В = mtстpи толщиной δоб, то критическая сила панели равна
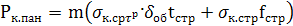 (14.6)
(14.6)
Редукционный коэффициент подкрепленной обшивки (относительно стрингеров)
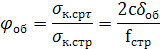 (14.7)
(14.7)
где 2с ≈ (25... 30) δоб — ширина участка обшивки, работающего совместно со стрингером, учитываемая при определении σк.стр при общей потере устойчивости.
Приведенная толщина обшивки со стрингерным подкреплением
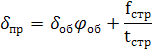 (14.8)
(14.8)
Очевидно, что максимальное значение критической нагрузки на панель Рк.пан получается при σк.об = σк.стр. Выполнение этого условия определяется формой стрингера, соотношением их площади fстр, шага tи толщины обшивки.
Обычно 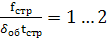 . (14.9)
. (14.9)
Двухпоясная балка
Приближенный расчет крыла, фюзеляжа, нервюр и других частей на изгиб основывается на принятии в качестве расчетной схемы модели двухпоясной балки, которая имеет наиболее выгодную в массовом отношении форму сечения балки (при работе на изгиб).
Расчет конструкции как двухпоясной балки значительно упрощает вычислительные операции.
Распределение напряжений в сечении двутавровой балки показано на рис. 14.12, а. Для ее модели — двухпоясной балки (рис. 14.12, б) площадь стенки
Fст = Hδст. (14.9)
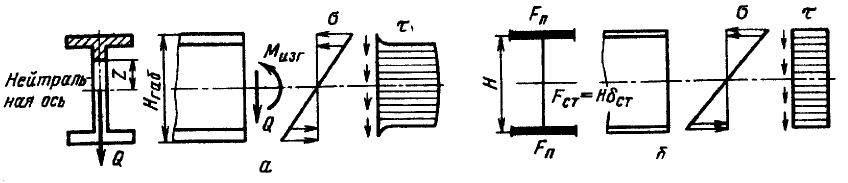 Момент инерции сечения (соб-ственными момен-тами инерции поясов и стенки пренебре гаем). Рис. 14.12 К расчету двутавровой балки равен.
Момент инерции сечения (соб-ственными момен-тами инерции поясов и стенки пренебре гаем). Рис. 14.12 К расчету двутавровой балки равен.
а -распределение нормальных и касательных J = FпH2/2. (14.10)
напряжений в сечении действительной балки;
б - двухпоясная балка.
Усилие в поясе Р = Мизг /Н, а напряжение в нем равно
σ = P/Fn = Mизг /(Fn·H). (14.11)
Здесь Н - рабочая высота, определяемая обычно как расстояние между ЦТ площадей сечений поясов. Чем больше разнесены пояса, чем они тоньше, тем их напряженное состояние ближе к чистому растяжению и сжатию.
При работе балки в упругой области напряжения в ней обусловлены удалением от нейтральной оси. Максимальное напряжение пояса σmахотличается от среднего σ= P/Fnвследствие отличия габаритной высоты балки Нгаб от Н.
Как следует из рис. 14.12 а,
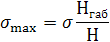 (14.12)
(14.12)
При работе пояса в пластической области распределение напряжений в нем можно считать равномерным.
Считая, что поперечная сила воспринимается только участком стенки с высотой Н в виде равномерно распределенных напряжений, получим
τ=Q/Fст (14.13)
Непараллельность поясов.
Рассмотрим влияние непараллельности поясов двухпоясной балки, характеризующейся углом α, на усилия в элементах сечения (рис. 4.13, а).
Обычно в самолетных конструкциях этот угол мал отсюда
r = Н/α. (14.14)
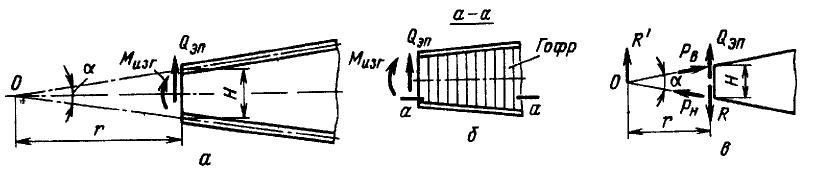
Рис. 14.13. Влияние непараллельности поясов двухпоясной балки на
распределение Мизг и Q между ее элементами (а, б, в)
Усилия Qи Мизг действуют со стороны левой отсеченной части балки на рассматриваемую правую часть.
Для учета влияния непараллельности поясов на распределение Мизги Qмежду элементами балки примем, как и для двухпоясной балки с параллельными поясами, что пояса могут воспринимать силы только вдоль своей оси, а стенка воспринимает силы, параллельные сечению.
Свойство стенки воспринимать только силы, параллельные сечению, можно пояснить на примере тонкой стенки из гофра с гребнями волн, параллельными сечению (рис. 14.13, б). Стенка неоказывает сопротивления силам, направленным вдоль оси балки.
В соответствии с данными допущениями поперечная сила и изгибающий момент распределяются между стенкой и поясами так, как показано на рис. 14.13, в.
Поперечная сила Qпередается непосредственно на стенку, а изгибающий момент Мизгпередаетсяв виде пары сил Rи R'
(R' =`Рв -`Рн),которые распределяются в соответствии с возможностью конструкции воспринимать их.
Равнодействующая сил Рв и Рн, воспринимаемых верхним и нижним поясами должна проходить через точку О пересечения их осей. Это определяет место одной из сил пары (R'), другая сила (R) должна лежать в плоскости сечения:
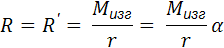 (14.15)
(14.15)
Силу R, приложенную в плоскости стенки, объединим с силой Q. Полученную в результате суммирования силу можно назвать приведенной поперечной силой (в отличие от поперечной силы, взятой из расчета поперечных сил или из эпюры Qэп):
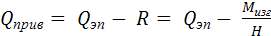 α. (14.16)
α. (14.16)
Сила R', приложенная в точке О, вызовет только продольные усилия в поясах. Значения их можно найти из треугольника равновесия сил Рв, Рн и R'. Учитывая небольшую величину угла α,
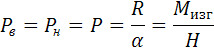 (14.17)
(14.17)
Следовательно, усилия в данном случае приближенно выражаются той же формулой, что и для балки с параллельными поясами.
Дата добавления: 2015-12-22; просмотров: 2280;
