Частные случаи политропных процессов
Как следует из определения показателя политропы (3.7), он может принимать значения от –∞ до +∞. Чаще всего на практике имеют дело с четырьмя частными случаями политропных процессов. Рассмотрим подробно каждый из них.
А) Изохорный процесс
По определению изохорным (изохорическим) процессом называется процесс, в течение которого поддерживается постоянным объём системы, т.е. уравнение изохорного процесса можно записать в виде
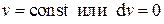 . (3.17)
. (3.17)
Показатель политропы для изохорного процесса может быть найден из соотношения между давлениями и объёмами в политропном процессе. В самом деле, из (3.12) имеем
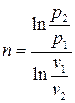 . (3.18)
. (3.18)
Отсюда находим для изохорного процесса 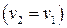
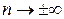 . (3.19)
. (3.19)
Тогда термодинамический расчёт изохорного процесса сведётся к использованию формул для политропного процесса, в которых следует переходить к пределу 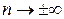 . Получаем
. Получаем
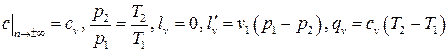 . (3.20)
. (3.20)
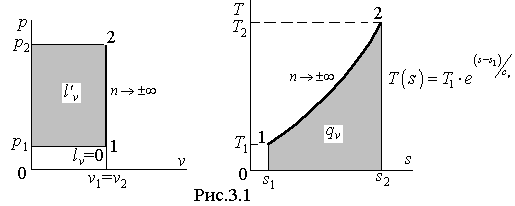
Изображение изохорного процесса в термодинамических диаграммах показано на рис.3.1.
 |
Б) Изобарный процесс
Изобарным (изобарическим) называется процесс при постоянном давлении, т.е. 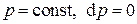 . Из (3.18) находим показатель политропы изобарного процесса:
. Из (3.18) находим показатель политропы изобарного процесса: 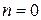 . Тогда, полагая во всех формулах для политропного процесса
. Тогда, полагая во всех формулах для политропного процесса 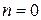 , получаем
, получаем
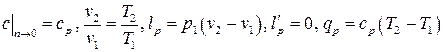 . (3.21)
. (3.21)
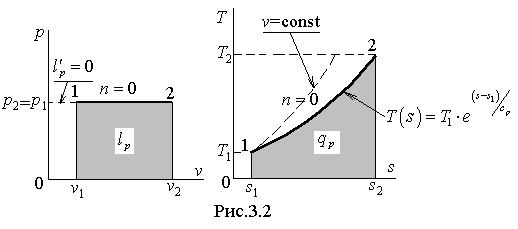
На рис.3.2 показано изображение изобарного процесса в термодинамических диаграммах.
На диаграмме 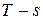 пунктиром показан также изохорный процесс, который изображается экспоненциальной кривой бόльшей крутизны, что следует из сравнения производных
пунктиром показан также изохорный процесс, который изображается экспоненциальной кривой бόльшей крутизны, что следует из сравнения производных
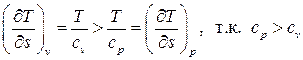 . (3.22)
. (3.22)
 |
В) Изотермический процесс
Изотермическим называется процесс, в течение которого поддерживается постоянной температура системы. Это возможно, если система, оболочка которой обладает идеальной теплопроводимостью, помещена в термостат, т.е. в среду с постоянной температурой. Уравнение изотермического процесса следующее:
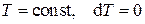 . (3.23)
. (3.23)
Показатель политропы изотермического процесса может быть найден из второго соотношения в (3.12), которое даёт
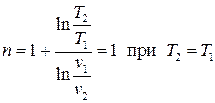 . (3.24)
. (3.24)
Тогда из соотношений между параметрами в политропном процессе (3.12) получаем
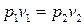 , (3.25)
, (3.25)
т.е., как и следовало ожидать, известный закон Бойля – Мариотта.
Теплоёмкость изотермического процесса оказывается равной бесконечности, что следует из (3.11) при стремлении 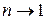 . Этот результат приводит к неопределённости типа
. Этот результат приводит к неопределённости типа 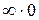 при вычислении количества теплоты в изотермическом процессе по стандартной формуле (3.13). Эта неопределённость легко устраняется при использовании I закона термодинамики. В самом деле, для изотермического процесса
при вычислении количества теплоты в изотермическом процессе по стандартной формуле (3.13). Эта неопределённость легко устраняется при использовании I закона термодинамики. В самом деле, для изотермического процесса
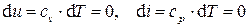 , (3.26)
, (3.26)
откуда имеем для изотермического процесса идеального газа
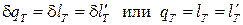 . (3.27)
. (3.27)
Работа изменения объёма в изотермическом процессе (или полезная внешняя работа) может быть вычислена после взятия предела второго выражения в (3.15)
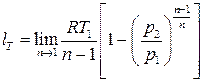 ,
,
однако можно поступить проще, используя определение для работы (3.14), положив в нём n=1, т.е.
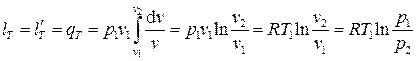 . (3.28)
. (3.28)
Изменение энтропии в изотермическом процессе находится из определения (3.2), откуда имеем
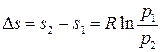 . (3.29)
. (3.29)
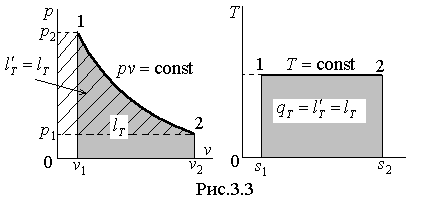
В координатах p - v изотермический процесс изображается равнобочной гиперболой, описываемой уравнением 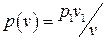 , а в T - s – прямой линией T=const (рис.3.3).
, а в T - s – прямой линией T=const (рис.3.3).
 |
Г) Адиабатический процесс
По определению адиабатическим (адиабатным) процессом называется процесс без теплообмена, т.е. 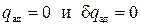 . Осуществить его можно, поместив систему в нетеплопроводную оболочку. Из определения количества теплоты в политропном процессе (3.13) следует, что теплоёмкость адиабатного процесса равна нулю (сад=0), а из (3.2) находим, что в обратимом адиабатическом процессе остаётся постоянной энтропия, т.е. уравнение адиабатического процесса может быть записано в виде
. Осуществить его можно, поместив систему в нетеплопроводную оболочку. Из определения количества теплоты в политропном процессе (3.13) следует, что теплоёмкость адиабатного процесса равна нулю (сад=0), а из (3.2) находим, что в обратимом адиабатическом процессе остаётся постоянной энтропия, т.е. уравнение адиабатического процесса может быть записано в виде
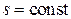 . (3.30)
. (3.30)
Из определения теплоёмкости политропного процесса (3.11) находим значение показателя политропы для адиабатического процесса:
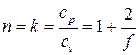 . (3.31)
. (3.31)
В переменных (p,v) уравнение адиабатного процесса имеет вид
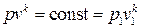 . (3.32)
. (3.32)
Работа в адиабатном процессе, как следует из I начала термодинамики, осуществляется за счёт уменьшения внутренней энергии системы и может быть вычислена по формулам (3.15) с заменой n→k:
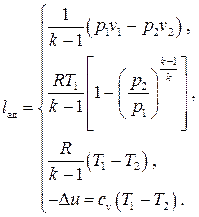 (3.33)
(3.33)
Полезная внешняя работа адиабатического процесса в k раз больше работы изменения объёма и совершается за счёт уменьшения энтальпии системы: 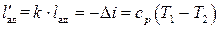 . (3.34)
. (3.34)
Изображение обратимого адиабатического процесса в термодинамических диаграммах показано на рис.3.4.
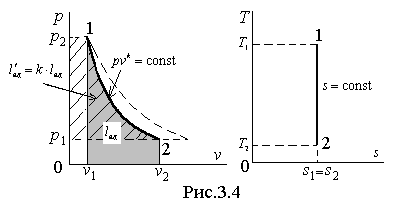 |
Пунктирной линией на диаграмме p - v показан изотермический процесс, который изображается более пологой кривой, нежели адиабата. В самом деле, сравнивая производные зависимостей давления от объёма для адиабаты и изотермы, получаем
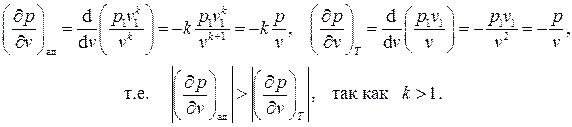
Дата добавления: 2015-12-22; просмотров: 1219;
