Для обозначений на рисунке получаем
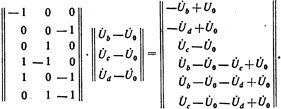
В результате умножения получена матрица, элементами которой являются падения напряжения в ветвях. Следовательно, при совмещении базисного и балансирующего узлов произведение

или, обозначая
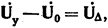

При несовпадении базисного и балансирующего узлов для установления связи между матрицами 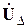 и
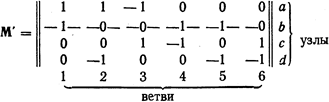
и 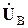 должна быть предварительно составлена матрица M’. Эта матрица может быть получена из первой матрицы соединений, составленной с учетом всех узлов направленного графа схемы (включая балансирующий и базисный), путем вычеркивания строки, отвечающей базисному узлу. В рассмотренном примере направленного графа такая матрица при выборе в качестве базисного узла b
должна быть предварительно составлена матрица M’. Эта матрица может быть получена из первой матрицы соединений, составленной с учетом всех узлов направленного графа схемы (включая балансирующий и базисный), путем вычеркивания строки, отвечающей базисному узлу. В рассмотренном примере направленного графа такая матрица при выборе в качестве базисного узла b
или
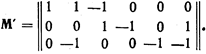
Умножая транспонированную матрицу М' на матрицу 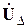 , находим
, находим
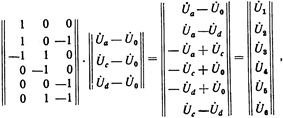
или, в обобщенной форме,

Последнее выражение (5-13) имеет общий характер, тогда как  отвечает частному случаю. Поэтому в дальнейшем уравнение, устанавливающее связь между матрицами
отвечает частному случаю. Поэтому в дальнейшем уравнение, устанавливающее связь между матрицами 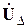 и
и 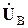 , записывается в форме в последней форме (5-13). Из предыдущих выражений (5-6) и (5-13) следует, что
, записывается в форме в последней форме (5-13). Из предыдущих выражений (5-6) и (5-13) следует, что
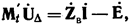
или, поскольку матрица сопротивлений ветвей 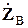 квадратная и неособенная,
квадратная и неособенная,
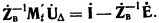
Умножая правую и левую части полученного выражения на матрицу М, получаем
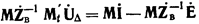
или,
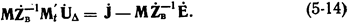
В правую часть этого матричного уравнения входят матрицы известных величин, являющихся исходными данными для расчета параметров режима схемы. В левой части этого уравнения имеется произведение трех матриц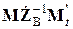 , результатом которого является некоторая матрица, имеющая размерность проводимости. Принимая
, результатом которого является некоторая матрица, имеющая размерность проводимости. Принимая

имеем из (5-14)

Матрицу 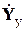 называют матрицей узловых проводимостей, а уравнение —узловым уравнением, записанным с использованием матрицы узловых проводимостей.
называют матрицей узловых проводимостей, а уравнение —узловым уравнением, записанным с использованием матрицы узловых проводимостей.
Матрица узловых проводимостей имеет число строк и столбцов, равное числу узлов схемы без одного — базисного.
Квадратная матрица 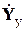 , неособенная, поэтому можно получить из (5-14)
, неособенная, поэтому можно получить из (5-14)
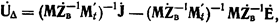
или, учитывая принятые обозначения (5-15),
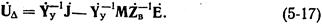
Элементы матрицы 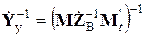 имеют размерность сопротивления, поэтому принимают обозначение
имеют размерность сопротивления, поэтому принимают обозначение
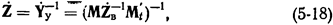
причем матрицу 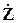 называют матрицей узловых сопротивлений.
называют матрицей узловых сопротивлений.
С учетом этого уравнение (5-17) записывается

Это уравнение называют узловым уравнением, записанным с использованием матрицы узловых сопротивлений. Из него, принимая во внимание, что 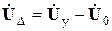 , можно получить матрицу искомых узловых напряжений
, можно получить матрицу искомых узловых напряжений
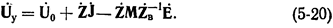
Расчеты токораспределения с помощью метода узловых напряжений
Число уравнений при определении токораспределения можно уменьшить, выразив искомые токи через падения напряжения в ветвях рассчитываемой схемы. Падения напряжений находятся как разность напряжений в узлах, что и определило, как известно, название метода расчета. Число узлов в любой схеме всегда меньше числа ветвей в ней, поэтому вычисление напряжений в узлах является всегда более простой задачей, нежели непосредственное определение токов прямым методом, предусматривающим выполнение операций с матрицами, имеющими порядок, равный числу ветвей в схеме.
Связь токов в ветвях с напряжениями в узлах определяется в матричной форме выражением
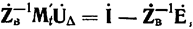
откуда следует, что
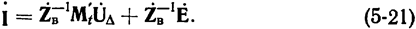
Эта формула требует для определения искомых токов предварительного вычисления матриц 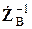 и
и 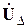 .
.
Структура обращенной матрицы сопротивлений ветвей на примере кольцевой сети с тремя ветвями в расчетной схеме:
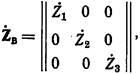
 .
.
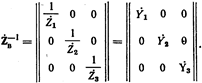
Элементами обобщенной матрицы сопротивлений ветвей являются проводимости этих ветвей, являющиеся обратными величинами элементов обращаемой матрицы. Это справедливо для любой диагональной матрицы.
Вычисление матрицы 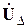 требует решения узлового уравнения, что связано с необходимостью обращения матрицы узловых проводимостей. В сложных сетях с большим количеством узлов в расчетных схемах выполнение этой операции может быть сопряжено с большими трудностями. Известен ряд предложений по преодолению возникающих затруднений. Некоторые из них предусматривают предварительные преобразования матрицы узловых проводимостей, облегчающие ее обращение. Другие основаны на предварительных упрощениях расчетной схемы, при которых удается уменьшить число узлов в ней. Наибольшее же распространение получил способ решения узлового уравнения методом итерации (последовательных приближений) при записи этого уравнения с использованием матрицы узловых проводимостей.
требует решения узлового уравнения, что связано с необходимостью обращения матрицы узловых проводимостей. В сложных сетях с большим количеством узлов в расчетных схемах выполнение этой операции может быть сопряжено с большими трудностями. Известен ряд предложений по преодолению возникающих затруднений. Некоторые из них предусматривают предварительные преобразования матрицы узловых проводимостей, облегчающие ее обращение. Другие основаны на предварительных упрощениях расчетной схемы, при которых удается уменьшить число узлов в ней. Наибольшее же распространение получил способ решения узлового уравнения методом итерации (последовательных приближений) при записи этого уравнения с использованием матрицы узловых проводимостей.
Матрица узловых проводимостей 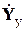 определяется как произведение трех матриц (выражение 5-15
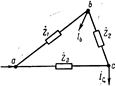
определяется как произведение трех матриц (выражение 5-15 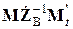 ). Выполним эту операцию применительно к сети, схема замещения которой показана на рис. а, а ее направленный граф на рис. б.
). Выполним эту операцию применительно к сети, схема замещения которой показана на рис. а, а ее направленный граф на рис. б.
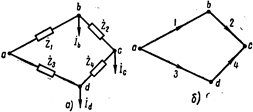
Принимая за балансирующий узел а, будем иметь

При совмещении базисного и балансирующего узлов
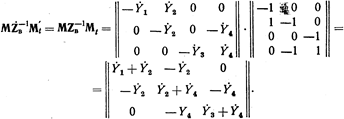
Каждая строка полученной матрицы отвечает одному узлу, так же как и каждый ее столбец. Следовательно,
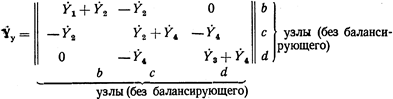
На главной диагонали матрицы  расположены элементы, представляющие сумму проводимостей ветвей, связанных с одним из узлов схемы. Другими элементами этой матрицы являются проводимости ветвей с обратным знаком между узлами, которым отвечают соответствующие столбцы и строки матрицы.
расположены элементы, представляющие сумму проводимостей ветвей, связанных с одним из узлов схемы. Другими элементами этой матрицы являются проводимости ветвей с обратным знаком между узлами, которым отвечают соответствующие столбцы и строки матрицы.
При несовпадении базисного и балансирующего узлов строки матрицы 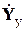 отвечают также всем узлам, кроме балансирующего, тогда как столбцы этой матрицы соответствуют всем узлам, включая балансирующий, но без базисного узла. Если в рассматриваемом примере за балансирующий по-прежнему считать узел а, а за базисный — узел b, то в результате перемножения матриц можно получить
отвечают также всем узлам, кроме балансирующего, тогда как столбцы этой матрицы соответствуют всем узлам, включая балансирующий, но без базисного узла. Если в рассматриваемом примере за балансирующий по-прежнему считать узел а, а за базисный — узел b, то в результате перемножения матриц можно получить
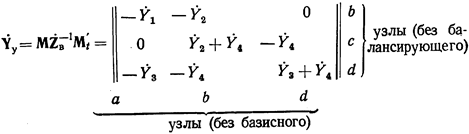 внизу не b, а c стоит.
внизу не b, а c стоит.
В этом случае на главной диагонали при совпадении индексов строк и столбцов опять расположены элементы, являющиеся суммой проводимостей ветвей, связанных с одним из узлов схемы. Все остальные элементы матрицы представляют собой взятые с обратным знаком проводимости ветвей между узлами, которые отвечают пересекающимся в данном элементе строкам и столбцам матрицы.
Непосредственным умножением матриц 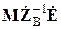 можно убедиться, что результатом его является столбцовая матрица. Каждая строка этой матрицы представляет собой сумму произведений вида
можно убедиться, что результатом его является столбцовая матрица. Каждая строка этой матрицы представляет собой сумму произведений вида 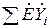 , где
, где 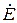 — э.д.с. в ветви, связанной с узлом, которому отвечает строка матрицы,
— э.д.с. в ветви, связанной с узлом, которому отвечает строка матрицы, 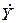 — проводимость этой ветви. Операция суммирования производится для всех ветвей, сходящихся в данном узле. При этом э.д.с. принимается положительной, если она направлена от узла, и отрицательной, если она направлена к узлу.
— проводимость этой ветви. Операция суммирования производится для всех ветвей, сходящихся в данном узле. При этом э.д.с. принимается положительной, если она направлена от узла, и отрицательной, если она направлена к узлу.
Правила составления матрицы узловых проводимостей 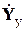 и матрицы
и матрицы 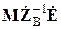 непосредственно по схеме замещения сети без предварительных операций с матрицами соединений позволяют упростить подготовку к непосредственному расчету режима сети.
непосредственно по схеме замещения сети без предварительных операций с матрицами соединений позволяют упростить подготовку к непосредственному расчету режима сети.
Итерационные методы решения узлового и контурного уравнении
Непосредственно определить матрицы узловых напряжений и контурных токов можно на основании узлового и контурного уравнений в формах, требующих вычисления обратных матриц. В первом случае приходится обращать матрицу узловых проводимостей, во втором—матрицу контурных сопротивлений. При расчетах сложных сетей с большим числом узлов и независимых контуров обращение матриц высокого порядка может вызвать значительные затруднения.
Применяя метод итераций, можно упростить решение узловых и контурных уравнений. При этом уравнения записываются в форме, не предусматривающей вычисления обратных матриц:
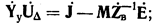 (32)
(32)
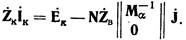 (33)
(33)
Эти матричные уравнения по своей структуре полностью идентичны. В левых их частях имеются произведения квадратных матриц некоторых комплексных коэффициентов на столбцовые матрицы искомых величин. Правые части уравнений содержат матрицы известных величин. Идентичность уравнений позволяет использовать для них одни и те же методы решения.
Рассмотрим два способа решения уравнений методом итераций. Первый — на примере и при обозначениях узлового уравнения, а второй—на примере и при обозначениях контурного уравнения. Оба метода справедливы для обоих из рассматриваемых уравнений.
Итерационный метод предполагает получение решения задачи как результат последовательного приближения к нему после ряда однотипных расчетов. При этом исходными данными являются произвольно принятые значения искомых величин. Применительно к узловому уравнению такими данными, принимаемыми на начальной стадии расчета (нулевая итерация), являются напряжения в (п—1) узле схемы, образующие столбцевую матрицу 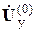 . Матрица
. Матрица 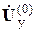 в общем случае не будет удовлетворять уравнению (32) в силу произвольного характера выбора напряжений, составляющих эту матрицу. Следовательно, нулевая итерация в лучшем случае позволяет получить лишь достаточно близкое приближение напряжений в узлах к фактическим значениям.
в общем случае не будет удовлетворять уравнению (32) в силу произвольного характера выбора напряжений, составляющих эту матрицу. Следовательно, нулевая итерация в лучшем случае позволяет получить лишь достаточно близкое приближение напряжений в узлах к фактическим значениям.
Правые части уравнений (32) в той или иной степени будут отличаться от левых. Для удовлетворения этих уравнений необходимо внести поправки в принятые на стадии нулевой итерации напряжения в узлах схемы, выполнив расчеты следующей — первой — итерации. Пусть схема имеет четыре узла. Один из этих узлов принят базисным, поэтому число искомых неизвестных в рассматриваемом примере будет равно трем. При  имеем (из уравнения (32))
имеем (из уравнения (32))
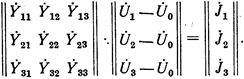 (34)
(34)
Этому матричному уравнению (34) соответствует система алгебраических уравнений:
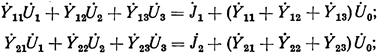
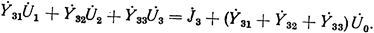
При произвольно принятых напряжениях 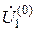 ,
, 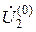 и
и 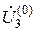 каждое из уравнений записанной системы может быть удовлетворено, если в левую часть их будет внесена некоторая поправка. Рассматриваемый способ простой итерации предусматривает внесение таких поправок лишь к одному из неизвестных, входящих в уравнение. При этом
каждое из уравнений записанной системы может быть удовлетворено, если в левую часть их будет внесена некоторая поправка. Рассматриваемый способ простой итерации предусматривает внесение таких поправок лишь к одному из неизвестных, входящих в уравнение. При этом
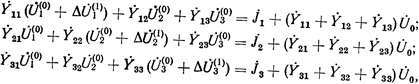
откуда, рассматривая поправки 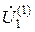 ,
, 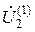 и
и 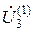 в качестве неизвестных, можно найти
в качестве неизвестных, можно найти
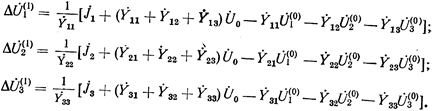
Совокупность поправок, входящих в левые части записанных выражений, образует столбцовую матрицу 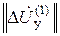 , а совокупность членов в квадратных скобках правых частей образует алгебраическую сумму матриц
, а совокупность членов в квадратных скобках правых частей образует алгебраическую сумму матриц 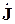 ,
, 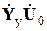 и
и 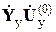 .
.
Выполняя операцию умножения матриц, находим:
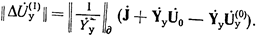 (35)
(35)
В общем случае 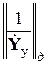 —диагональная матрица, элементами которой служат обратные величины узловых проводимостей, расположенных на главной диагонали матрицы узловых проводимостей.
—диагональная матрица, элементами которой служат обратные величины узловых проводимостей, расположенных на главной диагонали матрицы узловых проводимостей.
В рассматриваемом примере
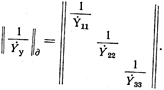
При наличии э.д.с. в ветвях схемы в правую часть матричного уравнения для  (35) должен войти член
(35) должен войти член  , имеющийся в правой части узлового уравнения (32). Следовательно, в общем случае
, имеющийся в правой части узлового уравнения (32). Следовательно, в общем случае
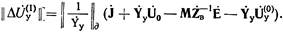 (36)
(36)
Поправки, найденные в соответствии с этим уравнением, позволяют удовлетворить каждое из узловых уравнений, входящих в систему, отвечающую матричному узловому уравнению. При введении поправок узловые напряжения
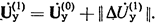
Однако эти напряжения не удовлетворяют всей системе в целом, поскольку каждая из поправок была найдена из условия удовлетворения лишь одного из уравнений этой системы. По этому необходимы дальнейшие уточнения узловых напряжений путем введения новых поправок. Матрица поправок второй итерации будет по структуре аналогична (36) с тем лишь различием, что для второй итерации исходными данными служат узловые напряжения, найденные при первой итерации, т.е.
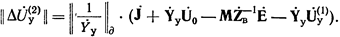 (36 а)
(36 а)
Сравнение (35) и (36 а) позволяет установить, что в оба эти выражения входит ряд общих членов. Поэтому, обозначая
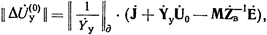
можно для поправок любой n-й итерации написать
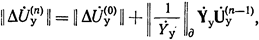 (37)
(37)
а также
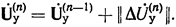 (38)
(38)
Если при переходе от одной итерации к другой матрица поправок уменьшается, то говорят, что итерационный процесс сходится. При этом на некоторой k-й итерации определяется матрица искомых узловых напряжений, удовлетворяющая узловому уравнению с заданной точностью. Признаком этого является удовлетворение неравенства
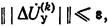
где e — матрица малых наперед заданных величин, характеризующих принятую точность расчета.
Возможно применение способа итерации и в других формах.
Нелинейные уравнения установившегося режима
Нелинейные уравнения узловых напряжений описывают установившийся режим электрической системы при задании нелинейных источников тока. В схеме замещения электрической системы нелинейным источникам тока соответствуют генераторы с заданной мощностью либо нагрузки потребителей, заданные статической характеристикой или постоянной мощностью. При заданной мощности нагрузки потребителя или генератора узловой ток задается в следующем виде:
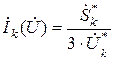 ; (_47)
; (_47)
где 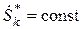 – сопряженная заданная мощность трех фаз k-го узла;
– сопряженная заданная мощность трех фаз k-го узла; 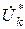 – сопряженный комплекс междуфазного напряжения k-го узла;
– сопряженный комплекс междуфазного напряжения k-го узла; 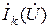 – нелинейный ток, зависящий от напряжения.
– нелинейный ток, зависящий от напряжения.
Если мощность нагрузки потребителя задана статической характеристикой, то нелинейный ток источника определяется следующим выражением:
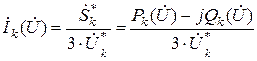 ; (_48)
; (_48)
где 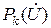 ,
, 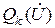 – статические характеристики активной и реактивной нагрузок k-го узла.
– статические характеристики активной и реактивной нагрузок k-го узла.
Нелинейные уравнения узловых напряжений при задании постоянной мощности нагрузки потребителей и генераторов в узлах для системы переменного тока из четырех узлов можно записать следующим образом:
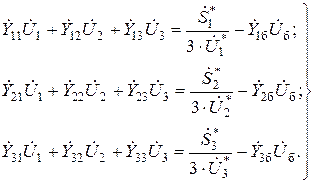 (_49)
(_49)
В матричной форме уравнения узловых напряжений имеют вид, аналогичный (9.20):
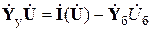 , (_50)
, (_50)
где 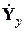 – комплексная матрица собственных и взаимных узловых проводимостей;
– комплексная матрица собственных и взаимных узловых проводимостей; 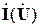 – вектор-столбец задающих токов, k-й элемент которого определяется выражением (_47);
– вектор-столбец задающих токов, k-й элемент которого определяется выражением (_47); 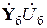 – вектор-столбец, k-й элемент которого равен
– вектор-столбец, k-й элемент которого равен 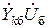 ;
; 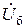 – заданное напряжение балансирующего узла.
– заданное напряжение балансирующего узла.
Каждое из записанных уравнений (_49) соответствует балансу комплексных токов в узле. Поэтому будем называть уравнения (_49) и (_50) уравнениями узловых напряжений в форме баланса токов. Система из трех комплексных уравнений узловых напряжений может быть заменена системой из шести действительных уравнений. Три действительных уравнения соответствуют балансу активных токов в узлах, а три – балансу реактивных токов.
Уравнения (_49) записаны для трех независимых узлов, в каждом из которых заданы Р и Q нагрузки. В систему (_49) не входит уравнение балансирующего (четвертого) узла. Уравнение баланса тока для балансирующего узла является следствием соответствующих уравнений для трех независимых узлов. Матрица производных системы уравнений, записанной для всех узлов, включая балансирующий, вырождена. Именно этим объясняется необходимость введения балансирующего узла, уравнение которого не включается в систему независимых нелинейных уравнений установившегося режима.
Если один из узлов—балансирующий по реактивной мощности, то его уравнение баланса реактивных мощностей (или токов) не входит в число независимых уравнений узловых напряжений. В общем случае может быть не один, а несколько балансирующих узлов. После решения системы независимых уравнений все Рг и Qг для балансирующих узлов и Qг для балансирующих по Q узлов определяются из уравнений баланса активных и реактивных токов для этих узлов, не входящих в число независимых уравнений узловых напряжений.
Уравнения узловых напряжений часто используются в форме баланса мощности, которые можно получить, если каждое уравнение баланса токов (_49) умножить на сопряженный комплекс напряжения соответствующего узла. Узловые уравнения баланса мощности для системы переменного тока из четырех узлов можно записать следующим образом:
 (_51)
(_51)
Эту систему можно записать в матричной форме следующим образом:
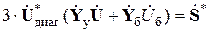 , (_52)
, (_52)
где 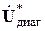 – диагональная матрица, k-й диагональный элемент которой равен сопряженному комплексу напряжения k-го узла;
– диагональная матрица, k-й диагональный элемент которой равен сопряженному комплексу напряжения k-го узла; 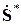 – вектор-столбец сопряженных мощностей в узлах, k-й элемент которого равен заданной сопряженной мощности k-го узла.
– вектор-столбец сопряженных мощностей в узлах, k-й элемент которого равен заданной сопряженной мощности k-го узла.
Матричное уравнение узловых напряжений в форме баланса мощностей (_52) можно получить в результате умножения матричного уравнения баланса токов (_50) слева на диагональную матрицу 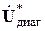 .
.
Чтобы получить алгебраическое уравнение баланса мощностей, необходимо уравнение баланса токов (_50) умножить на сопряженный комплекс напряжения узла.
При учете емкостных проводимостей линий собственная проводимость узла включает половины емкостных проводимостей всех линий, соединенных с данным узлом. При расчетах режимов на ЭВМ применяют уравнения узловых напряжений, учитывающие комплексные коэффициенты трансформации.
Дата добавления: 2015-12-22; просмотров: 1020;
